La lunette astronomique

La lunette astronomique
Objectifs : Le but de ce TP est comprendre le principe de formation de l’image au travers une lunette
astronomique puis de réaliser l’instrument à l’aide de deux lentilles convergentes.
I. Pré-requis
Deux personnes placées en P et Q observent un point B d’un objet. Les rayons lumineux issus de B et qui
arrivent en P et Q font un angle  qui dépend de la distance PQ mais aussi de la distance qui les sépare du
point B.
a) Que fait l’angle  si l’objet B est situé à plus grande distance ? (Voir schéma)
b) Si l’objet est maintenant à très très grande distance, que vaut l’angle  ?
c) Conclure : comment sont les rayons lumineux BP et BQ dans le cas d’un objet situé à l’infini ?
II. Réalisation de la maquette
La lunette pointe vers un astre situé à l’infini. Sur cet astre est repéré deux points A et B (A
situé au centre et B à la périphérie de l’astre)
On souhaite réaliser une lunette astronomique en utilisant deux lentilles L1 et L2 avec f’1>f’2. La
lentille placée du coté de l’objet est appelée l’objectif, celle placée devant l’œil est l’oculaire.
Les deux lentilles sont alignées et possèdent ainsi le même axe optique.
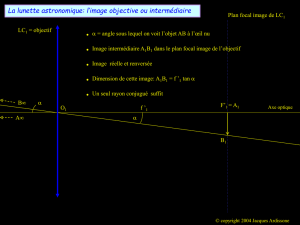
Dans un premier temps, on considère que la lentille L1 est l’objectif et L2 l’oculaire. (cas de la figure 1)
L’axe de la lunette (=axe optique des lentilles L1 et L2) est dirigé vers le point A, d’après le pré-requis, les
rayons lumineux issus de B arrivent parallèle entre eux sur la lentille mais font un angle  par rapport à l’axe
de la lunette (voir schéma de la figure 1) car le point B est excentré par rapport au point A.
L’objectif pointe en direction d’un objet AB éloigné (supposé à l’infini). Cet objet donne une image
intermédiaire A1B1 au travers l’objectif.
a) Le plan focal image de l’objectif est le plan passant par le foyer image de cette lentille et perpendiculaire
à l’axe optique. Tracer ce plan sur la figure 1.
b) Vérifier par une construction que l’image A1 B1 de cet objet AB situé à l’infini au travers l’objectif se
situe dans le plan focal image de cette lentille. (on complètera son schéma avec deux rayons particuliers
pour déterminer l’image B1 du point B).
Conclusion : Si un objet est ………………, son image se forme dans le …….. ………… de la lentille
B
B
P
Q
A
B

Pour une lunette astronomique, le foyer image de l’objectif coïncide avec le foyer objet de l’oculaire
c) Placer les foyers objet et image de l’oculaire sur la figure 1.
d) Quelle est la distance entre les deux lentilles? L’exprimer en fonction des distances focales f’1 et f’2
L’image A1B1 est maintenant un objet pour l’oculaire qui va donner une image A’B’.
e) Que peut-on prévoir concernant un objet qui se situe dans le plan focal d’une lentille ? (voir la
conclusion précédente avec le principe du retour inverse de la la lumière)
f) Construire l’image B’ du point B1 au travers l’oculaire.
g) Quel est l’intérêt de cette position pour l’œil ?
h) Sur la figure 2, on a permuté les 2 lentilles : la lentille L2 est l’objectif et L1 l’oculaire. Refaire le même
travail en cherchant la position de l’image intermédiaire A1B1 puis l’image définitive A’B’
i) Au travers une lunette astronomique, on souhaite regarder un astre sous le plus grand angle possible.
Parmi les deux lentilles, quelle est celle qui sera utilisé comme objectif ?
i) Donner le critère par rapport aux distances focales puis par rapport aux vergences des lentilles)
j) Construire la maquette qui va correspondre à ce critère. On donne pour la lentille A : VA=20  puis pour
la lentille B VB=10 
Soit ’ est l’angle sous lequel on voit l’objet à travers l’instrument. Placer sur le schéma l’angles ’
La grossissement de la lunette est donné par la relation : G=’/.
On admettra que pour des angles petits (inférieur à 10°) que tan  (rad). Exprimer puis calculer le
grossissement de la lunette simulée en fonction de f'1 et f'2.

Figure 1
Figure 2
L1
B
B
B
A
F1
O1
O2
L2
L2
B
B
B
A
F2
O2
O1
L1

MATERIEL
La lunette astronomique
Par groupe :
Nouveau banc d’optique
Lentille A, B et C
Réglet
Les 2 lunettes astronomiques