TD26_EM3_Complément_Effet Hall_Avec Corrigé

Exercice 5 du TD
Exercice 5 du TDExercice 5 du TD
Exercice 5 du TD :
: :
: C
CC
Capteur à Effet Hall
apteur à Effet Hallapteur à Effet Hall
apteur à Effet Hall
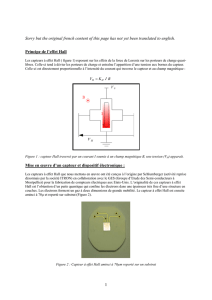
On considère une plaque rectangulaire d’épaisseur h, et de largeur b, représentée sur la figure suivante.
Elle est réalisée dans un semi-conducteur où la conduction électrique est assurée par des électrons mobiles
dont le nombre par unité de volume est n. La plaque est parcourue par un courant d’intensité I,
uniformément réparti sur la section de la plaque avec la densité volumique
x
J J e
= ⋅
(
0
J
>
).
Elle est alors placée dans un champ
magnétique uniforme
z
B B e
= ⋅
(
0
B
>
), crée
par des sources extérieures. Le champ
magnétique crée par le courant dans la plaque
est négligeable devant le champ extérieur, et
on suppose que le vecteur densité de courant
est toujours porté par l’axe (Ox) (circulation
permanente des e
-
).
1.
1. 1.
1. Champ électrique de Hall
Champ électrique de HallChamp électrique de Hall
Champ électrique de Hall
1.a) Exprimer le vecteur vitesse
v
des électrons dans la plaque en fonction de
J
, n et e en l’absence
de champ magnétique extérieur.
1.b) Lors de l’apparition d’un champ magnétique extérieur
B
, le courant est dévié et il va y avoir
accumulation de charges. Représenter sur un schéma ce phénomène.
1.c) En régime permanent, après que les charges se soient accumulées, le vecteur densité de courant
J
est forcément parallèle à (Ox) (sinon des charges sortiraient par les cotés de la plaque…), en
déduire que ces charges font apparaître un champ électrique dit de Hall :
1
H
E J B
ne
= ∧
.
1.d) Exprimer les composantes de ce champ de Hall
H
E
.
2.
2. 2.
2. Tension de Hall et mesure du champ
Tension de Hall et mesure du champTension de Hall et mesure du champ
Tension de Hall et mesure du champ magnétique
magnétique magnétique
magnétique
2.a) On considère 2 points M et N en vis-à-vis des faces 1 (x = -b/2) et 2 (x = +b/2). Calculer la
différence de potentiel entre ces deux points
H N M
U V V
= −
appelée tension de Hall
2.b) Montrer que
H
U
s’écrit
H
H
C
U I B
h
= ⋅ ⋅
, et exprimer la constante
H
C
. En quoi la mesure de
cette tension de Hall peut-elle être utile ?
2.c) AN : Pour l’antimoniure d’indium InSb,
6
375.10
H SI
C u
−
= ,
0,1
I A
=
,
0,3
h mm
=
et
88
H
U mV
=
. Calculer la norme du champ B, ainsi que la densité volumique n en
électrons par m
3
.
TD2
TD2TD2
TD2
6
66
6
–
––
–
EM3
EM3 EM3
EM3
–
––
–
C
CC
C
omplémen
omplémenomplémen
omplémen
t
tt
t
–
––
–
Effet HALL
Effet HALLEffet HALL
Effet HALL
h
b
z
x
B
y
M
N
O
Face 1
(Avant)
Face 2
(Arrière)
Courant I
Courant ICourant I
Courant I
Courant I
Courant ICourant I
Courant I
B

Exercice 5 du TD
Exercice 5 du TDExercice 5 du TD
Exercice 5 du TD :
: :
: Capteur à Effet Hall
Capteur à Effet HallCapteur à Effet Hall
Capteur à Effet Hall
1.
1. 1.
1. Champ électrique de Hall
Champ électrique de HallChamp électrique de Hall
Champ électrique de Hall
1.a) On a :
J nq v ne v
= ⋅ = − ⋅
1.b) Représentation de l’accumulation des charges en présence d’un champ magnétique extérieur
B
:
1.c) Les charges subissent une force magnétique de Lorentz
ext
F qv B
= ∧
qui les dévie, mais puisque
(
)
J Ox
, il y a forcément une autre force qui s’oppose à cette force magnétique. Il s’agit de
l’effet du champ de Hall crée par les charges :
+ = + ∧ =
_
0
élec Hall magn H
F F q E qv B
= − ∧ = ⇒= − ∧ = ∧
1
H all H H
F q v B q E A in si E v B J B
n e
1.d) Composantes du champ de Hall :
0 0
1 1
0 0
0 0
H
J
E JB
ne ne
B
= ∧ = −
H y
JB
E e
ne
−
⇒= ⋅
2.
2. 2.
2. T
TT
Tension de Hall et mesure du champ
ension de Hall et mesure du champension de Hall et mesure du champ
ension de Hall et mesure du champ magnétique
magnétique magnétique
magnétique
2.a) Tension de Hall :
N N
H N M H H H
M M
JB
U V V dV E dy E b U b
ne
= − = = − ⋅ = ⋅ = = ⋅
∫ ∫
(On utilise la relation entre potentiel et champ électrique
(
)
= − ⇒= − ⋅
E grad V dV E dl
)
2.b) Ainsi :
( )
×
= ⋅ = × ×
H
JB IB b
U b
ne b h ne
Et
= ⋅ ⋅ =
1
H
H H
C
U I B avec C
h ne
Utilité ?  On peut obtenir la valeur du champ
magnétique B par une mesure de
tension, il s’agit d’un capteur très
simple pour le champ magnétique.
2.c) AN :
3
6
0,3.10 0,125 704
375.10 0,1
H
H
h U
B mT
C I
−
−
⋅⋅
= = =
⋅⋅
Et
22 3
1
1,66.10 .m
H
n e
e C
− −
= =
⋅
TD2
TD2TD2
TD2
6
66
6
–
––
–
EM3
EM3 EM3
EM3
–
––
–
C
CC
C
omplément
omplémentomplément
omplément
–
––
–
Effet HALL
Effet HALLEffet HALL
Effet HALL
–
––
–
CORRIGE
CORRIGE CORRIGE
CORRIGE
V
VV
V
B
U
H
Mesure de la Tension de Hall
Mesure de la Tension de HallMesure de la Tension de Hall
Mesure de la Tension de Hall
Courant I
Courant ICourant I
Courant I
F
H
E
Champ de Hall
(du + vers le -)
Accumulation de
charges négatives
B
Courant I
Courant ICourant I
Courant I
Courant I
Courant ICourant I
Courant I
B
Accumulation de
charges positives
v
e
-
Vitesse d’un électron
du courant I
(Force Magnétique)