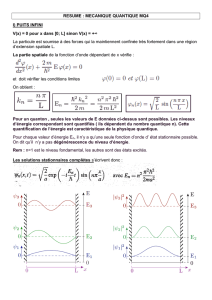
Les nitrures d`éléments III : des semiconducteurs III-V

28
Les nitrures d’éléments III
(GaN, AlN, InN et leurs
alliages) sont des semiconduc-
teurs aux propriétés remarquables.
La plus importante est sans conteste
leur bande interdite directe qui varie
de 1,9 eV pour InN à 3,4 eV pour
GaN, et atteint 6,2 eV pour AlN
(figure 1). Grâce aux concepts de
l’ingénierie de bande interdite déve-
loppés dans le cadre des semicon-
ducteurs III-V traditionnels (arsé-
niures, phosphures, antimoniures), il
est ainsi possible de couvrir entière-
ment la gamme spectrale visible,
mais aussi le domaine des ultravio-
lets A (320-400 nm) et B (280-320
nm). Ce point, complété par la très
forte stabilité du matériau de base
GaN, est à l’origine de la réalisation
industrielle de diodes électrolumi-
nescentes (DELs) bleues et vertes de
haute brillance, et de diodes laser
(DLs) émettant à 0,4 µm.
Après des débuts difficiles dans
les années 70, les nitrures d’éléments
III ont suscité un regain d’intérêt il y
a une dizaine d’années après que l’un
des verrous technologiques majeurs
– le dopage de type p – eut été réso-
lu. L’industrialisation de DELs
bleues et vertes a alors été très rapide
et a en fait précédé la compréhension
fine des phénomènes physiques mis
en jeu dans ces matériaux. Il est cer-
tain que la qualité médiocre du com-
posé de base GaN a sans aucun doute
accentué ce retard. Aujourd’hui, l’un
des objectifs majeurs de la recherche
fondamentale sur les nitrures
d’éléments III est d’identifier les
paramètres clefs qui gouvernent
l’émission de lumière dans les nano-
structures (puits ou boîtes quanti-
ques) utilisées comme couche active
des dispositifs électroluminescents.
Les deux problématiques récurrentes
concernent, d’une part, les effets de
polarisation liés à la structure hexa-
gonale de ces matériaux et, d’autre
part, les effets de localisations des
porteurs dans l’alliage GaInN.
POLARISATIONS SPONTANÉE ET PIÉZO-
ÉLECTRIQUE
L’une des spécificités des nitrures
d’éléments III, comparés aux autres
composés III-V tels que les arsé-
niures (GaAs par exemple), est leur
structure hexagonale de type wurtzi-
te. Dans la maille cristalline hexago-
nale, les barycentres des charges
positives et négatives ne coïncident
pas toujours, créant ainsi un
ensemble de dipôles orientés selon
une même direction. Il apparaît dès
lors dans le cristal une polarisation
macroscopique en l’absence de toute
contrainte externe (encadré 1). Cet
effet est bien connu dans les maté-
riaux ferroélectriques et est appelé
« polarisation spontanée ». Il est
important de souligner que ce phé-
nomène existe même dans le cas
d’une structure hexagonale parfaite
(c/a =√8/3). En revanche, il n’y a
pas de polarisation spontanée dans
Matériaux de basse dimensionnalité
Les nitrures d’éléments III : des
semiconducteurs III-V singuliers ?
Les nitrures d’éléments III sont des semiconducteurs remarquables car ils couvrent l’ensemble
du spectre visible ainsi que les ultraviolets A et B. Les dispositifs optoélectroniques à base de
nitrures présentent aujourd’hui des performances exceptionnelles, malgré une densité de
dislocations très élevée (> 108cm–2) et des champs électriques intrinsèques géants (plusieurs
MV/cm). Les différents phénomènes physiques mis en jeu dans ces matériaux sont illustrés
par les propriétés optiques de puits et de boîtes quantiques.
2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
0
1
2
3
4
5
6
AlP
InP
GaP
Si(111)
Bande interdite (eV)
Al
2
O
3
(0001)
SiC(0001)
AlAs
GaAs
InAs
AlSb
GaSb
InSb
MgS
ZnS
BeSe
MgSe
CdSe
ZnSe
AlN
InN
GaN
Parametre de maille (A)
0,6
1,2
0,4
0,3
0,2
Longueur d’onde (µm)
Figure 1 - Bande interdite de divers composés semiconducteurs en fonction de leur paramètre de maille.
Les nitrures d’éléments III couvrent un large domaine spectral qui s’étend du rouge (650 nm) à l’ultra-
violet (200 nm). Les substrats les plus couramment utilisés pour la croissance de ces matériaux sont le
saphir (Al2O3) et le carbure de silicium (SiC).
– Centre de recherche sur l’hétéroepitaxie
et ses applications (CRHEA), UPR 10
CNRS, bât. 5, rue Bernard Grégory,
Sophia Antipolis, 06560 Valbonne.

29
Matériaux de basse dimensionnalité
les semiconducteurs à phase cubique
en raison de leur symétrie.
Cependant, sous l’action d’une
contrainte bi-axiale, par exemple
dans le plan (111), la maille cristalli-
ne se déforme et brise la symétrie
cubique. Il apparaît alors une polari-
sation dans le cristal, orientée selon
l’axe polaire [111] (encadré 1). La
manifestation d’un champ électrique
sous l’action d’une contrainte est
appelée piézoélectricité. Une polari-
sation piézoélectrique orientée le
long de l’axe [0001] est aussi pré-
sente dans les semiconducteurs à
phase hexagonale lorsqu’une con-
trainte bi-axiale dans le plan (0001)
leur est appliquée. Dans un nitrure
d’éléments III, la polarisation totale
est la somme de la polarisation spon-
tanée (structure à l’équilibre) et
de la polarisation piézoélectrique si
contrainte il y a (encadré 1).
Nous discutons maintenant de
l’influence de la polarisation macro-
scopique sur les propriétés optiques
de nanostructures épitaxiées selon la
direction [0001]. Dans ce cas, l’axe
de polarisation est parallèle à l’axe
de croissance et perpendiculaire au
plan des couches. Si l’on juxtapose
deux matériaux nitrures Aet Bde
nature différente, comme GaN et
AlGaN, la discontinuité de polarisa-
tion macroscopique totale Pentre
les deux milieux se traduit à l’inter-
face A/Bpar un plan de charges
σ=P(A)–P(B). Ce plan de charge
crée à son tour dans le cristal un
champ électrique de module
E=σ/2εε0où εest la constante
diélectrique du matériau et ε0la per-
mittivité du vide. Dans un puits
quantique (B/A/B), les deux inter-
faces portent chacune un plan de
charge de même module mais de
signes opposés. Les champs élec-
triques créés par ces plans de
charges s’ajoutent dans le puits
quantique (E=σ/εε0)et s’annulent
en dehors, c’est-à-dire dans les bar-
rières (encadré 2).
L’importance des effets de polari-
sation dans les hétérostructures de
nitrures d’éléments III tient principa-
lement aux valeurs géantes du champ
électrique. A titre d’exemple, la théo-
rie prédit des champs électriques res-
pectivement de 10 MV/cm et
15 MV/cm dans les systèmes
GaN/AlN et InN/GaN. Ces valeurs
particulièrement élevées pour des
semiconducteurs sont issues de la
conjonction de trois facteurs. Tout
d’abord, les coefficients piézoélec-
triques dans ces matériaux sont très
grands, environ dix fois supérieurs à
ceux mesurés dans les semiconduc-
teurs III-V traditionnels. Ensuite, les
paramètres réticulaires entre les dif-
férents composés nitrures sont très
différents. Le désaccord de para-
mètre cristallin entre GaN et AlN est
2,5 %, et il atteint 11 % entre InN et
GaN. Toute hétérostructure nitrure
pseudomorphe (c’est-à-dire non
relaxée plastiquement par des dislo-
cations) est donc l’objet d’une
contrainte qui, combinée aux larges
coefficients piézoélectriques, engen-
dre de forts effets de polarisation.
Enfin, au champ piézoélectrique se
superpose le champ résultant de la
différence de polarisation spontanée
entre le matériau « puits » et le maté-
riau « barrière ». Bien que la polari-
sation spontanée dans les nitrures
d’éléments III soit beaucoup plus
faible que dans les matériaux ferro-
électriques, elle peut participer de
façon significative au champ élec-
trique interne. Dans un puits
quantique GaN/AlN par exemple,
le champ électrique théorique de
10 MV/cm vient pour moitié de la
différence de polarisation spontanée
entre GaN et AlN. En revanche, dans
le système GaInN/GaN, le champ
électrique interne est principalement
dû aux effets piézoélectriques, car la
différence de polarisation spontanée
entre GaN et InN est faible.
EFFET STARK CONFINÉ DANS LES PUITS
ET LES BOÎTES QUANTIQUES NITRURES
La présence d’un champ élec-
trique dans un puits quantique est
mise en évidence au travers d’expé-
riences de photoluminescence (PL).
Cette technique donne en effet accès
Figure 2 - Spectre de photoluminescence à basse température (10 K) de puits quantiques
GaN/Al0,17Ga0,83N de différentes largeurs. Pour des épaisseurs de puits supérieures à 3 nm, l’énergie
de transition est inférieure à celle du matériau GaN massif (3,48 eV). Cela est dû au champ électrique
interne provenant des polarisations spontanée et piézoélectrique qui déplace les transitions optiques
vers le rouge (effet Stark). En insert : énergie de transition expérimentale de puits quantiques
GaN/Al0,17Ga0,83N en fonction de la largeur du puits (carrés pleins). L’ajustement de ces valeurs par
un calcul de type fonction enveloppe (trait continu) permet de déduire un champ électrique interne de
710 kV/cm. La courbe en trait pointillé est le résultat du calcul à champ nul.

30
Encadré 1
POLARISATION SPONTANÉE ET PIÉZOÉLECTRIQUE
La symétrie de la structure cristalline d’un matériau a des
conséquences importantes sur ses propriétés de polarisation.
Dans le cas de composés fortement ioniques à phase hexago-
nale (wurtzite), tels les nitrures d’éléments III, la distribution
des densités électroniques autour des différents atomes fait
que les barycentres des charges positives et négatives ne coïn-
cident pas nécessairement. Cela donne lieu dans le cristal à
un ensemble de dipôles orientés suivant un même axe : le
matériau est le siège d’une polarisation macroscopique. Elle
prend l’appellation de polarisation spontanée, car ce phéno-
mène existe dans le cristal à l’équilibre en l’absence de toute
contrainte externe et ce, même pour une structure hexagonale
idéale (c/a =√8/3). Cette polarisation spontanée 
Psp ne se
manifeste pas dans le volume, mais aux interfaces du maté-
riau avec le vide ou avec un autre composé. Elle crée une
charge monopolaire à l’interface qui vaut 
Psp.nentre le maté-
riau et le vide, ou [
Psp(A)−
Psp(B)].nà l’interface entre
deux matériaux A et B (nvecteur unité normal à la surface).
Dans les nitrures d’éléments III, le vecteur polarisation 
Psp
est orienté suivant la direction [0001]. Il n’existe aujourd’hui
aucune mesure expérimentale absolue de la polarisation spon-
tanée dans les nitrures. Seul un calcul ab initio développé par
Bernardini et al. donne les valeurs numériques suivantes :
Psp =−0,081,−0,029 et –0,032C/m2pour AlN, GaN et InN,
respectivement.
coefficient piézoélectrique et les cij =c11,c12,c13,c33 sont
les constantes élastiques. Dans les nitrures d’éléments III, la
polarisation totale du milieu est donc la somme algébrique de
deux contributions, l’une existant à l’équilibre (la polarisation
spontanée), l’autre sous l’action d’une contrainte extérieure
(la polarisation piézoélectrique). Ces deux polarisations étant
de même nature physique, il est très difficile de déterminer
expérimentalement la contribution de chacune d’entre elles.
Psp ≠ 0
Structure GaN wurtzite
a l equilibre
Psp
[0001]
Ga
N
Ppz ≠ 0
Psp = 0
Structure cubique
a l equilibre
[111]
Ga
Ppz = 0
Ga
As
Structure cubique sous
contrainte bi-axiale
Psp = 0
As
Ppz
La polarisation spontanée n’existe pas dans les semiconduc-
teurs à phase cubique tel GaAs par raison de symétrie. En
revanche, l’action d’une contrainte bi-axiale exercée dans le
plan (111) brise la symétrie cubique et fait apparaître une
polarisation orientée suivant l’axe [111].
Ce phénomène est connu sous le nom de piézoélectricité. Une
polarisation piézoélectrique se manifeste aussi dans les semi-
conducteurs à phase wurtzite lorsque qu’une contrainte leur
est appliquée. Pour une contrainte bi-axiale exx dans le plan
(0001), le champ de polarisation piézoélectrique selon [0001]
s’écrit Ppz =2d31[c11 +c12 −2c2
13/c33]exx, où d31 est le
Ppz ≠ 0
Ga
N
Ppz
Structure wurtzite sous
contrainte bi-axiale
Psp ≠ 0
[0001]
Psp
POLARISATION SPONTANÉE
POLARISATION PIÉZOÉLECTRIQUE

31
Matériaux de basse dimensionnalité
Lorsqu’un champ électrique siège
dans un puits quantique, la chute de
potentiel associée dans les bandes de
conduction et de valence entraîne
une diminution de l’énergie de tran-
sition d’une quantité égale à −eLwE,
eétant la charge de l’électron, Lwla
largeur du puits quantique, et Ele
champ électrique. Ce décalage vers
le rouge des transitions optiques est
connu sous le nom d’effet Stark
confiné quantique (encadré 2).
Nous montrons en figure 2 le
spectre de PL à 10 K d’un échan-
tillon comportant plusieurs puits
quantiques GaN/Al0,17Ga0,83N éla-
boré par épitaxie sous jets molécu-
laires sur un substrat de saphir
[Al2O3(0001)]. L’épaisseur des dif-
férents puits varie de 1 nm à 8 nm, la
largeur des barrières AlGaN étant
constante (10 nm). Le puits le plus
étroit (Lw=1nm) émet à plus de
3,7 eV, soit bien au-dessus de la
bande interdite du matériau GaN
massif (3,48 eV à 10 K). Cela n’est
ni plus ni moins que la conséquence
du fort confinement quantique des
aux transitions électroniques fonda-
mentales d’une hétérostructure. Le
spectre de PL d’un puits quantique se
compose généralement d’un pic d’in-
tensité correspondant à l’émission de
photons lors de la transition des élec-
trons de leur niveau de base dans la
bande de conduction vers leur niveau
fondamental dans la bande de valen-
ce (encadré 2). L’énergie de transi-
tion dépend de la bande interdite du
matériau « puits », des masses effec-
tives des porteurs, de la largeur du
puits quantique et de la hauteur des
barrières de potentiel.
Encadré 2
EFFET STARK CONFINÉ QUANTIQUE
Un puits quantique est constitué d’une fine couche d’un maté-
riau A dans un matériau B dont la bande interdite est plus
grande. Si l’épaisseur de la couche A est suffisamment faible
(typiquement inférieure à 10 nm dans les nitrures d’éléments
III), les porteurs sont confinés et les niveaux d’énergie quanti-
fiés (traits pointillés). Ainsi, l’énergie de transition du niveau
fondamental dans la bande de conduction (BC) vers le niveau
fondamental dans la bande de valence (BV) est supérieure à
la bande interdite du matériau « puits ». Lorsque les maté-
riaux « puits » et « barrière » présentent une discontinuité de
polarisation macroscopique, des densités de charges (σ ) de
signes opposés apparaissent aux deux interfaces. Elles créent
à leur tour un champ électrique dans le puits qui entraîne un
effet Stark, c’est-à-dire un décalage vers le rouge des transi-
tions optiques (hν<hν). Dans le même temps, les porteurs
sont spatialement séparés comme l’indiquent leurs fonctions
d’onde (lignes continues grisées).
E = σ/εε0
E = 0
AlGaN AlGaN GaN
BC
BV
-σ+σ
hν
hν
Lw
Structure de bande de conduction (BC) et de bande de valence (BV) d’un puits quantique de largeur Lwavec et sans champ électrique E. Les traits
en pointillés correspondent aux énergies de confinement des électrons et des trous (niveau fondamental n=1), les traits pleins en grisé représen-
tent leurs fonctions d’onde. L’effet Stark confiné quantique dû au champ électrique E diminue l’énergie de transition du puits (hν<hν). La den-
sité de charge σ est fixée par la différence de polarisation macroscopique totale entre matériaux « puits » (GaN) et « barrière » (AlGaN).

32
porteurs dans les bandes de conduc-
tion et de valence lorsque le puits est
étroit. Quand l’épaisseur du puits
augmente, le confinement quantique
devient plus faible et l’énergie de
transition doit diminuer pour finale-
ment tendre vers celle du matériau
GaN massif (3,48 eV). Or, nous
constatons en figure 2 que l’énergie
de PL des puits quantiques de lar-
geur 4, 6, et 8 nm est inférieure à
3,48 eV. Cette caractéristique est la
signature d’un effet Stark confiné
quantique, conséquence d’un champ
électrique interne. Nous reportons en
insert dans la figure 2 les énergies de
transition expérimentales (carrés
pleins) des puits quantiques
GaN/Al0,17Ga0,83N en fonction de
leur largeur. L’ajustement de ces
données à partir d’un simple calcul
de type « fonction enveloppe » (trait
continu) permet d’évaluer le champ
électrique interne à 710 kV/cm (la
courbe en trait pointillé correspond
au calcul à champ nul).
Le champ électrique dépend de la
composition en aluminium des bar-
rières AlGaN. Ce paramètre joue à la
fois sur le champ piézoélectrique, la
contrainte étant fixée par la diffé-
rence de réseau cristallin entre GaN
et AlGaN, et sur la polarisation
spontanée (pour celle-ci, une simple
interpolation linéaire entre les
valeurs de GaN et AlN est utilisée
pour décrire l’alliage). Sont reportés
en figure 3 les spectres de PL de
quatre échantillons contenant cha-
cun quatre puits quantiques
GaN/AlxGa1−xN de largeur 1, 2, 3 et
4 nm (correspondant à 4, 8, 12, et
16 mono-couches moléculaires1), et
réalisés pour différentes composi-
tions d’aluminium. La figure 3
montre une dispersion en éventail
des énergies de transition lorsque la
composition en aluminium aug-
mente. Le décalage vers les hautes
énergies des pics de PL des puits les
plus étroits (1 et 2 nm) est la consé-
quence de l’augmentation du confi-
nement quantique des porteurs, alors
que le déplacement vers le rouge des
puits les plus larges (3 et 4 nm)
reflète l’accroissement du champ
électrique interne avec la composi-
tion en aluminium. Pour des bar-
rières en AlN, le champ atteint expé-
rimentalement 5 MV/cm. Cette
valeur très élevée conduit à un phé-
nomène assez singulier : les transi-
tions optiques des hétérostructures
quantiques GaN/AlN sont décalées
par effet Stark dans quasiment tout
le spectre visible, alors que les
bandes interdites de GaN et AlN
(respectivement 3,4 eV et 6,2 eV) ne
permettent a priori qu’une émission
dans l’ultraviolet. Ce point est illus-
tré en figure 4. Chaque tache de cou-
leur correspond à la photolumines-
cence à température ambiante d’un
plan de boîtes quantiques GaN dans
une matrice AlN. Lorsque la hau-
teur2des boîtes augmente, la lumi-
nescence varie du bleu à l’orange par
effet Stark géant. En combinant sur
un même échantillon des boîtes
quantiques de tailles judicieusement
choisies, l’émission résultante est
blanche en vertu de la loi d’addition
des couleurs (figure 4). Ce principe
est envisagé pour la production de
lumière blanche à partir de DELs de
nitrures, dont la zone active contien-
drait par exemple un émetteur bleu
et un émetteur jaune.
Figure 3 - Spectres de photoluminescence à basse température (10 K) d’une série d’échantillons com-
prenant 4 puits quantiques GaN de largeur 1, 2, 3 et 4 nm. La composition en aluminium dans les bar-
rières AlxGa1-xN varie de 8 à 27 %. L’énergie du puits le plus étroit (1 nm) augmente avec la composi-
tion, en raison de l’accroissement du confinement quantique alors que celle du puits le plus large (4 nm)
diminue à cause de l’effet dominant du champ électrique interne (effet Stark) qui augmente aussi avec
la composition.
1. Une mono-couche moléculaire de GaN équi-
vaut à un plan d’atomes de Ga plus un plan
d’atomes de N, soit 0,259 nm.
2. Dans le cas présent, la largeur des boîtes
quantiques est beaucoup plus importante que
leur hauteur si bien que la quantification a lieu
principalement selon cet axe. De ce fait, la hau-
teur d’une boîte quantique peut être assimilée à
la largeur d’un puits.