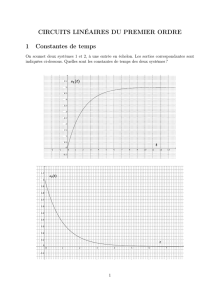
Charge et décharge d`un condensateur

1
t
U
E
0
E
Uc
Si au temps t=0 on ferme l’interrupteur, la
tension aux bornes du circuit passe brutalement
de 0 à E. c’est un échellon de tension
EXPERIENCES ET MESURES
A Charge d’un condensateur à courant constant
1- montage
Réaliser le montage suivant avec le générateur d’intensité et un
condensateur de 10000 µF (attention : celui-ci est polarisé) , un
voltmètre pour mesurer Uc, un ampèremètre réglé sur µA et un
interrupteur ouvert pour le moment.
Faire un essai pour voir si le condensateur se charge en fermant
l’interrupteur.
Ouvrir l’interrupteur, décharger le condensateur en faisant court-
circuit avec un fil.
2- Mesures :
A t=0, ouvrir l’interrupteur et déclencher le chronomètre. Faire une
mesure de Uc environ toutes les 10 s ou 15 s jusqu’à ce que le
condensateur soit chargé. Noter toutes les mesures dans un tableau.( t et Uc )
Relever également la valeur de i en µA
Refaire la même chose avec un condensateur de 4700µF
B charge d’un condensateur par un échelon de tension
Les mesures seront
réalisées grace à une interface d’acquisition reliée au logiciel SYNCHRONIE
1- Montage :
générateur sur une tension située en gros entre 4 et 6 V .
condensateur de 2µF ou 5µF , noter sa valeur.
potentiomètre = une résistance variable 0<R<10kΩréglage quelconque
interrupteur : ouvert pour le moment
Interface : relier les bornes du condensateur à l’interface.
2- Synchronie
Réglages : Paramètres : entréesA/D :
Entrée 0 ( nom :Uc, Unité : V; style : ++++ ; fenêtre : 1coché ; calibre -2 ; +6 )
Paramètres : acquisition : déclenchement source = entrée 0 Uc , niveau : 0.1 sens montant. ( cela permettra de
synchroniser la fermeture de l’interrupteur avec l’acquisition ce qui est impossible à la main)
200 mesures et intervalle entre 2 mesures : 200 µs
3- Acquisition
Appuyer sur la touche F10 puis juste après fermer l’interrupteur.
(Si la courbe de charge du condensateur n’est pas correct, ouvrir l’interrupteur, décharger le
condensateur par un fil de court-circuit, changer la valeur de R en tournant le potentiomètre et
recommencer.)
Ouvrir l’interrupteur, débrancher le potentiomètre en veillant à ne pas le dérégler et mesurer la valeur
de R avec un ohmmètre.
Noter aussi la valeur de E délivrée par le générateur
Enregistrer dans h:\travail\ts2 le fichier au format txt ( enregistrer sous/ format de fichier : texte (
votrenom.txt / ajouter T et Uc )
Laisser le fichier ouvert dans Synchronie et ne pas fermer synchronie !
4- Evolution de Uc au cours du temps
Ouvrir le fichier dans Excel
Tracer Uc = f(t) [ format de série de données : marques aucune ; trait automatique , lissage . Mettre
des graduations secondaires aux axes.
TS
Charge et décharge d’un
condensateur

2
Enregistrer sous un nom à l’extension .xls (sinon le graphe sera perdu )
Imprimer uniquement le graphe ( après l’avoir sélectionné).
Modélisation
Rajouter une colonne Uc mod
La solution de l’équation différentielle décrivant le comportement de la charge du
condensateur est :
Uc =E(1 – e – t/)
Ecrire la valeur de R×C ) dans une cellule quelconque sur la 1ère ligne.
Entrer la formule suivante dans la colonne Uc mod : = ¯*(1-exp(-U/B) où : ¯:valeur de la tension E
mesurée ; U: cellule ou se trouve l’instant t correspondant ; Badresse de la cellule où l’on a écrit ,
rajouter ensuite $ devant l’adresse de la cellule ( lettre et chiffre) pour la rendre absolue (ou appuyer
sur F4).
Recopier vers le bas
Copier la colonne et coller sur le graphe. Mettre en forme pour obtenir une courbe continue. Si les deux
courbes ne correspondent pas faire varier la valeur de 
5- Evolution de l’intensité pendant la charge
L’intensité du courant pendant la charge est donné par i = E – Uc
R
Retour vers synchronie :
traitements/feuille de calcul :
Ecrire i = (N-Uc)/ ?
Avec N: valeur de E et ?: valeur de R.
Paramètres/courbes : i , cocher fenêtre 2.
Paramètres/ fenêtres/fenêtre2 /echelle en y : basée sur i
Observer ensuite l’évolution de i en fonction du temps.
Enregistrer sous format .txt en important uniquement T et i
Modélisation On montre que i = E
Re-t/
Ouvrir le fichier txt dans Excel
Rajouter une colonne imod dans laquelle on entre la formule donnant i
Tracer i et imod = f(t) sur un même graphe. Imprimer ce graphe.
Exploitation
A Charge d’un condensateur à courant constant
Graphes :
Tracer Uc = f(t) pour chacun des deux condensateurs sur un même graphe. Trouver l’équation de
chaque droite
Dans le cas du premier condensateur, rajouter une colonne pour calculer q (charge à l’instant t) et
compléter cette colonne sachant que q ( C ) = I(A)×t (s). Tracer ensuite q = f(Uc). Trouver l’équation de
la droite
Interprétation
1. Sachant que q = I×t et connaissant l’équation de U = f(t) Montrer en éliminant t dans les deux
équations que l’on peut exprimer q en fonction de U et ainsi montrer que q ( C) = C (F)×U(V).
Vérifier avec les valeurs des capacités des condensateurs choisis.
2. Vérification : Que représente le coefficient directeur de la droite du graphe q = f(U)
B Echelon de tension
1. Constante de temps 
Sur le graphe Uc = f(t) , faire la construction graphique nécessaire pour déterminer .
Comparer cette valeur avec calculé et donner la précision de la mesure.
2. équation différentielle
Montrer qu’au bout d’un temps la valeur de Uc est de 63% de celle de E
3. intensité
Montrer que i = E – Uc
R
Trouver par un raisonnement la valeur de i0 ( à t=0) .
Vérifier la valeur de i0 sur le graphe
Sur le graphe, à partir de quel instant la valeur de i s’annulle t-elle ? Pourquoi ?
4. Montage
On aurait pu réaliser une acquisition de i avec Synchronie. Un tel logiciel, comme un oscilloscope, ne
peut mesurer que des tensions. On ne peut donc qu’utiliser la loi d’Ohm pour mesurer i.
Dessiner le montage que l’on aurait du faire pour voir l’évolution de i sur l’écran de
l’ordinateur.