Contribution `a l`analyse des premi`eres données de l

Facult´ e des Sciences appliqu´ ees MA2 - Physique
Contribution ` a l’analyse des
premi` eres donn´ ees de l’exp´ erience
CMS au LHC.
Promoteurs : Sparenberg Jean-Marc et Vanlaer Pascal
Alaluf David
M´emoire de fin d’´etudes pr´esent´e en vue de l’obtention
du titre d’ing´enieur civil physicien
Universit´ e Libre de Bruxelles
Ann´ ee acad´ emique 2009-2010

Table des mati`eres
0 Introduction 4
1 Particules ´el´ementaires et leurs interactions 6
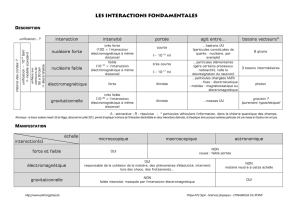
1.1 Les interactions fondamentales . . . . . . . . . . . . . . . . . . 6
1.2 Lesleptons ............................ 8
1.3 Lesquarks............................. 9
1.4 Structure des hadrons . . . . . . . . . . . . . . . . . . . . . . 9
2 Pr´esentation du projet LHC 13
2.1 Led´etecteurCMS......................... 14
2.1.1 D´etecteur de traces . . . . . . . . . . . . . . . . . . . . 18
2.1.2 Calorim`etre ´electromagn´etique . . . . . . . . . . . . . . 22
2.1.3 Calorim`etre hadronique . . . . . . . . . . . . . . . . . 24
2.1.4 Chambres `a muons . . . . . . . . . . . . . . . . . . . . 24
3 Physique des collisions proton-proton au LHC 26
3.1 Le processus de Drell-Yan . . . . . . . . . . . . . . . . . . . . 26
3.1.1 Motivation......................... 26
3.1.2 Aper¸cu th´eorique . . . . . . . . . . . . . . . . . . . . . 27
3.1.3 Bruitdefond ....................... 28
3.2 Section efficace d’un processus . . . . . . . . . . . . . . . . . . 30
3.2.1 Section efficace partonique . . . . . . . . . . . . . . . . 30
3.2.2 Section efficace hadronique . . . . . . . . . . . . . . . 31
3.2.3 Les fonctions de distribution de partons . . . . . . . . 32
3.3 Corrections d’ordre sup´erieur . . . . . . . . . . . . . . . . . . 34
3.4 Analyse cin´ematique du processus de Drell-Yan . . . . . . . . 35
3.4.1 Distributions cin´ematiques . . . . . . . . . . . . . . . . 36
√s=900GeV ...................... 36
√s=7TeV........................ 44
3.4.2 Section efficace et acceptance . . . . . . . . . . . . . . 48
1

TABLE DES MATI ` ERES TABLE DES MATI ` ERES
4´ Etude de la production de particules ´etranges `a 900 GeV 50
4.1 Reconstruction et s´election des ´ev`enements . . . . . . . . . . . 52
4.1.1 Reconstruction de la trace . . . . . . . . . . . . . . . . 52
4.1.2 S´election des ´ev`enements . . . . . . . . . . . . . . . . . 53
4.1.3 Reconstruction des V0.................. 53
4.1.4 Identification des V0................... 54
4.2 Simulations Monte Carlo et donn´ees du CERN . . . . . . . . . 61
4.2.1 S´election des V0...................... 61
4.2.2 Distributions cin´ematiques des V0............ 65
4.3 Tempsdevie ........................... 68
4.3.1 M´ethode.......................... 70
4.3.2 Correction `a une dimension . . . . . . . . . . . . . . . 71
4.3.3 Correction `a deux dimensions . . . . . . . . . . . . . . 74
Conclusion 76
2

Remerciements
Je tiens `a remercier les diff´erentes personnes qui m’ont soutenu de pr`es
ou de loin pour la r´ealisation de ce projet de fin d’´etudes.
En effet, d`es le premier jour j’ai ´et´e chaleureusement accueilli et int´egr´e par
toute l’´equipe. J’aimerais remercier Barbara Clerbaux, Pierre Marage, Jean-
Marc Sparenberg, Anne-Sophie Kalbfleisch, Vincent Dero, Laurent Favart et
Otman Charaf pour l’aide et les pr´ecieux conseils qu’ils m’ont apport´es, ainsi
que Laurent Thomas pour toutes les nuits que nous avons pass´ees ensemble
au labo (`a travailler) !
Je remercie tout particuli`erement Mr. Pascal Vanlaer pour l’attention et le
temps qu’il m’a accord´es tout au long de mon travail.
Grˆace `a vous tous, cette exp´erience m’a ´et´e tr`es enrichissante `a tous les
niveaux.
3

R´esum´e
Dans ce travail, nous avons dans un premier temps ´etudi´e la cin´ematique de
production du Boson Z se d´esint´egrant dans le canal di-´electronique lors du
processus de Drell-Yan. Cette ´etude a ´et´e men´ee `a des ´energies de 900 GeV,
7 TeV et 10 TeV dans le centre de masse de la collision proton-proton. Les
donn´ees analys´ees ont ´et´e fournies par le programme de simulation Monte
Carlo, PYTHIA. Les distributions cin´ematiques obtenues nous ont permis
de comprendre l’´evolution de l’acceptance du d´etecteur ainsi que la section
efficace du processus de Drell-Yan.
Dans un second temps, nous nous sommes int´eress´es `a la production de par-
ticules neutres ´etranges, les V0, lors de l’´ev`enement sous-jacent du proces-
sus de Drell-Yan. Nous avons analys´e les distributions cin´ematiques de ces
particules ´etranges, sur base de simulations de reconstruction de particules
g´en´er´ees par Monte Carlo et de coupures faites sur les masses invariantes
pour tenter d’identifier ces V0. Nous avons ´egalement compar´e ces r´esultats
aux toutes premi`eres donn´ees `a 900 GeV, r´ecolt´ees en 2009 dans l’exp´erience
CMS au LHC. Par apr`es, nous avons ´etudi´e l’efficacit´e de reconstruction des
produits de d´esint´egration de ces particules ´etranges. Nous avons finalement
pr´esent´e une m´ethode de reconstruction du temps de vie des V0et compar´e
les r´esultats obtenus `a la moyenne mondiale. Nous avons termin´e ce travail
en proposant l’´etude de certains aspects encore mal compris.