19- Courants dérivés

22 courants dérivés
Plan détaillé
A – répartition des
courants
1 1 – conducteurs en série
a – Montage
b – Intensité
c – Tension
d – Résistance équivalente
2 2 – conducteurs en dérivation ou en parallèle
a – Montage
b – Intensité
c – Tension
d – Résistance équivalente
1o- Définition et mesure
2o- Théorème des conductances
3o- Calcul des intensités des courants dérivés
B – applications
1 – shunt des ampèremètres
Un shunt est une faible résistance, que
l’on monte entre les bornes d’un
ampèremètre afin de dériver la plus
grande partie du courant en dehors de
l’appareil, ce qui permet de l’utiliser pour
mesurer des courants d’intensité
supérieure à son calibre.
2 – montage des lampes

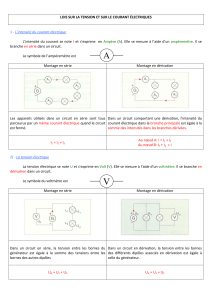
1 – conducteurs en série
a - Montage
Entre deux points d’un circuit électrique, montons plusieurs conducteurs :
deux résistances R1 et R3, une lampe R2 et un ampèremètre. Puisque ces
conducteurs sont placés bout à bout, on dit qu’ils sont montés en série.
b – Intensité
Faisons passer un courant électrique dans ces conducteurs : l’ampèremètre
indique une intensité I.
Coupons chaque conducteur et intercalons un ampèremètre dans chaque
coupure. Faisons passer le courant, les ampèremètres indiquent tous la
même intensité I.
Donc : Quand des conducteurs sont montés en série, l’intensité du
courant qui les traverse est la même pour tous.
c – Tension
Conservons le montage précédent et mesurons la d.d.p. entre les extrémités
A et D de la série, nous lisons la valeur U.
Mesurons successivement la d.d.p. entre les extrémités de chaque portion de
la série; nous lisons successivement les d.d.p. U1, U2, U3, et nous constatons
que : U = U1 + U2 + U3.
Donc : Quand des conducteurs sont montés en série, la tension entre les
extrémités de la série est égale à la somme des tensions entre les
extrémités de chaque portion de la série.
CONCLUSION ► Dans un montage en série :
─ l’intensité est la même dans toutes les parties du circuit,
─ les tensions aux bornes des différentes portions s’ajoutent.
d – Résistance équivalente
Les résistances r1, r2, r3, montées
entre les points A et D du circuit,
sont traversées par le même
courant d’intensité I.

La loi d’Ohm s’écrit, pour chacune d’elles :
VA  VB = r1 ٠ I
VB  VC = r2 ٠ I
VC  VD = r3 ٠ I
soit , en additionnant membre à membre :
VA  VD = I (r1 + r2 + r3).
L’ensemble des conducteurs r1, r2, r3, est équivalent à un conducteur unique
de résistance :
Lorsque plusieurs conducteurs sont placés en série leurs résistances
s’ajoutent.
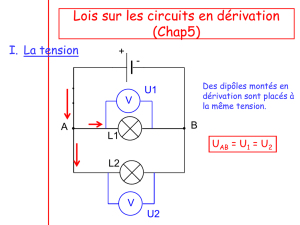
2 – conducteurs en dérivation
a – Montage
Soit un circuit électrique
comprenant, entre deux points
A et B, deux (ou plusieurs)
branches allant toutes de A en
B. On dit que ces branches
sont montées en dérivation ou
en parallèle.
On appelle :
─ courant principal, le courant I qui circule avant et après les dérivations;
─ courants dérivés, les courants qui circulent dans les branches en dérivation.
b – Intensité
Intercalons un ampèremètre dans le circuit principal : il indique une intensité I.
Intercalons successivement un ampèremètre dans chacune des dérivation :
nous lisons respectivement des intensités i1, i2, et nous constatons que :
I = i1 + i2.
Donc : Quand des conducteurs sont montés en dérivation, l’intensité du
courant principal est égale à la somme des intensités des courants
dérivés.
c - Tension
Avec un voltmètre, mesurons la d.d.p. entre les points A et B du circuit
précédent : nous lisons une tension U.
Mesurons successivement la tension entre les points A1 et B1 de la première
dérivation, A2 et B2 de la seconde dérivation, tous ces points étant
respectivement très proches de A et B : nous lisons toujours la même tension
U.
Donc : Quand des conducteurs sont montés en dérivation, la différence
de potentiel entre les extrémités de chaque branche est la même.
R = r1 + r2 + r3

CONCLUSION ► Lois des courants dérivés.
Dans un montage en dérivation :
─ l’intensité du courant principal est égale à la somme des intensités
des courants dérivés,
─ les tensions aux bornes des dérivations sont égales.
Il résulte de tout ce qui précède que;
─ Dans un montage en série, tous les appareils sont traversés par la même
intensité.
─ Dans un montage en dérivation, tous les appareils sont soumis à la même
différence de potentiel.
d – Résistance équivalente
1o – Définition et mesure. On nomme
résistance équivalente à l’ensemble des
dérivations r1, r2, et r3 la résistance unique R
qui, placée entre les points M et N, maintient
entre ces points la même d.d.p. que
l’ensemble des dérivations en laissant
passer un courant de même intensité dans
le circuit principal.
Soit R la résistance équivalente à
l’ensemble des 3 résistances r1, r2 et r3 de la
figure ci-contre. R doit être telle que l’on ait, d’après la loi d’Ohm :
 .
D’autre part, appliquons la loi d’Ohm à chaque dérivation :
U = r1i1. D’où: i1 =
 .
U = r2i2. D’où: i2 = 
 .
U = r3i3. D’où: i3 = 
 .
Or: I = i1 + i2 + i3.
Ou: 
 + 
Simplifions par U :
L’inverse de la résistance équivalente est égale à la somme des inverses des
résistances montées en parallèle.

2o – Le théorème des conductances. On appelle conductance d’un
conducteur l’inverse 1/R de sa résistance ; le résultat précédent exprime le
théorème des conductances :
La conductance d’un ensemble de conducteurs placés en dérivation est
égale à la somme des conductances de ceux-ci.
Remarque.─ 1. Le rapport 1/R est plus grand que tout rapport 1/r ; donc
R < r.
2. Si l’on monte n résistances égales à r, la formule ci-dessus devient :
1/R = 1/r + 1/r + 1/r + …+ 1/r = n fois 1/r = n/r.
On en déduit : R =
 .
3o – Le calcul des intensités des courants dérivés. Connaissant l’intensité
I du courant principal et les résistances r1, r2, r3, des dérivations, le calcul de
la résistance équivalente conduit à la détermination des intensités i1, i2, i3.
Par définition, on doit donc avoir :
RI = U = r1i1 = r2i2 = r3i3 = …,
on en déduit : i1 = 
 , i2 =   , i3 =   .
Exercices types
1 – Trois résistances mortes, r1=2Ω, r2=3Ω, r3=6Ω,
sont montées en dérivation entre deux points M et N
présentant une d.d.p. de 12V.
1o – Calculer les intensités des courants circulant
dans chacune de ces résistances.
2o – En déduire l’intensité du courant dans le circuit
principal et la valeur de la résistance équivalente, R.
3o – Vérifier ce dernier résultat en calculant R à partir
de r1, r2, r3 (directement).
Solution
1o – Les intensités des courants circulant dans chacune des branches sont
données par l’application de la loi d’Ohm :
2o – L’intensité du courant dans le circuit principal est la somme des intensités
des courants dérivés :