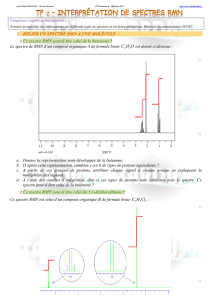
Etude de la statistique spatio-temporelle des

ε
α β

2,5.10−5m25mm ×5mm
25◦C
~n
~ex~ez
~ey(~ex, ~ey, ~ez)
(O, ~ex, ~ey)
InSn2O3

θ ~n (O, ~ex, ~ey)φ
~n (~ex, ~ey)~ex~n (~ex, ~ey, ~ez)
nx= cos θ. cos φ ny= cos θ. sin φ nz=sinθ ~n θ φ ~r
V
Vc
θ(z)
θ=θmsin(πz
L)
0 0.5 1 1.5 2 2.5 3 3.5
0
0.5
1
1.5
θm
V/Vc
~
E
θmz=L
2
θmV
Vc
ε=³V
Vc´2−1
θ(~r) = θ0(z) + δθ(~r)

~ex
neno
λ
ϕ
ϕ=2π
λZL
0
neff [θ(z)] −nodz nef f [θ(z)] = neno
qn2
ocos2θ(z) + n2 esin2θ(z)
θ
θ0(z)
ϕ0θ θ =θ0+δθ
ϕ=ϕ0+δϕ
αPαA
~ex
~uP~uAαPαA~ex
ϕ=ϕ0+δϕ
~
ki(~ Ei,~ Bi)
(~ Et,~ Bt)ϕ
αP
ϕ
ϕ0
I0
ϕ
I=I0[cos2(αP−αA)−sin(2αP) sin(2αA) sin2(ϕ
2)]
ϕ