TS-P06 Cours - Physique

TS www.pichegru.net 29 mars 2017
-1-
P6 : Mécanique quantique
Plan du chapitre
Présentation historique
Transferts quantiques d’énergie
Rappels de 1
ère
S
Rayonnement EM et types de transition
Dualité onde-particule
Quantité de mouvement et longueur d’onde associée
Onde de matière
Encore plus étrange
Aspect probabiliste de la mécanique quantique
Les lasers
Émission stimulée
Éléments du laser
Caractéristiques de la lumière émise
P Pr ré és se en nt ta at ti io on n h hi is st to or ri iq qu ue e
Petite histoire de la mécanique quantique
T
T
Tr
r
ra
a
an
n
ns
s
sf
f
fe
e
er
r
rt
t
ts
s
s q
q
qu
u
ua
a
an
n
nt
t
ti
i
iq
q
qu
u
ue
e
es
s
s d
d
d’
’
’é
é
én
n
ne
e
er
r
rg
g
gi
i
ie
e
e
Associer un domaine spectral à la nature de la transition mise en jeu.
L’énergie d’une entité microscopique (atomes, ions, molécules, noyaux,
électrons, etc.) ne peut pas prendre n’importe quelle valeur. Elle est
quantifié.
R Ra ap pp pe el ls s d de e 1 1
è
èr re e
S S
Quantification d’énergie de l’électron
L’électron d’un atome ne peut absorber un photon uniquement si l’énergie
de celui-ci correspond exactement à la différence entre deux niveaux
d’énergie possible de l’électron. Il passe alors d’un niveau d’énergie bas à
un niveau d’énergie plus élevé.
De même, lors de sa désexcitation (passage d’un niveau d’énergie vers un
niveau d’énergie moindre), l’électron émet un photon dont l’énergie
correspond exactement à la différence d’énergie entre les deux niveaux.
Photon et fréquence du rayonnement EM
L’énergie d’un photon associé à un rayonnement de fréquence ν est :
E = h · ν
h est la constante de Planck : 6,63·10
-34
m
2
·kg·s
-1
R Ra ay yo on nn ne em me en nt t E EM M e et t t ty yp pe es s d de e t tr ra an ns si it ti io on n
Transition entre deux états d’énergie électroniques : rayonnement UV ou
visible (ou rayons X pour les e
–
« de cœur », proche du noyau)
Transition entre deux états d’énergie vibrationnel (oscillation des
liaisons) : rayonnement IR.
Transition entre deux états énergétiques du noyau : rayonnement γ
D
D
Du
u
ua
a
al
l
li
i
it
t
té
é
é o
o
on
n
nd
d
de
e
e-
-
-p
p
pa
a
ar
r
rt
t
ti
i
ic
c
cu
u
ul
l
le
e
e
Extraire et exploiter des informations sur les ondes de matière et sur la
dualité onde-particule.
Savoir que la lumière présente des aspects ondulatoire et particulaire
Connaître la relation p = h/ λ
Identifier des situations physiques où le caractère ondulatoire de la
matière est significatif.
Toutes les particules, massives (électron, nucléon, muons) ou non
(photons, neutrino ?) possèdent à la fois des propriétés corpusculaires et
des propriétés ondulatoires.
Q Qu ua an nt ti it té é d de e m mo ou uv ve em me en nt t e et t l lo on ng gu ue eu ur r d d’ ’o on nd de e
a
as ss so oc ci ié ée e
Toutes les particules possèdent une quantité de mouvement :
• p = mv (matière non-relativiste)
• p = E/c (photon)
• p = h / λ (pour les 2)
O On nd de e d de e m ma at ti iè èr re e
Les ondes de matière associées aux particules microscopiques présentent
les mêmes phénomènes ondulatoires (interférence, diffraction, etc) que les
ondes électromagnétique.
Une onde de matière pour interférer ou diffracte si elle rencontre un
obstacle de taille a tel que a ~ λ . Dans certaines conditions, des e
–
peuvent
interférer entre eux !!
E En nc co or re e p pl lu us s é ét tr ra an ng ge e
Il est possible de faire interférer des photons ou des électrons lorsqu’on les
fait passer par une double fente, même s’ils passent un à un !!!
Plus fou encore : si, grâce à ses appareils de mesure, on cherche à savoir
par laquelle des deux fentes est passé l’électron, celui-ci recommence à se
comporter comme une particule et le motif d’interférence disparaît !
L’observation d’une particule a des effets sur son comportement !
Dr Quantum and the double slit experiment
A
A
As
s
sp
p
pe
e
ec
c
ct
t
t p
p
pr
r
ro
o
ob
b
ba
a
ab
b
bi
i
il
l
li
i
is
s
st
t
te
e
e d
d
de
e
e l
l
la
a
a m
m
mé
é
éc
c
ca
a
an
n
ni
i
iq
q
qu
u
ue
e
e
q
q
qu
u
ua
a
an
n
nt
t
ti
i
iq
q
qu
u
ue
e
e
Extraire et exploiter des informations sur les phénomènes quantiques
pour mettre en évidence leur aspect probabiliste.
En mécanique quantique, pas de déterminisme, mais une probabilité
d’avoir certains comportements.
Par exemple : On ne sait pas quand un atome va se désexciter, seulement
la probabilité qu’il a de se désexciter pendant une durée donnée. Idem pour
la désexcitation d’un noyau radioactif.
Einstein refusait cela et aurait dit : « Dieu ne joue pas aux dés ». Ironie de
l’histoire, car c’est lui qui a posé une des pierres angulaires de la physique
quantique...
 Bonus :
Le principe d’Heisenberg expliqué simplement.
What is the Uncertainty Principle?

TS www.pichegru.net 29 mars 2017
-2-
L
L
Le
e
es
s
s l
l
la
a
as
s
se
e
er
r
rs
s
s
Connaître le principe de l’émission stimulée et les principales
propriétés du laser (directivité, monochromaticité, concentration spatiale
et temporelle de l’énergie).
É Ém mi is ss si io on n s st ti im mu ul lé ée e
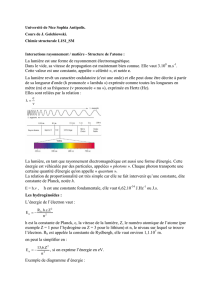
Émission d’un photon par une entité excitée (= pas à son énergie
fondamentale ou minimale) provoquée par un photon de même énergie que
celui émis. Le photon émis est « jumeau » de celui qui a provoqué la
désexcitation.
É Él lé ém me en nt ts s d du u l la as se er r
• Milieu actif (ou amplificateur) : où se produit l’émission stimulée par les
entités excités. Pour les lasers du lycée, il s’agit d’un mélange He-Ne.
• Dispositif de pompage : donne l’énergie nécessaire au milieu actif pour
faire passer les entités émettrices dans un état excité.
• Cavité résonnante : disposant d’un miroir à chaque extrémité pour créer
des allers-retours de photons afin d’entretenir les émissions stimulées.
C Ca ar ra ac ct té ér ri is st ti iq qu ue es s d de e l la a l lu um mi iè èr re e é ém mi is se e
Cette lumière est dite « cohérente » à cause des caractéristiques suivantes :
• Monochromaticité : tous les photons ont la même énergie.
• Cohérence spatiale : tous les photons vont dans la même direction, le
faisceau est donc très concentré.
• Cohérence temporelle : toutes les vibrations associées à chaque photon
sont en phase.
De plus, l’impulsion lumineuse peut être rendue extrêmement brève
(concentration dans le temps).
Toutes ces caractéristiques font que le rayonnement laser assure une
grande concentration de l’énergie lumineuse, dans l’espace (directivité),
dans le spectre (monochromaticité) et dans le temps (impulsion).
C’est pas sorcier : les lasers
Énergie de l’atome
Photon
∆E = h ν Photon jumeau
∆E = h ν
E
haut
E
bas
dispositif de pompage
qui fournit de l’énergie
milieu amplificateur
miroir miroir semi-réflechissant
faisceau laser