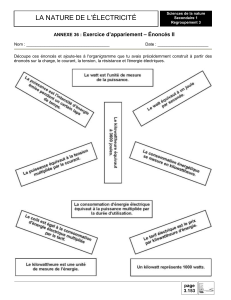
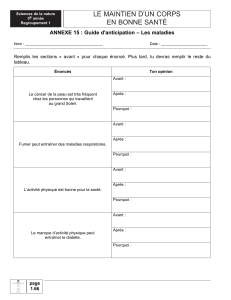
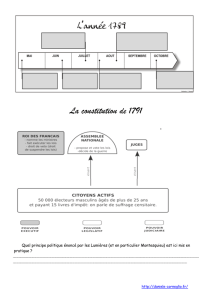
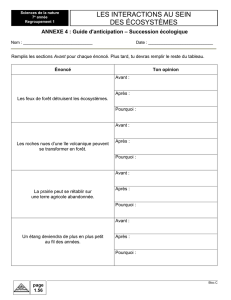
Notions de Logique

Notions de Logique
Marcel Crabbé

Première partie
Correspondance et démonstration

1 Introduction
1 La notion de loi logique
En première approximation, une loi logique est une vérité nécessaire et, partant,
absolument générale. Examinons les cinq phrases vraies 1suivantes, rangées par ordre
croissant de généralité :
(1) Il pleut
(2) Descartes est mort le 11 février 1650
(3) Tous les corbeaux sont noirs
(4) 1+16= 0
(5) La neige est blanche ou n’est pas blanche
(1) est vraie ici et maintenant en raison de la note 1. Mais elle ne l’est pas ailleurs,
elle ne l’a pas toujours été ici, ni ne le sera probablement pas toujours.
La phrase (2), en revanche, est partout vraie et elle le restera toujours. On peut
même soutenir qu’elle l’a toujours été. Cette phrase est, en ce sens, plus générale
que la première, car elle se réfère à un état de fait qui ne peut être changé que si
l’on envisage une situation ou un monde différent du monde usuel. Toutefois, il est
facilement concevable que la mort de Descartes ait eu lieu le 10 février 1650 ou le
12 février 1650. Dans ces deux cas, la phrase (2) n’est pas vraie.
(3) énonce une loi empirique. Comme les deux phrases précédentes elle est vraie,
mais on ne peut lui enlever cette qualité aussi aisément. Pour cela, il faudrait, par
exemple, se placer dans un monde où certains corbeaux sont blancs ou vert pomme.
Dans la mesure où un tel monde doit être sensiblement plus étrange que celui dans
lequel nous vivons ou que certaines des situations ou mondes qui rendent la phrase
(2) non vraie, la phrase (3) est considérée comme étant davantage nécessaire que la
phrase (2).
Dans le cas de la phrase (4), il semble tout à fait impossible qu’il y ait un monde
dans lequel elle puisse ne pas être vraie. Cela vient de ce que le sens des symboles
1. À lire par temps pluvieux.

Logique 4
1,+,6=et 0est tel que cette phrase décrit un état de fait indépendant de toute
expérience. Supposons cependant que l’on modifie l’interprétation donnée à ces
symboles, en interprétant +, par exemple, par l’opération de soustraction. Alors (4)
n’est pas vraie. Il en va de même si l’on convient que le symbole 1désigne le nombre
0ou si on calcule modulo 2. Ici, nous avons affaire à une vérité mathématique : il
est impossible de ne pas la supposer vraie sans changer le sens des symboles utilisés.
De même, on voit que, si on modifie l’interprétation usuelle du mot ‘Descartes’, le
sens du mot ‘mort’, le calendrier ou encore le sens de ‘corbeaux’ ou de ‘noirs’, on
peut facilement enlever leur vérité aux phrases (2) et (3).
Aucune des quatre phrases, examinées jusqu’ici, n’est donc invariante, quant à
sa vérité, relativement aux situations différentes de la nôtre ou aux interprétations
non courantes.
Par contre, la phrase (5) demeure invariablement vraie, quel que soit le monde
envisagé et quelle que soit l’interprétation que l’on donne dans ce monde aux mots
‘neige’, ou ‘blanche’. En d’autres termes, elle est logiquement vraie. Il en est de
même pour des phrases comme ‘Il n’est pas vrai que la neige est noire et n’est pas
noire’ ou ‘S’il pleut, alors il pleut’.
Une première définition de la notion de loi logique peut donc être avancée :
Une loi logique est une phrase qui est vraie dans tous les mondes
possibles quelle que soit la manière dont on l’interprète.
Cette définition peut être complètement explicitée 2. Il suffit pour cela de préciser
d’abord ce qu’il convient d’entendre par « phrase » (ou « énoncé »), d’introduire
ensuite un concept de « modèle », qui rendra précises les notions de monde possible
et d’interprétation dans un monde possible et enfin, d’expliquer ce qu’on entend
par :
l’énoncé Aest vrai dans le modèle M,
ou plus brièvement :
Mest modèle de A,
ce qui se note :
M |=A
La définition précédente peut alors être formulée comme suit :
Une loi logique est un énoncé qui est vrai dans tous les modèles.
Notons
|=A
2. Cela a été fait par les logiciens contemporains, principalement par Tarski.

Logique 5
l’expression ‘A est une loi logique’. On a donc :
|=Assi M |=A, pour tout modèle M.
B1. Quand on fait varier l’interprétation d’une phrase, on ne fait pas varier
l’interprétation de toutes ses composantes. Des expressions comme ‘est’, ‘ou’, ‘il
n’est pas vrai que’, ‘tous’, ‘et’, etc. s’interprètent toujours de la même manière
dans tous les mondes possibles. Pour cette raison, on les considère comme
des expressions logiques. D’autre part, des expressions qui, comme ‘neige’,
‘corbeau’, ‘noir’, etc. peuvent recevoir diverses interprétations, dans ce monde-ci
ou dans d’autres mondes, sont des expressions réputées non logiques.
2. L’interprétation des éléments non logiques d’une phrase ne peut cependant
être totalement arbitraire. On peut sans doute interpréter ‘la neige’ par « So-
crate » et ‘noir’ par le concept « grec », mais l’inverse n’est pas admis. Les règles
d’interprétation étant assez compliquées, bornons-nous à signaler qu’une inter-
prétation doit seulement respecter la structure, les catégories et les fonctions
grammaticales dans les grandes lignes. En particulier, l’interprétation d’un syn-
tagme nominal, comme un nom propre, doit être un objet ou un individu et
l’interprétation d’un syntagme verbal doit être une propriété.
3. Si on fixe, une fois pour toutes, le sens de certains mots, comme on l’a fait
ci-dessus, alors il y a des énoncés qui sont toujours vrais et d’autres qui parfois
ne le sont pas. En distinguant ainsi deux sortes de mots, les mots logiques et
les mots non logiques, ceux qui recevront une même interprétation dans tout
modèle et ceux dont l’interprétation sera variable, on distingue également deux
types d’énoncés.
Si on définit un connecteur logique comme étant une expression qui est
interprétée de la même façon dans tout modèle, on définit également un
modèle comme un monde dans lequel une expression logique reçoit un sens
dit « standard ». L’extension de la notion de modèle varie donc avec celle de la
notion de mot logique.
Plus généralement, supposons qu’en fixant le sens d’un mot, on le promeuve au
rang de constante logique. En ce cas, on ne considérera comme modèle que ceux
qui satisfont à cette définition. Par exemple, si on décide que ‘homme’ est une
constante logique en assimilant son extension à ce qui est vérifié par ‘animal’
et par ‘raisonnable’, alors ‘Tout homme est animal’ devient une loi logique, à
condition bien sûr que ‘tout’ et ‘est’ aient leur rôle usuel de constante logique.
On a ainsi fait ce qu’on pourrait appeler une logique du mot ‘homme’. Celle-ci
peut ensuite être complétée par une logique de ‘animal’ et de ‘raisonnable’. En
général, faire la ou une logique d’un mot, c’est en fixer le sens intégralement
(définition explicite) ou partiellement (définition implicite).