TD 1 Etude d`un réseau optique - Laboratoire de Physique des Lasers

M2 OMP Option Mati`ere Froide Mercredi 6 janvier 2016
TD 1
Etude d’un r´eseau optique
La lumi`ere d’un laser peut ˆetre utilis´ee pour manipuler l’´etat externe des atomes.
En particulier, une paire de faisceaux lasers se propageant en sens oppos´es produit une
onde stationnaire, r´esultant en un potentiel p´eriodique pour les atomes. Ce potentiel 1D
peut ˆetre g´en´eralis´e `a 2D et 3D avec 2 ou 3 paires de faisceaux. On reproduit ainsi une
situation analogue `a celle des ´electrons dans un cristal, o`u le potentiel p´eriodique est form´e
par les ions du cristal. Ce dispositif o`u la lumi`ere remplace le cristal est appel´e un r´eseau
optique. Il est largement utilis´e avec des condensats de Bose-Einstein pour des exp´eriences
de physique atomique o`u les atomes dans le r´eseau optique constituent un syst`eme mod`ele
des ´electrons dans les solides. En m´etrologie, les r´eseaux optiques constituent un ingr´edient
essentiel des horloges optiques `a atomes neutres (voir cours 7). Enfin, une onde stationnaire
puls´ee peut ˆetre utilis´ee dans un interf´erom`etre pour r´ealiser une s´eparatrice ou un miroir
par diffraction (voir cours 4).
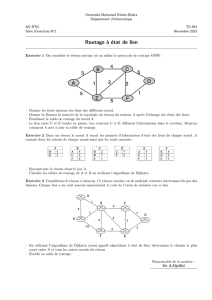
Figure 1 – R´eseau optique 2D (a) et 3D (b). Figure extraite de [1].
1

1 Forces radiatives
On consid`ere un atome `a deux niveaux |giet |eis´epar´es par une ´energie ¯hω0. L’´etat
excit´e |eia une dur´ee de vie finie Γ−1. On note dle dipˆole r´eduit associ´e `a la transition
g→e.
L’atome est plac´e dans une onde laser de fr´equence ω, de polarisation e(r) et de champ
´electrique E(r, t) = E(r)
2(e−iωt e−iφ(r)e(r) + c.c.). On appelle δ=ω−ω0le d´esaccord `a
la r´esonance et Ω(r) = −(d.e)E(r)/¯hla pulsation de Rabi associ´ee `a l’interaction entre
l’atome et le champ.
1. Donner l’expression du param`etre de saturation s(r) en fonction des donn´ees.
2. Rappeler l’expression de la force radiative moyenne qui s’exerce sur un atome au
repos. On mettra en ´evidence deux termes Fpr et Fdip.
3. Que vaut Fpr pour une onde plane de vecteur d’onde ket de saturation s0? Com-
menter.
4. Donner l’expression de la force dipolaire Fdip et du potentiel Udip(r) dont elle d´erive,
en fonction de δet s(r).
5. Dans toute la suite, le d´esaccord est choisi tr`es grand devant la largeur de l’´etat excit´e
(|δ|  Γ) et devant la pulsation de Rabi (|δ|  Ω). Mettez le potentiel dipolaire
sous la forme
Udip(r) = ¯hΩ(r)2
4δ(1)
2 R´eseau optique
L’onde stationnaire qui produit le r´eseau optique r´esulte de l’interf´erence de deux
faisceaux lasers de mˆeme polarisation se propageant en sens oppos´es selon l’axe x. Ces
faisceaux gaussiens ont un rayon tr`es grand devant la taille du nuage atomique, de sorte
qu’on peut les mod´eliser par deux ondes planes.
1. Les deux faisceaux proviennent du mˆeme laser. Quelle condition doit v´erifier la lar-
geur spectrale du laser pour que l’on n’ait pas `a se pr´eoccuper `a mieux que le m`etre
de la longueur relative parcourue par les deux faisceaux avant superposition sur les
atomes ?
2. On suppose que la condition trouv´ee `a la question pr´ec´edente est remplie. Les deux
ondes sont polaris´ees lin´eairement selon l’axe y. Leur champ ´electrique respectif
s’´ecrit :
E±(r, t) = E0
2e−iωt±ikxey+ c.c.(2)
o`u k=ω/c. Donner l’expression du champ ´electrique total produit par les deux
ondes.
3. Donner l’expression de la fr´equence de Rabi Ω(x) du champ total en fonction de la
fr´equence de Rabi Ω1=−dE0/¯hd’une seule onde plane.
4. Donner la valeur correspondante de la saturation s(x). On notera s0le param`etre
de saturation d’une seule onde plane.
5. Montrer que la force de pression de radiation moyenne Fpr est nulle en tout point.
2

6. Que vaut le potentiel dipolaire U(x) ? Mettez-le sous la forme U(x) = U0cos2kx.
Donner l’expression de U0en fonction de Ω1et δ.
7. L’expression de Uest bien celle d’un potentiel p´eriodique (r´eseau `a 1D). Quelle est
sa p´eriode ? Comment g´en´eraliser ce dispositif en dimension sup´erieure `a 1 ?
3 R´egime de Lamb Dicke
Selon la profondeur du r´eseau (la valeur de U0), il peut ou non y avoir de l’effet tunnel
entre les puits de potentiels voisins. C’est d’ailleurs ce qui est `a la base de l’observation
r´ecente de la transition de phase entre condensat de Bose-Einstein superfluide et isolant
de Mott [2]. Dans le cas o`u le confinement est fort, le r´eseau se comporte comme une s´erie
de micro-pi`eges harmoniques ind´ependants. On peut alors faire la spectroscopie d’une
transition entre deux ´etats pi´eg´es en s’affranchissant de l’effet Doppler li´e au mouvement
des atomes. C’est ce qu’on appelle le r´egime de Lamb Dicke [3], qui joue un rˆole essentiel
pour les horloges optiques `a atomes neutres.
1. On suppose que le d´esaccord δest n´egatif. O`u sont situ´es les minima de potentiel ?
On note x0l’un de ces minima.
2. En d´eveloppant le potentiel dipolaire au voisinage de x0, d´eterminer la fr´equence
d’oscillation ωxdans un micro-pi`ege. On l’exprimera en fonction de U0et de l’´energie
de recul du r´eseau Erec =¯h2k2
2Mo`u Mest la masse de l’atome.
3. Que devient ωxsi δ > 0 ?
4. Les ´etats propres d’un micro-pi`ege sont not´es |nxi, d’´energie nx+1
2¯hωx. On sup-
pose que l’´etat excit´e |eiest pi´eg´e de la mˆeme fa¸con 1. Quelles sont les ´energies des
´etats propres |g, nxiet |e, n0
xi? En d´eduire les fr´equences des transitions que l’on
peut observer entre |giet |ei.
5. Le r´egime de Lamb Dicke est atteint si le pi`ege est si confinant que son ´etat fonda-
mental |nx= 0iest localis´e `a mieux que la longueur d’onde de la transition atomique,
proche de la longueur d’onde du r´eseau : ∆x=q¯h
2Mωx1/k.k∆xest appel´e le
param`etre de Lamb Dicke.
Montrer que cela implique que l’´ecart entre niveaux ¯hωxest grand devant l’´energie
de recul Erec.
6. A quelle condition le r´egime de Lamb Dicke est-il atteint dans le r´eseau ? Commenter
l’approximation harmonique faite plus haut.
7. Montrer que dans ces conditions, le recul lors d’une absorption/´emission est n´egli-
geable devant la largeur de la distribution en impulsion d’un atome pi´eg´e, mˆeme
dans l’´etat fondamental. En cons´equence, la probabilit´e pour un atome de changer
de niveau nxlors d’une ´emission spontan´ee est tr`es faible (de l’ordre de k2∆x2).
8. En quoi le r´egime de Lamb Dicke peut-il ˆetre int´eressant en m´etrologie des fr´equences ?
1. Cela est possible lorsque l’on tient compte de l’ensemble des niveaux atomiques, l’´etat excit´e ´etant
d´eplac´e par interaction avec des ´etats situ´es plus haut en ´energie. Cela se produit pour ceratins atoms `a
une fr´equence appel´ee fr´equence magique . Si l’on r´ealise le pi`ege `a cette fr´equence, la transiont entre g
et en’est pas d´eplac´ee par la lumi`ere. Cette id´ee de Katori [4] a constitu´e le point de d´epart des horloges
optiques `a atomes neutres [5].
3

9. On illumine une assembl´ee d’atomes pi´eg´es dans le r´eseau dans le r´egime de Lamb
Dicke avec un laser proche de la r´esonance atomique. On observe le spectre repr´esent´e
sur la figure 2. Justifier l’allure du spectre observ´e. Que vaut la fr´equence d’oscillation
dans le pi`ege ωxdans cet exemple ? Pour cette s´erie de donn´ees, T= 3 µK et
|U0|= 940 Erec. On donne pour le strontium 87 : Erec/h = 3.46 kHz. Commenter.
Figure 2 – Spectre de r´esonance pour des atomes de strontium 87 confin´es dans un r´eseau
optique. Profondeur du r´eseau |U0|= 940 Erec. Figure extraite de [5].
10. Quelle serait l’allure du spectre si les atomes occupaient uniquement l’´etat fonda-
mental des micro-puits ?
R´ef´erences
[1] Immanuel Bloch, Ultracold quantum gases in optical lattices, Nature Physics 1, 23
(2005).
[2] M. Greiner, O. Mandel, T. Esslinger, T.W. H¨ansch, and I. Bloch, Quantum Phase
Transition from a Superfluid to a Mott Insulator in a Gas of Ultracold Atoms, Nature
415, 39 (2002).
[3] Claude Cohen-Tannoudji, Cours au Coll`ege de France, ann´ee scolaire 1985-1986.
http://www.phys.ens.fr/cours/college-de-france/
[4] H. Katori, M. Takamoto, V.G. Pal’chikov, and V. D. Ovsiannikov, Ultrastable Optical
Clock with Neutral Atoms in an Engineered Light Shift Trap, Phys. Rev. Lett. 91,
173005 (2003).
[5] Pierre Lemonde, Optical lattice clocks, Eur. Phys. Jour. Special Topics 172, 81 (2009).
4