DS4 - Le site de physique de la PCSI

Durée de l’épreuve : 3h00
L’usage de la calculatrice est autorisé
L’énoncé de ce devoir comporte 4 pages
➢ Le barème tiendra compte des commentaires physiques ainsi que des qualités de rédaction.
➢La numérotation des exercices doit être respectée. Les résultats doivent être systématiquement encadrés.
Problème 1 : Microscope optique et microscope électronique
Je vous propose dans ce premier problème de comparer deux microscopes : le microscope optique et le microscope
électronique dont le principe de fonctionnement de ce dernier s'appuie sur l'aspect ondulatoire de la matière.
1. Étude géométrique du microscope optique
Un microscope optique porte les indications suivantes : sur son objectif : * 40 et sur l’oculaire : * 10.
La notice du constructeur précise également :
✔l'ouverture numérique de l’objectif ω = 0,65
✔l'intervalle optique Δ = 16 cm
Le microscope est modélisé par deux lentilles minces convergentes : un objectif L1 de diamètre d = 7,0 mm et un oculaire L2.
Il est réglé pour donner une image à l’infini d’un objet réel AB, perpendiculaire à l’axe optique, A étant placé sur l’axe,
légèrement en avant du foyer principal objet de l’objectif.
Cette image est observée par un œil emmétrope placé au voisinage du foyer image de l’oculaire.
On rappelle que l’ œil emmétrope voit nettement des objets situés entre la distance minimale de vision distincte δ = 25 cm et
l’infini.
1.1. Déterminer le principe de fonctionnement du microscope.
1.2. Faire un schéma du dispositif (sans respecter l’échelle) et tracer soigneusement la marche de 2 rayons lumineux issus du
point B de l’objet AB, l’un émis parallèlement à l’axe optique, l’autre passant par le foyer principal objet F1 de l’objectif de
centre optique O1.
1.3. L’indication portée sur l’oculaire (*10) est le grossissement de l'oculaire, c’est-à-dire le rapport de l’angle sous lequel
on voit l’image intermédiaire à travers l’oculaire et l’angle sous lequel on voit cette même image intermédiaire à l’œil nu
lorsqu’elle est située à la distance minimale de vision distincte δ = 25 cm. On pourra poser G2 = 10.
Déterminer la distance focale image f'2 de l’oculaire.
1.4. L’intervalle optique Δ correspond à la grandeur algébrique
F '1F2
.
La valeur absolue du grandissement de l’objet AB par l’objectif sera noté γ1 = 40, il s'agit de l'indication *40.
Calculer la distance focale image f'1 de l’objectif. En déduire et calculer la distance
O1A
permettant de positionner l’objet
afin d'observer une image à l'infini.
1.5. Déterminer la latitude de mise au point, c’est-à-dire la distance séparant les positions extrêmes de l'objet telles que
l'image se trouve dans la zone de vision distincte de l’œil (entre entre la distance minimale de vision distincte δ = 25 cm où
l’œil est au foyer image de l’oculaire et l’infini). Interpréter le résultat obtenu.
1.6. Calculer le grossissement commercial du microscope
G=α'
α
où α' est l'angle sous lequel on voit l'image intermédiaire à
travers l'oculaire et α l'angle sous lequel on voit l'objet placé au punctum proximum (à la distance δ = 25 cm).
DEVOIR SURVEILLÉ N°4

2. Étude quantique du microscope électronique
Le pouvoir de résolution d'un microscope, à savoir la taille des plus petits détails qu'il permet d'observer, est de l'ordre de
grandeur de la longueur d'onde utilisée.
Pour augmenter le pouvoir de résolution d’un microscope, on peut envisager de remplacer les photons par des électrons et
réaliser ainsi un microscope électronique.
Après interaction avec la matière, ces électrons sont récupérés par des capteurs dont les informations permettent de
reconstruire l'image.
2.1. Évaluer l'ordre de grandeur de l'énergie cinétique minimale à communiquer aux électrons sachant que le plus petit détail
que l'on puisse observer sur ce cliché est d'environ 0,1 µm.
Figure 1 – Image d'une tête de fourmi obtenu au Microscope électronique
Données :
➢masse de l’électron me = 9,11.10−31 kg , constante de Planck h = 6,64.10−34 J.s
➢électron-Volt : 1 eV = 1,6.10−19 J
2.2. Quelles limites peut-on prévoir à l’utilisation de faisceaux électroniques plus énergétiques ?
Les limitations évoquées précédemment ont conduit à l’avènement d’une nouvelle famille de microscopes, d’un principe
différent, les microscopes à sonde locale. Les microscopes à sonde locale sont des appareils dont la caractéristique
commune est d’explorer une surface par des déplacements nanométriques d’une sonde au contact ou au voisinage de cette
surface. L’invention du microscope à effet tunnel en 1984 a valu le prix Nobel à G. Binnig et H. Rohrer dès 1986, elle a été
rapidement suivie par l’invention du microscope à force atomique.
Dans le premier cas, la grandeur mesurée est un courant de l’ordre du picoampère (courant tunnel) circulant entre la sonde
et l’échantillon. Dans le second cas, la grandeur mesurée est la force d’interaction entre la sonde et l’échantillon.

Problème 2 : Étude de la délocalisation électronique dans les systèmes conjugués
Il y a plusieurs définitions possibles d'un système conjugué.
Nous utiliserons la suivante : on appelle système conjugué, un ensemble d'atomes ayant des orbitales atomiques pouvant se
recouvrir latéralement et permettant de fortes interactions électroniques entre au moins trois atomes contigus.
Les systèmes conjugués ont une réactivité originale car la délocalisation entraîne une certaine ambiguïté dans la
répartition électronique.
Je vous propose d'étudier la délocalisation électronique dans deux systèmes conjugués : le buta-1,3-diène et le benzène.
Dans ces deux molécules, la chaîne carbonée de la molécule est composée d'une alternance de simples liaisons C-C et de
doubles liaisons C=C permettant aux électrons π par effet mésomère, d'être délocalisés sur l'ensemble de la molécule.
Ainsi le buta-1,3-diène peut être représenté par les formes mésomères limites suivantes :
Figure 2 : Formes mésomères du buta-1,3-diène
Et le benzène :
Figure 3 : Formes mésomères du benzène
1. Confinement d'un électron π dans un puits de potentiel unidimensionnel
Il s'agit dans cette partie de retrouver des résultats essentiels sur le confinement unidimensionnel d'un électron π.
L'électron π , de masse m = 9,11.10-31 kg, est alors assimilé à une particule qui se déplace librement sur un segment de droite,
entre les abscisses x = 0 et x = L. L'énergie potentielle Ep est alors nulle sur le segment et infiniment grande partout ailleurs.
La partie spatiale de la fonction d'onde ψ(x) est alors liée à son énergie totale E par l'équation de Schrödinger des états
stationnaires, à savoir :
−h2
8π2m
(d2Ψ( x)
dx2)=EΨ( x)
où h est la constante de Planck.
On cherche tout d'abord à déterminer la fonction d'onde ψ(x) pour en déduire les valeurs d'énergie possibles.
1.1. Préciser, en les justifiant, les conditions aux limites vérifiées par la fonction d'onde ψ(x).
1.2. Montrer que la solution de l'équation de Schrödinger est de la forme :
Ψ (x)=Bsin(nπx
L)
où n est un entier strictement positif et B une constante d'intégration.
1.3. En utilisant la condition de normalisation que vous justifierez, déterminer l'expression de la constante d'intégration B.
1.4. Déterminer l'expression des niveaux d'énergie En en fonction de m, L, h et n.
1.5. Comment aurait-on pu retrouver ce résultat ? Présenter la démarche et l'analogie utilisée.
1.6. En déduire que le confinement spatial dans la molécule se traduit par une énergie minimale non nulle de l'électron π.
1.7. Ce résultat était-il prévisible ? Retrouver alors cette énergie minimale en utilisant l'inégalité d'Heisenberg.

2. Modélisation du comportement quantique du buta-1,3-diène
En raison de sa grande réactivité, le butadiène est utilisé en synthèse, en particulier dans les réactions de polymérisation :
fabrication de caoutchouc, vernis, nylon...
Je vous propose de modéliser le comportement quantique du buta-1,3-diène en utilisant le modèle d'une boîte quantique
unidimensionnelle où les électrons π sont confinés dans un puits infiniment profond de largeur L.
2.1. Sachant que seuls les deux électrons π sont délocalisés pour chaque double liaison C=C , déterminer le nombre
d'électrons dans la boîte quantique unidimensionnelle formée par le buta-1,3-diène.
2.2. En vertu du principe d'exclusion de Pauli, chaque niveau d'énergie En ne peut être occupé que par deux électrons
possédant des spins anti-parallèles. Comment ces électrons se répartissent-ils dans les niveaux d'énergie ?
Tracer le diagramme d'énergie (ou d'occupation) correspondant.
2.3. Exprimer alors la variation d'énergie ΔE d'un électron π effectuant une transition vers le premier état excité.
2.4. Calculer la longueur d'onde d'absorption correspondant à cette transition.
On donne la longueur (en nanomètres) des différentes liaisons de la molécule dans le tableau ci-dessous :
C-C C=C C-H
0,154 0,134 0,109
3. Modélisation du comportement quantique du benzène
C'est un précurseur important pour la synthèse de nombreux composés organiques : matières plastiques, caoutchoucs,
solvants, plastifiants, détergents, parfums, colorants, additifs alimentaires, médicaments, pesticides, explosifs, etc.
Il est également utilisé comme solvant dans différentes industries, et comme additif antidétonant dans l'essence.
Il est produit par l'industrie pétrochimique essentiellement par reformage catalytique, hydrodésalkylation du toluène et
vapocraquage.
Je vous propose de modéliser le comportement quantique du benzène en utilisant le modèle d'une boîte quantique
bidimensionnelle où les électrons π sont confinés dans un carré de côté a.
Figure 4 : Géométrie du cycle benzénique
Le cycle benzénique est un hexagone régulier plan :
- les six atomes d'hydrogène appartiennent également au
plan du cycle
- les six liaisons C–C sont de longueur identique : 139 pm,
longueur intermédiaire entre celles des liaisons simples
(154 pm) et celle des liaisons doubles (134 pm)
3.1. Calculer le côté a du carré dans lequel on peut inscrire la molécule de benzène.
3.2. En vous appuyant sur les résultats établis dans la 1ère partie, proposer une expression pour les niveaux d'énergie en
fonction de m, L, h et des nombres quantiques nx et ny.
3.3. Tracer le diagramme d'énergie (ou d'occupation) correspondant et faire apparaître les dégénérescences.
3.4. Calculer la longueur d'onde du rayonnement incident pour que la molécule de benzène passe dans son premier état
excité.

Problème 2* : « Quand la lumière dévie les molécules !! »
(Problème inspiré de l'article «Diffraction of Complex Molecules by Structures Made of Light»,Zeilinger, 2001)
Au début du 20ème siècle, Albert Einstein propose de considérer la lumière comme constituée de particules appelées plus
tard photons.
En 1923, L. De Broglie propose de considérer par analogie les particules matérielles comme des ondes.
D’autre part, si la diffraction de la lumière par un réseau est déjà établie depuis le 19ème siècle, Davisson et Germer
montrent qu’effectivement un faisceau de particules massiques, en l’occurrence des électrons, peut être également diffracté
par la matière, validant ainsi l’hypothèse de De Broglie.
Quelques années plus tard, Kapitza et Dirac proposent de tester ces concepts en proposant de faire diffracter un faisceau de
molécules par un réseau…de photons !!
Données :
➢constante de Planck : h = 6,63.10−34 J.s
➢constante d’Avogadro : NA = 6,02.1023 mol-1
➢constante de Boltzmann : kB = 1,38.10−23 J.K−1
➢masse molaire du carbone : MC = 12,0 g.mol−1
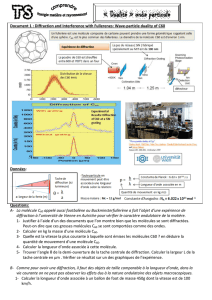
Partie A : Onde de matière associée au fullerène
On s'intéresse dans ce problème aux interférences des ondes de matière associées aux fullerènes, molécules constituées de
60 atomes de carbone et qui possèdent une structure identique à un ballon de football (figure 5).
Figure 5 – Molécule de fullerène Figure 6 – Expérience d’interférences avec des molécules de fullerènes
Le dispositif expérimental est décrit sur la figure 6.
On produit une vapeur de C60 dans un four à une température notée T.
1.1. La vitesse caractéristique des molécules, notée v, est de l’ordre de v = 1,00.102 m.s-1.
Calculer la valeur de la longueur d’onde de De Broglie λDB associée à chaque molécule de fullerène.
1.2. La vitesse typique des molécules de masse m dans un gaz à la température T est de l'ordre de
v=
√
kBT
m
.
En déduire la température du gaz de C60 dans l’expérience considérée.
Le flux de fullerène est envoyé sur un réseau plan de fentes orthogonal à la direction du jet moléculaire (figure 7).
Les fentes ont pour largeur 50 nm et sont chacune distantes de d = 100 nm.
Dans la suite du problème, on étudie la condition d’interférences constructives et on observe la figure d’interférences à une
distance D grande devant d.
2.1. Montrer que les interférences entre les ondes de matière issues des différentes fentes seront constructives dans les
directions vérifiant :
dsin α= pλDB
avec
p∈ℤ
.
Accompagner le raisonnement d'un schéma clair faisant apparaître la différence de marche δ entre deux rayons diffractés
successifs.