TRAITEMENT DU SIGNAL

Spé ψ 2002-2003 page 1/4 Devoir n°1
Spé ψ 2002-2003 Devoir n°1
TRAITEMENT DU SIGNAL
Dans le téléphone, la voix est transformée en signaux électriques par l’intermédiaire
du microphone et d’un filtre passe-bande se trouvant dans le combiné téléphonique. On ob-
tient alors un signal analogique vA(t) qui est transmis jusqu’au premier central par les fils
constituant « la boucle locale ». Les signaux sont ensuite transmis sur le réseau après une
conversion numérique pour permettre leur multiplexage.
Ce problème se propose l’étude simplifiée de certaines étapes de la conversion analo-
gique-numérique décrite par le schéma synoptique suivant :
Ses différentes parties sont présentées dans l’ordre chronologique de la transformation,
sans préjuger de leur difficulté respective. On pourra les traiter dans un autre ordre, sous ré-
serve d’indiquer très clairement la question traitée.
Tous les amplificateurs opérationnels utilisés dans le problème sont décrits par le mo-
dèle idéal, avec des tensions de saturation ±VSAT
Partie I
FILTRE ANTI REPLIEMENT
Le théorème de Shannon prévoit qu’un signal échantillonné à une fréquence fE ne peut
contenir de fréquences supérieures à fE/2 pour que l’information qu’il transporte soit correc-
tement et intégralement transmise. La norme du CCIT* indique fE = 8 kHz pour la bande des
fréquences vocales acceptées [300-3400kHz]. Le signal transmis par la boucle locale pouvant
contenir des fréquences plus élevées, il faut procéder à un filtrage avant de l’échantillonner.
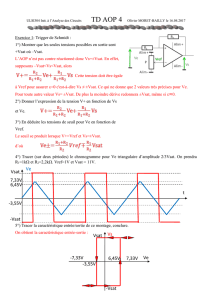
I-1) On considère le montage de la figure 1.
a) Établir l’expression de la fonction de
transfert harmonique . H j
V
V
( )ω = F
A
On posera α = C
C2
1
et ω01 2
1
=R C C .
b) Quelle est la nature du filtre ainsi ré-
alisé ?
* Comité Consultatif International Télégraphique et Téléphonique
t
vA (t)
FILTRE ANTI-
REPLIEMENT
ECHANTILLONNEUR
BLOQUEUR
CONVERTISSEUR
ANALOGIQUE-
NUMERIQUE
MULTI
PLEXAGE
vFvEB vCAN
LIGNE DE
TRANSMISSION
vA
t
v
CAN
+
—
R
R
C1
C2
vA(t)vF(t)
figure 1
N

Spé ψ 2002-2003 page 2/4 Devoir n°1
c) Exprimer l’impédance d’entrée du montage, notée ZE, à l’aide de R, H(jω),
α, ω0 et ω. Conclure.
d) Proposer un montage qui, placé en entrée, permettrait de rendre cette impé-
dance d’entrée infinie quelle que soit la pulsation ω. Indiquer son schéma.
I-2) Pour obtenir la courbe de réponse en amplitude [GdB = 20 log(|H|)) la plus régu-
lière possible, on impose la condition suivante : ω = 0 est solution triple de l’équation
dG
d
dB
ω
= 0.
a)Calculer la valeur correspondante de α dans ces conditions.
b) Donner l’expression correspondante de GdB en fonction de ω
ωC
F
H
G
I
K
J pour cette
valeur particulière de α. Exprimer, en fonction de R et C2, la pulsation de coupure (à –3dB) de
ce filtre et tracer l’allure du diagramme de Bode en amplitude.
Ce type de filtre (avec la valeur particulière de α) est appelé filtre de Butterworth, ici
d’ordre 2. C’est un des deux types utilisés dans les applications technologiques. En télépho-
nie, on utilise des filtres d’ordre 4.
Partie II
ECHANTILLONNEUR-BLOQUEUR
Un montage utilisé peut être celui de la figure 2 :
On suppose que vF varie entre –
V
SAT
2
et
V
SAT
2
.
L’interrupteur KE est un composant électronique commandé par un dispositif non re-
présenté ici. Il se ferme aux instants t0 + kTE (où k est un entier) de manière instantanée, reste
fermé pendant une durée δt très inférieure à TE puis est ouvert le reste du temps.
Montrer que, pour tout t compris entre t0 + kTE et t0 + (k + 1)TE, on a :
vEB(t) = vF(t0 + kTE) +
V
SAT
2
.
Quel est le rôle de la tension
V
SAT
2
appliquée ?
+
—
+
—
+
—
+
—
R
R
R
R
C
R
V
SAT
2
vFv
EB
v1v2
K
E
figure 2

Spé ψ 2002-2003 page 3/4 Devoir n°1
Partie III
ETUDE MATHEMATIQUES DU SIGNAL ECHANTILLONNE
On considère une sinusoïde parfait s(t) = S0 sin(2πf0 t). On suppose pour simplifier que
la fréquence d’échantillonnage est fE = N f0 (pour les applications numériques, on prendra
N = 16).
III-1) L’échantillonnage idéal de s(t) peut être modélisé comme le produit de s(t) par
un signal eECH(t) constitué d’une succession infinie d’impulsions unitaires, apparaissant à la
période TE =
1
fE
..
a) Sachant que la décomposition en série de Fourier de eECH(t) s’écrit
e t f f k f t
k
ECH E E E
( ) cos= +
=
∞
∑
2 2
1
π
b
g
,
établir l’expression du signal échantillonné s*(t) sous la forme d’une somme de fonctions si-
nusoïdales du temps, avec les constantes N, S0, f0 et k.
b) Dans le cas où fE = 16 f0, représenter le spectre en fréquence de s*(t) en se
limitant aux cinq premières raies (fondamental et quatre harmoniques). Indiquer l’amplitude
et la fréquence de chacune de ces raies. Commenter l’allure complète du spectre et la linéarité
de l’opération effectuée.
III-2) Le bloqueur peut être décrit comme un système linéaire dont la réponse impul-
sionnelle b(t) est définie par b(t) = u(t) – u(t – TE) où u(t) représente l’échelon unitaire.
a) Dessiner le graphe de b(t).
b) On définit la transformée de Laplace F(p) d’une fonction f(t) par
F p f t e dt
pt
( ) ( )=−
+∞
z
0
. Quelle est la transformée de Laplace de b(t) ?
c) On obtient la fonction de transfert harmonique d’un système linéaire en po-
sant p = jω dans la transformée de Laplace de sa réponse impulsionnelle. Quelle est la fonc-
tion de transfert harmonique B(jω) du bloqueur ? Montrer qu’elle peut se mettre sous la forme
B j TejT ( ) sinωωωω =
F
H
G
I
K
J×−
222
EE.
d) Établir l’expression de l’argument Φ(ω) de B(jω). En déduire qu’il existe un
retard τ que l’on calculera, entre le signal modèle s(t) et le signal sB(t) issu du bloqueur.
e) Quel est le module B(ω) de B(jω) ? Représenter l’allure du graphe de B(f).
III-3) a) Calculer numériquement l’amplitude du fondamental et des quatre premiers
harmoniques de sB(t).
b) Calculer le taux de distorsion du signal sB(t) définit par
DSSSS
S
=+++
F
H
G
I
K
J
20 2
23 24 25 2
1
log .

Spé ψ 2002-2003 page 4/4 Devoir n°1
Partie IV
CONVERTISSEUR ANALOGIQUE-NUMERIQUE
On étudie ici le principe d’un tel convertisseur dont le schéma est donné sur la fi-
gure 4. Les diodes sont idéales, de tension de seuil nul.
Avant le début de la conversion, l’interrupteur commandé K est fermé et le condensa-
teur est déchargé. Il s’ouvre à la date t0 à laquelle commence la conversion et se referme à
t0 + TE. Durant la conversion, le signal vEB(t0) a une valeur constante comprise entre 0 et VSAT.
IV-1) Étudier la tension aux bornes du condensateur C0 entre les instants t0 et t0 + TE
puis en déduire l’allure de v3(t) entre les mêmes instants. A quelle condition reliant TE, VSAT,
I0 et C0 la conversion est-elle possible ? (A cet étape, la conversion consiste à obtenir une ten-
sion v3 basculant entre VSAT et –VSAT.)
IV-2) Le signal uH(t) est fourni par le circuit de la figure 4 où l’amplificateur opéra-
tionnel n°1 fonctionne en régime saturé. La diode est idéale, de tension de seuil nulle. On
suppose qu’à l’instant t0, uM vient de basculer à la valeur +VSAT.
a) K’ étant ouvert, expliciter uM(t) et représenter sur un même graphe l’allure
de uM(t) et de uC(t).
b) Comment est modifié le fonctionnement précédent si K’ est fermé ? Calculer
alors la période TH de uH(t) en fonction de RH et CH. Dans la suite, on supposera que TH << TE.
IV-3) Comment varie alors v4 dans le montage convertisseur ? Le compteur binaire,
remis à zéro à l’instant t0, enregistre le nombre de basculement de v4 de 0 vers
V
SAT
2
. (On note-
ra que le courant d’entrée dans le compteur est constamment nul.) Montrer qu’après le bascu-
lement de v3 à la valeur zéro, le compteur a en mémoire un nombre proportionnel à la valeur
de vEB(t0). Préciser le coefficient de proportionnalité.
Dans la pratique, un tel compteur est lent et n’est utilisé que dans les appareils de me-
sure (type multimètre numérique). Les convertisseurs utilisés en télécommunication sont plus
performants mais ne peuvent pas être décrits ici.
C
0
+
—
I
0
R
+
—
COMPTEUR
R
K
i = 0
vEB v3v’3v4
uH(t)
V
SAT
2
figure 3
1
2
R
0
R
R
H
R
0
+
—
+
—
CHuH
uM
uC
K
’
figure 4
1
2