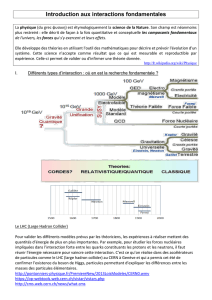
theorie quantique et realite

THEORIE QUANTIQUE ET REALITE
L’idée que le monde est constitué d’objets localisés et dont l’existence ne dépend pas de la conscience
humaine s’avère être incompatible avec certaines prédictions de la mécanique quantique et avec des faits
aujourd’hui établis par l’expérience.
par Bernard d’Espagnat
e critère essentiel auquel doit satisfaire une théorie physique est de conduire à des prévisions
vérifiables. On doit pouvoir monter des expériences dont la théorie prédise les résultats ou dont
elle permette, tout au moins, de calculer les probabilités des divers résultats possibles. De ce point
de vue, la mécanique quantique est pleinement satisfaisante. Cette mécanique, qui constitue à l’heure
actuelle la théorie fondamentale des atomes, des molécules, de l’état solide, du rayonnement
électromagnétique, etc. fournit en effet des méthodes qui permettent d’établir, dans tous ces domaines,
des prévisions vérifiées par les tests expérimentaux.
Toutefois, outre la confirmation expérimentale, on requiert, en général, quelque chose de plus
d’une théorie. On lui demande en effet, non seulement de prédire les résultats des expériences, mais aussi
de procurer une certaine compréhension des processus physiques sous-tendant les résultats obtenus. En
d’autres termes, la théorie ne doit pas seulement fournir la position qu’occupera une aiguille sur un
cadran ; elle doit aussi nous renseigner sur le pourquoi de cette position. Lorsqu’on cherche des
informations de cette espèce dans la théorie quantique, certaines difficultés conceptuelles apparaissent.
Par exemple, en mécanique quantique une particule élémentaire - un électron pour fixer les idées - est
représentée par l’expression mathématique appelée « fonction d’onde », laquelle décrit l’électron comme
s’il était étalé sur toute une région de l’espace.
Cette représentation n’est pas démentie par l’expérience. Au contraire, la fonction d’onde donne
une évaluation exacte de la probabilité pour que l’électron soit trouvé à tel endroit ou à tel autre. Quand
l’électron est détecté il n’est toutefois jamais “étalé” : sa position est toujours bien définie. Dès lors, on ne
voit pas, a priori, de manière tout à fait claire, quelle interprétation physique il convient de donner à la
fonction d’onde, ni non plus quelle image de l’électron on doit se faire. De telles ambiguïtés font que
nombre de physiciens considèrent que l’attitude d’esprit la plus raisonnable consiste à considérer la
mécanique quantique comme un simple ensemble de règles permettant de prédire les résultats des
expériences. Selon cette manière de voir, la théorie quantique ne doit s’occuper que des phénomènes
observables (la position observée de l’aiguille indicatrice sur un écran) et pas du tout de l’état physique
sous-jacent (la position vraie de l’électron).
I se trouve cependant qu’un tel renoncement est encore insuffisant pour lever toutes les difficultés.
Même si la mécanique quantique est considérée comme n’étant rien d’autre qu’un système de règles,
elle est encore en conflit avec une vision du monde que beaucoup d’esprits ont tendance à considérer
comme évidente ou, tout au moins, comme naturelle. Cette vision du monde est fondée sur trois
hypothèses, ou prémisses qui, bien entendu, doivent être acceptées sans preuves. L’une d’elle est le
réalisme, c’est-à-dire la doctrine selon laquelle les régularités observées des phénomènes ont leur origine
dans une réalité physique dont l’existence est indépendante des observateurs humains. La seconde
prémisse pose que l’induction est un mode de raisonnement valable qui peut être utilisé librement pour
tirer des conclusions générales de séries finies de faits. La troisième prémisse est souvent appelée
“séparabilité Einsteinienneé” ou “localité Einsteinienne”; elle pose qu’aucune influence physique
d’aucune sorte ne peut se propager plus vite que la lumière. Les trois prémisses, qui sont souvent
L
I

considérées comme ayant le statut soit d’évidences, soit de vérités bien établies, constituent la base très
générale de tout un ensemble de théories concevables de la nature, que j’appellerai théories réalistes
locales. Un raisonnement découlant de ces prémisses conduit à une prédiction explicite des résultats
d’une certaine classe d’expériences en physique des particules élémentaires. Les règles de la mécanique
quantique peuvent également être appliquées au calcul des résultats de ces expériences. Or, fait
remarquable, les deux prédictions diffèrent ! Dès lors de deux choses l’une : ou bien la mécanique
quantique est fausse ou bien ce sont les théories réalistes locales qui le sont.
Les expériences dont il s’agit furent proposées d’abord en tant qu’ “expériences de pensée”,
conçues seulement pour l’imagination. Au cours des dernières années, cependant, plusieurs versions en
furent réalisées au moyen d’appareils concrets. Bien que les résultats ne soient pas tous en parfait accord,
la majorité d’entre eux vérifient les prédictions de la mécanique quantique et l’on peut maintenant estimer
que – sauf coïncidence extraordinaire qui aurait défiguré les résultats - ce sont les prédictions quantiques
qui seront définitivement confirmées.
Il s’ensuit que les théories réalistes locales sont presque certainement erronées. Les trois prémisses
sur lesquelles ces théories sont fondées sont essentielles pour toute interprétation du monde qui ne fasse
pas violence au sens commun, de sorte que la plupart des esprits ne les abandonnent pas sans réticence. Il
n’en est pas moins vrai que l’une d’elles au moins doit désormais être abandonnée, modifiée, ou
restreinte.
Les expériences portent sur des corrélations entre événements distants et concernent les causes de
ces corrélations. Supposons par exemple que sur deux particules distantes l’une de l’autre de quelques
mètres une certaine quantité physique telle que la charge électrique s’avère avoir la même valeur. Si un
tel fait est observé simplement dans un cas ou deux ou dans un petit nombre de cas, on peut le tenir pour
une simple coïncidence et donc ne pas en tenir compte. Mais si sur un grand nombre de cas semblables la
corrélation se révèle toujours exister, la recherche d’une explication s’impose. Il en irait de même si les
valeurs mesurées étaient toujours opposées au lieu d’être toujours les mêmes. La corrélation serait alors
négative mais sa magnitude serait aussi grande et les chances qu’elle soit due au pur hasard seraient
manifestement aussi faibles.
1. L’ÉTUDE DE CERTAINES CORRÉLATIONS entre événements distants peut conduire à
des conclusions concernant la structure du monde. Prenons un physicien qui met en place une
expérience dans laquelle des particules subatomiques, des protons par exemple, sont propulsés
un par un dans un instrument de mesure : par hypothèse, les valeurs des indications fournies par
celui-ci ne peuvent être que plus ou moins (a). Il constate que pour certains protons le résultat
obtenu est plus et qu’il est moins pour les autres, mais il ne peut dire si l’instrument mesure par
là quelque propriété réelle du proton ou s’il ne s’agit au contraire que de fluctuations dues au
hasard. Le physicien dispose alors deux instruments identiques de part et d’autre d’une source
qui émet deux protons simultanément (b). Il observe une corrélation négative stricte : chaque
fois qu’un instrument affiche plus l’autre affiche moins. De la constatation de cette corrélation,
le physicien infère que c’est une propriété bien réelle du proton qui est responsable des données
affichées et que cette propriété est déterminée dès le moment où les protons sortent de la source.
Si l’échantillon de particules étudié satisfait à certaines conditions requises par la statistique, le
physicien peut même inférer que toute paire de protons émise par la source consiste en un
proton ayant la propriété plus et un autre proton ayant la propriété moins même dans le cas où
aucun de ces protons n’est soumis à la mesure (c). Ces conclusions sont raisonnables si trois
prémisses sont supposées vraies : que certaines propriétés au moins du monde existent
indépendamment de tout observateur humain, que l’induction peut être employée librement et
qu’une mesure effectuée par un instrument ne peut influencer le résultat de la mesure faite avec
l’autre. Une version moins restrictive de cette dernière prémisse n’interdit de telles influences
que si les deux mesures sont si rapprochées dans le temps que l’influence devrait se propager
plus vite que la lumière. Les trois prémisses peuvent être dénommées réalisme, usage libre de
l’induction et séparabilité. La version moins restrictive de la séparabilité est appelée séparabilité
Einsteinienne ou localité Einsteinienne. Toute théorie incorporant ces trois prémisses sera dite
réaliste locale.

Dans tous les cas où une telle corrélation systématique entre événements distants est considérée
comme comprise, dans tous les cas où l’esprit humain se sent autorisé à affirmer que cette corrélation n’a
plus rien de mystérieux, l’explication proposée se réfère toujours à un lien de causalité. Ou bien l’un des
événements est cause de l’autre, ou bien les deux ont une cause commune. Tant qu’un tel lien de causalité
n’a pas été découvert l’esprit ne peut se tenir pour satisfait. Il ne le peut pas (notons ceci, c’est important)
même dans le cas où il existe des règles empiriques - mathématisées ou non, peu importe - qui permettent
de prévoir avec exactitude les futurs effets de corrélation. Une corrélation entre les marées et les phases

de la Lune avait été observée dès l’Antiquité, et des règles de prédiction quantitatives avaient été
formulées, permettant de prévoir l’amplitude des futures marées à partir des données déjà accumulées. Le
phénomène des marées et sa corrélation avec les phases de la Lune ne purent cependant être légitimement
considérés comme compris que du jour où Newton eut exposé sa théorie de la gravitation universelle qui
rendait compte des deux effets par un système de causes communes.
Le besoin d’expliquer les corrélations observées est si puissant qu’une cause commune est souvent
postulée même dans le cas où il n’existe pas d’autres indications en faveur de son existence, que celle
fournie précisément par le fait même de la corrélation. La question de savoir si cette manière de faire peut
toujours être justifiée est centrale dans le conflit entre la mécanique quantique et les théories réalistes
locales. Ces corrélations relient des observations portant sur des particules subatomiques, domaine qui
relève d’une description en termes de physique quantique et comporte toute une difficile problématique
théorique. Les prédictions des théories réalistes locales peuvent toutefois être illustrées en examinant
comment les corrélations entre événements distants sont expliquées dans un contexte plus familier où la
mécanique quantique n’entre pas en jeu.
maginons qu’un psychologue ait inventé un test très simple, auquel tout patient réussit ou échoue, de
sorte qu’il n’y a pas d’ambiguïté dans les résultats. Le psychologue constate que certaines personnes
réussissent et que d’autres échouent, mais il ne possède aucune information sur ce qui peut distinguer
les deux groupes sauf précisément les réponses qu’ils fournissent au test. En d’autres termes, il ne peut
pas dire si le test mesure quelque aptitude ou propriété véritable des patients testés ou si, au contraire, ces
derniers répondent au hasard.
Il ne semble pas que le problème ainsi posé comporte une solution générale ; il pourrait cependant
être résolu au moins dans un cas particulier. Supposons que le test soit administré non plus à une série
d’individus mais à une série de couples mariés, et que leurs réponses fassent apparaître une corrélation
stricte. La manière d’opérer pourra être de séparer les maris et les femmes avant le test et de les soumettre
aux tests un par un dans l’isolement. Quand, plus tard, les résultats sont dépouillés, il se peut qu’on
constate encore qu’une part de la population a réussi alors que l’autre a échoué, mais en ce qui concerne
chaque couple pris un à un, on s’aperçoit que dans tous les cas où le mari a réussi, sa femme a réussi
aussi, et que dans tous les cas où il a échoué, il en a été de même de sa femme.
Si une telle corrélation persiste après que beaucoup de couples ont été testés, le psychologue
conclura très certainement que la réponse de chaque patient individuel au moment où il est testé n’est pas
le pur fait du hasard. Au contraire, cette réponse doit découler de propriétés objectives différant d’un
couple à l’autre et appartenant soit au monde extérieur - si la question du test comporte cette possibilité -
soit, dans le cas contraire, au sujet testé en personne.
La propriété doit déjà être présente avant le test et, si elle appartient au sujet et non pas au monde
extérieur, elle doit en fait lui avoir appartenu, sous une forme ou sous une autre, dès avant la séparation.
Assurément, le hasard peut éventuellement avoir alors joué un rôle dans le développement, chez chaque
individu, de la propriété dont il s’agit, mais une telle influence doit s’être exercée avant la séparation des
couples. C’est seulement lorsque mari et femme étaient ensemble qu’ils ont pu acquérir des traits
communs susceptibles ensuite de les faire réagir de la même manière. Ainsi, quelle que soit la nature de la
question, la corrélation est donc expliquée par le fait qu’elle résulte d’une cause commune antérieure au
test : en bref, les réponses ne sont pas données au hasard.
Une autre explication, a priori possible, et qu’il convient d’éliminer pour pouvoir vraiment faire la
déduction qui précède, consisterait à attribuer la corrélation observée au fait que maris et femmes ont pu
échanger des informations au moment même où ils subissaient le test. Si quelque moyen de
communication leur était alors accessible, il n’y aurait en effet aucune nécessité à invoquer l’existence
préalable d’une propriété quelconque, déterminant les réactions des individus et distinguant les couples
les uns des autres avant le test. Celui des époux qui subirait le test le premier pourrait choisir au hasard sa
réponse et la communiquer à son partenaire en priant ce dernier de répondre la même chose, ce qui
induirait bien la corrélation observée. Lors d’une expérience conduite au moyen de vrais tests
psychologiques il ne serait pas difficile de se prémunir contre des subterfuges de cette espèce. A la limite,
I

les tests pourraient être faits à des instants si voisins l’un de l’autre, ou encore le mari et la femme
pourraient les subir en des lieux si éloignés qu’aucun signal de vitesse égale ou inférieure à celle de la
lumière ne pourrait arriver à temps pour être d’une efficacité quelconque.
ne fois qu’il s’est bien convaincu par l’argument qu’on vient d’expliciter, du fait que le test
mesure des propriétés qui préexistent au test même, le psychologue peut faire un pas de plus dans
le raisonnement en utilisant l’induction. Si les couples déjà testés constituent un échantillon
représentatif d’une certaine population de couples et si l’échantillon en question satisfait à certaines
conditions statistiques standard, le psychologue peut inférer par induction que n’importe quel couple
choisi dans cette population sera constitué d’un mari et d’une femme qui, soit ont tous les deux, soit
n’ont, ni l’un ni l’autre, la propriété mesurée par le test. Par le même argument, il peut conclure que dans
n’importe quel échantillon, représentatif et de taille suffisante, composé de couples déjà séparés mais qui
n’ont pas encore été testés (ou qui ne le seront jamais), certains ont la propriété et les autres non. Le degré
de vraisemblance de telles assertions se rapproche de plus en plus de la certitude au fur et à mesure que la
taille des échantillons augmente. Ainsi, l’existence d’une corrélation stricte au sein de chaque couple et
celle de différences objectives entre certains couples sont toutes deux inférées par induction à partir des
données expérimentales, même pour des échantillons de la population de couples qui n’ont été soumis à
aucun test.
Ces conclusions reposent sur les trois prémisses qui servent de base aux théories réalistes locales.
Le réalisme est une hypothèse qui s’impose dès que l’on exige que certains tests au moins soient relatifs à
des propriétés existant indépendamment de l’observateur. Il a été nécessaire de postuler la validité
générale de l’induction afin de pouvoir extrapoler certaines conclusions, fermement établies au sujet des
couples observés, à ceux des couples qui ne le sont pas, ou pas encore. La séparabilité enfin a été
incorporée dans l’hypothèse que, lors du test, les maris et les femmes ne peuvent communiquer. Si les
tests sont administrés quasi-simultanément, de telle sorte que tout signal échangé entre époux devrait,
pour être utile, se propager plus vite que la lumière, l’hypothèse est équivalente à celle de la séparabilité
Einsteinienne.
A première vue, les conclusions tirées ci-dessus de cette expérience hypothétique de psychologie
semblent découler incontestablement des faits. Certains épistémologues pourraient cependant les mettre
en doute. En particulier, un épistémologue bien averti des fondements de la mécanique quantique pourrait
soutenir qu’il n’y a pas de nécessité logique qui nous contraigne à accepter les trois prémisses des
théories réalistes locales et que, par conséquent, il n’y en a pas davantage à accepter les deux conclusions
qui en dérivent : ni celle selon laquelle une corrélation existait entre hommes et femmes dès avant le test
ni non plus celle selon laquelle des différences existaient entre les couples d’un même échantillon avant le
test. Notre psychologue trouvera sans aucun doute que de telles objections sont ridicules. Il estimera
qu’elles expriment un doute injustifié et il jugera qu’elles ne font que révéler un goût du paradoxe très
éloigné du véritable esprit scientifique. Dans la littérature consacrée aux principes de la mécanique
quantique, on trouve cependant beaucoup d’arguments implicitement fondés sur ce type d’observations et
qui visent tous à montrer que, en particulier, les différences, entre couples dont il était question plus haut,
n’existent pas nécessairement avant qu’elles ne soient mesurées.
Un trait très caractéristique de la mécanique quantique est que ses prédictions n’indiquent
d’ordinaire que la probabilité d’un événement et non pas l’affirmation déterministe que l’événement aura
lieu ou n’aura pas lieu. La fonction d’onde qui sert à décrire le mouvement d’une particule est interprétée
en général d’une manière probabiliste : la probabilité de trouver la particule en un lieu donné est
proportionnelle au carré de la valeur de la fonction d’onde en ce point. Comme je l’ai dit plus haut, une
fonction d’onde est parfois étalée sur une région assez vaste, ce qui implique que les probabilités sont
elles aussi distribuées de la sorte. Bien entendu, quand nous faisons une mesure en un point de notre
choix, il faut bien que la particule y soit détectée ou non. On dit alors que la fonction d’onde est réduite.
La question intéressante du point de vue épistémologique est alors : “est-il vrai ou non d’affirmer que la
particule possédait déjà cette position avant que la mesure ne soit faite ?”
U