PSI* 15-16 TD Physique N°2 – ALI

PSI* 2015 – 2016 1 TD N°2
PSI* 15-16
TD Physique N°2 – ALI
EXERCICE 1 : Amplificateur différentiel à haute impédance d’entrée
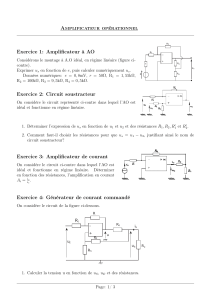
Soit le circuit ci-dessous :
e1
e2
R1
R2
R3
R4
s
+
+
_
_
A.O. 1
A.O. 2
s1
A
i
1. Exprimer la tension de sortie s en fonction des tensions d'entrées e1, e2 et des résistances R1,
R2, R3 et R4.
2. Quelle valeur doit-on donner à la résistance R3 pour que le circuit réalise un amplificateur de
différence ?
3. Comment peut-on effectuer expérimentalement le réglage de la résistance R3 ?
4. Sachant que R1 = 90 k, déterminer alors la valeur des autres résistances afin d'avoir une
amplification différentielle
10
ee s
A12
d
.
5. Quelle est la résistance différentielle d'entrée Rde de cet amplificateur et quelle est sa
résistance de sortie Rs ? Commenter les valeurs de ces résistances.
EXERCICE 2 : Simulation d’une bobine parfaite
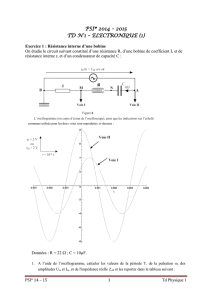
Analyser chacun des deux blocs suivants vus de l’entrée et déterminer comment les associer pour
réaliser une inductance simulée ; quel(s) avantage(s) et/ou inconvénient(s) présentera-t-elle par
rapport à une bobine réelle ?
L’AO fonctionne en régime linéaire
R2
u

PSI* 2015 – 2016 2 TD N°2
EXERCICE 3 : Dérivateur
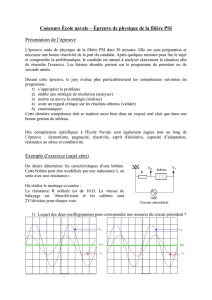
On considère le circuit ci-dessous :
_
+
ve
vS
R
C
montage 1
1. Calculer la fonction de transfert du montage 1 si l’amplificateur opérationnel est réel de gain
en boucle ouverte µ0 et de constante de temps fC ; on fera les approximations liées aux
valeurs numériques : R = 10 k, C = 100 nF, µ0 = 105 et fC = 10 Hz
Déterminer les grandeurs caractéristiques de la fonction de transfert du montage.
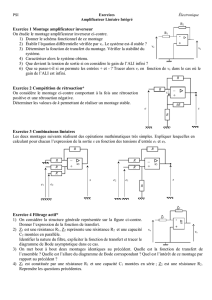
La forme obtenue permet-elle d’interpréter la courbe suivante correspondant à la réponse
du montage à un signal triangulaire de fréquence 100 Hz :
vS
temps (ms)
2. On réalise le montage 2. On choisit R’ = 250 , . La fonction de transfert s’écrit alors :
2
0
'1
)(
µ
RC
CRj
RCj
jH
C
, en tenant compte des valeurs numériques.
Le facteur de qualité vaut alors Q’ = ½. Quelle est maintenant l’allure de la réponse à un
signal triangulaire de fréquence 100Hz ?
montage 2
ve
_
+
vS
R
C
R’

PSI* 2015 – 2016 3 TD N°2
EXERCICE 4 : Filtre de Sallen et Key – Stabilité
L’ALI fonctionne en régime linéaire et est supposé idéal
1. Exprimer, en utilisant la figure 5., la fonction de transfert de ce filtre en fonction des
admittances 
 et du coefficient réel k.
2. Avec la figure 6., mettre cette fonction sous forme canonique en explicitant les
caractéristiques du filtre.
3. Etudier la stabilité du comportement linéaire du filtre en fonction du coefficient k.
EXERCICE 5 : Etude d’un détecteur d’objets ferromagnétiques
Le montage ci-dessous correspond à un détecteur d’objets dont le problème se propose de faire
l’analyse par blocs fonctionnels.
1. Oscillateur
+15 V

PSI* 2015 – 2016 4 TD N°2
Le bloc étudié permet d’observer dans certaines conditions une tension sinusoïdale en M.
D’où provient l’énergie nécessaire à l’existence de cette tension ?
On donne la fonction de transfert de la chaîne de retour :
  = 4
(4
+4  )+1+4 +4  (3+1/( ))
Exprimer la condition nécessaire correspondant à une oscillation sinusoïdale (on admettra qu’elle
est suffisante).
De cette condition déduire la valeur que doit posséder A = 1 + 2
1 en fonction des autres
résistances du montage, ainsi que la pulsation 0 des oscillations ; réaliser les AN pour :
R1 = 680  ; R3 = 3300 R’4 = 2700  R’’4 = 330 CnF
2. Capteur inductif – Amplificateur sélectif
On veut que la fréquence de résonance de ce circuit soit la fréquence trouvée en 1. ; déterminer
littéralement et numériquement C0.
Lorsqu’un objet ferromagnétique passe devant la bobine, son inductance augmente et devient
L = L0( 1 + ), avec  << 1. Exprimer 4
2 au premier ordre en .
3. Sommateur
On rappelle que Q = R0/(L00).

PSI* 2015 – 2016 5 TD N°2
4. Cellule de détection
La tension appliquée, v5 est sinusoïdale d’amplitude V5 calculée au 3. en présence d’un objet.
On donne R7 = 6,8 Met C2 = 1 µF ; la diode est idéale ; montrer que l’on a pratiquement v6 = 2,5 V.
5. Comparateur
Toujours en présence de l’objet, déterminer v7
On suppose que l’on supprime l’objet ferromagnétique à t = 0.
Déterminer alors v6 en fonction du temps. Au bout de combien de temps la tension v7 bascule-t-elle ?
Ce dispositif peut-il servir à compter des objets ferromagnétiques distants de 50 cm et se déplaçant à
1 m/s ?