Potentiel quantique variable Notes de cours - Alain Le Rille

x= 0
x
V(x)
V0
x
V(x)
−V0
−a
2
a
2
x
V(x)
V0
0`
~v =v ~uxV(x) = V0
B˜ ψ(x, t) = ϕ(x)e−iE
~t
E > V0
BE < V0
BV0→ ∞
◦

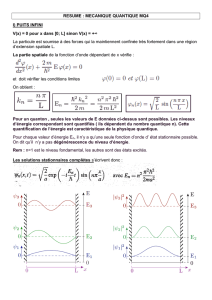
~v =v ~uxx→ −∞
x= 0 x < 0V(x)=0 x > 0V(x) = V0>0
E > V0
B˜ ψ(x, t) = ϕ(x)e−iE
~t
Bϕ(x)dϕ
dx
B~ J=|˜ ψ(x, t)|2~~
k
m
R T
~v =v ~uxx→ −∞
x= 0 x < 0V(x)=0 x > 0V(x) = V0>0
E < V0
B˜ ψ(x, t) = ϕ(x)e−iE
~t
Bϕ(x)dϕ
dx
B~ J=|˜ ψ(x, t)|2~~
k
m
R T
x
V(x)
V0
˜
Aiei k1xe−i ω t
˜
Are−i k1xe−i ω t
E < V0
˜
Ate−ρ2xe−i ω t
R= 1
E > V0
˜
Atei k2xe−i ω t
0< R < 1 0 < T < 1
◦

E > V0E < V0
EV0R→0V0→ ∞
m
x < −a
2V(x) = V0>0
x∈−a
2; +a 2V(x)=0
x > a
2V(x) = V0>0
E < V0
Bk
k0
Bϕs(x)ϕa(x)
B
k0=ktan k a
2
k0=−k1
tan(k a
2)
B
αk a
2=
cos k a
2
cos k a
2sin k a 2>0
αk a
2=
sin k a
2
cos k a
2sin k a 2<0
α
sin k a
2|sin k a 2|cos k a 2|cos k a 2|αk a 2
k a
2
y
sin k a
2
cos k a
2
αk a
2
k1a
2
k3a
2
k5a
2
k4a
2
k2a
2
◦

V0= 3,5~2
m a2
V0−E
•
•
•δ=~
√2m(V0−E)
•
~v =v ~uxx→ −∞
x= 0 x=`
x < 0V(x)=0
x∈[0; `]V(x) = V0>0
x > ` V (x)=0
E < V0
B˜ ψ(x, t) = ϕ(x)e−iE
~t
Bϕ(x)dϕ
dx
◦

E
V0> E `
ρ ` =√2m(V0−E)
~`1
T≈16 E(V0−E)
V2
0
e−2ρ `
α
α r
α
α
R V0
r
V(x)
E
`
−V0
R
Eb
α
BEnα R
f
P≈16 E(Eb−E)
V2
0
e−2ρ `
ρ ` =√2m(Eb−E)
~`1
◦