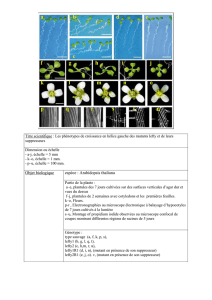
I DYNAMIQUE DES ELECTRONS DE BLOCH 2 2 I.1.1 3 I.1.2 4 I.1.3

I DYNAMIQUE DES ELECTRONS DE BLOCH 2
I.1 MODELE SEMI-CLASSIQUE: 2
I.1.1 DEMONSTRATION DES EQUATIONS SEMI – CLASSIQUES : 3
I.1.2 THEOREME DE LA MASSE EFFECTIVE: 4
I.1.3 VALIDITE DE L'HYPOTHESE SEMI-CLASSIQUE: 7
I.2 MOUVEMENT DANS UN CHAMP ELECTRIQUE UNIFORME ET CONSTANT: 8
I.3 MOUVEMENT DANS UN CHAMP MAGNETIQUE UNIFORME ET CONSTANT: 9
I.3.1 UTILISATION DE B POUR DETERMINER LES PROPRIETES DE LA MATIERE. 10
II EQUATION DE BOLTZMANN: 11
II.1 FONCTION DE DISTRIBUTION DES ELECTRONS. 11
II.2 EQUATION DE BOLTZMANN: 11
III APPROXIMATION DU TEMPS DE COLLISION 12
III.1 HYPOTHESE DE L’EQUILIBRE LOCAL: 12
III.2 LINEARISATION: 12
III.3 VECTEURS DENSITE DE COURANT ELECTRIQUE ET DE FLUX DE CHALEUR: 13
III.4 ELECTRONS ET TROUS: 15
III.5 PHENOMENE DE CONDUCTION DANS LES METAUX: 16
III.5.1 APPLICATION A LA CONDUCTION ELECTRIQUE: 17
III.5.2 APPLICATION A LA CONDUCTIVITE THERMIQUE 19
III.5.3 EFFETS THERMOELECTRIQUES 21
III.6 PHENOMENE DE CONDUCTION DANS LES SEMI – CONDUCTEURS: 21
III.7 TRANSPORT SOUS CHAMP MAGNETIQUE 24
III.7.1 EFFET HALL 25
III.7.2 MAGNETORESISTANCE 26
IV ECRANTAGE 27
IV.1 CONSTANTE DIELECTRIQUE GENERALISEE 27
IV.2 ECRANTAGE DANS L'APPROXIMATION DE THOMAS - FERMI 27
IV.2.1 CAS DES METAUX: 28
IV.2.2 CAS DES SEMI – CONDUCTEURS: 29

Transport électronique
Précédemment, nous avons vu quelques modèles classiques et simples, comme les modèles
de Drude et de Sommerfeld.
Nous allons ici effectuer un traitement quantique du problème, ou plutôt semi-classique.
I Dynamique des électrons de Bloch
I.1 Modèle semi-classique:
En mécanique quantique, les électrons ne peuvent plus être considérées comme des
particules ponctuelles avec une position et une vitesse bien définies, et ceci en raison des
inégalités d'Heisenberg.
On va alors représenter la particule par un paquet d'ondes planes afin de se rapprocher d'un
modèle semi-classique.
(1)
(
)
(
)
(
)
∫−
=k
ti
kn
nkderkar n
rr
r
r
r
r
ω
ψψ
,
où les
(
)
(
)
rki
knkn erur
r
r
rr
r
r
.
= ψ sont les fonctions de Bloch correspondant à l'énergie d'une
bande kn
Er, et h
r
rkn
kn
E
= ω
, ceci afin que l'on ait bien
t
iH
∂
∂
=
ψ
ψ h.
Si l'on impose aucune action extérieure, le paquet d'onde est stable et
(
)
tcsteka ∀=
r
.
Par ailleurs, pour respecter la réalité physique, le paquet d'onde va être centré sur une
valeur 0
k
r
.
Avec
(
)
PZBtaillek
<<
∆
.
Quelle est alors l'extension de ce paquet d'onde dans
l'espace réel?
On a:
(2)
(
)
(
)
(
)
(
)
∫−
=+ k
tRki
kn kderkatRr n
r
r
r
r
r
r
r
r
r
ω
ψψ
.
00 ,
Le terme en
(
)
(
)
0
rka kn
r
r
r
ψ a toujours une extension
caractéristique dans l'espace réciproque de k
r
∆, puisque à 0 r
r
fixé, il n'y a aucune raison pour
que knr
ψ
varie énormément avec k
r
(le paquet d'onde dans l'espace réciproque est donné par la
fonction
(
)
ka
r
).
D'après les propriétés de la transformée de Fourier, l'extension spatiale de la fonction
d'onde se fera donc autour de 0
r
r
avec une largeur s'étendant sur plusieurs mailles
élémentaires. En effet,
( )
.
1élemmaille
PZBk >>>
<<
.
On va donc repérer l'électron par le centre du paquet d'ondes, que l'on appellera
abusivement "position" de l'électron, et le caractère non localisé de la particule se manifestera
dans l'extension de ce paquet d'ondes.
Ceci se comprend si l'on calcule la vitesse de groupe de ce paquet d'onde:
∆

(3) 0
0
,
1
knkn
kkk
kn
k
gvEgradgradv rr
rrr
r
r
h
r=== =
ω
C'est cette extension que la modèle semi-classique vise à décrire, et il s'applique à des
champs peu variables à l'échelle du paquet d'ondes et donc variable très lentement à l'échelle
de la maille élémentaire.
Le modèle semi classique se fonde sur l'hypothèse qu'il n'y pas de transitions interbandes,
et le fait que les champs soient lentement variables à l'échelle de la maille élémentaire
implique, ce que nous allons démontrer, les relations suivantes:
(4) kn
k
kn Egradv
dt
rd r
r
r
h
r
1
==
(5)
[ ]
BvEe
dt
kd ln
r
r
r
r
h∧+−= ,
où
r
r
est la "position" de l'électron, c'est-à-dire le centre du paquet d'onde dans l'espace
réel, et k
r
hest la "quantité de mouvement" de l'électron, c'est-à-dire que k
r
est le centre du
paquet d'onde dans l'espace réciproque.
I.1.1 Démonstration des équations semi – classiques :
1ère étape: Montrons que si on a knknkn EH rrr
ψ
ψ
=
, alors il existe une fonction
(
)
∇−
r
iEn, ne
dépendant que de la quantité de mouvement de l'électron, telle que
(
)
knknkn
nEiE rrr
r
ψψ =∇− .
On a kn Er qui est une fonction périodique avec la périodicité du réseau réciproque. On peut
donc la décomposer en série de Fourier:
(6)
(
)
∑
∈
=..
.
~
BRR
Rki
Rn
neEkE r
r
r
r
r
,
soit:
(7)
(
)
∑
∈
∇
=∇− ..
.
~
BRR
R
Rn
neEiE r
r
r
r
r
, avec R
grad r
r
=∇ .
Or
( )
....
....
2
1
.1 2
.
y
R
x
R
RRe
yx
kn
knkn
R
∂
∂
+
∂
∂
+=
+∇+∇+=
∇
ψψ
ψ
ψψ
r
rr
rr rrrr
(
)
Rr
kn
r
r
r+=
ψ . (Développement de Taylor)
D'après les propriétés des fonctions de Bloch, on a donc
(
)
ree kn
RkiR
r
r
r
r
r
r
ψ
.. = ∇
Ce qui permet de démontrer le résultat de la première étape:
(8)
(
)
(
)
knkn
BRR kn
Rki
nEeEiE rr
r
r
r
r
r
ψψ ==∇−
∑
∈..
.
~
Ceci constitue un résultat fondamental. En effet, l'équation aux valeurs propres écrite ci-
dessus à directement la forme de celle d'un électron libre, mis à part que l'hamiltonien n'est
pas l'énergie cinétique de la particule : le champ cristallin n'apparaît plus que dans la relation
de dispersion.

2ème étape : résolution de l'équation aux valeurs propres.
Nous allons ici nous limiter au champ électrique, le traitement pour le champ magnétique
étant le même bien qu'un peu plus calculatoire.
On a donc
(9)
( ) ( )
t
itrUH
∂
∂
=+
ψ
ψ h
r,, avec EeUgrad
r
=
L'hypothèse que nous faisons alors est qu'il n'y a pas de transition interbandes.
En utilisant (1), l'équation aux valeurs propres se réécrit:
(10) ( ) ( ) ( )
t
itrUkdtrHta
kknk
∂
∂
=+
∫
ψ
ψψ h
r
r
r
rrr ,,
Or
(
)
kn
n
knknkn iEEH rrrr
r
ψψψ ∇−== , d'après (8). On peut donc écrire:
(11)
(
)
[
]
( )
t
itrUiEn
∂
∂
=+∇−
ψ
ψ h
r
r
,
Dans un cadre classique, on aurait :
(12) p
H
t
rr
r
∂
∂
=
∂
∂
et r
H
t
pr
r
∂
∂
−=
∂
∂
.
Etant alors données les dépendances en
r
r
et en p
r
des divers termes de (11), ceci s'écrit:
(13) p
E
t
rn
r
r
∂
∂
=
∂
∂ et Ee
r
U
t
p
r
r
r
−=
∂
∂
−=
∂
∂
Si on repasse alors en mécanique quantique, on a:
(14) k
E
p
E
dt
rd nn r
h
r
r
∂
∂
=
∂
∂
=1, ainsi que:
(15) Ee
t
kr
r
h−=
∂
∂
I.1.2 Théorème de la masse effective:
Considérons une bande n comportant un extremum de bande 0
k
r
.
Toute fonction de Bloch dans cette bande s'écrit:
(16)
(
)
rki
knkn eur
r
r
rr
r
.
= ψ
Mais si k
r
est voisin de 0
k
r
, alors on a
(17)
(
)
0
0
0
.kn
rkki
kn
rki
kn eue r
r
r
r
r
r
r
r
ψψ
−
== .
La fonction d'onde totale dans le modèle semi-classique s'écrit donc, d'après (1):
(18)
(
)
(
)
(
)
(
)
rFkdetatr kn
k
rkki
kkn
r
r
r
r
r
r
r
r
r
rr ., 0
0
0
ψψψ == ∫−,

où
(
)
(
)
(
)
∫−
=k
rkki
kkdetarF r
r
r
r
r
r
r
r
0 est très lentement variable en
r
r
dans la mesure où 0 kk
r
r
− est
petit.
Par ailleurs, on a
(19)
(
)
(
)
(
)
(
)
(
)
( ) ( ) ( )
( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
trFeREr
etrFeREr
ertRrFRE
RrtRrFRE
rtrFeREtrFiE
BRR
RiRki
n
kn
BRR
rki
R
n
kn
BRR
rki
kn
n
BRR kn
n
BRR kn
R
n
kn
n
,
~
,
~
,
~
,
~
,
~
,
..
..
..
.
.
..
.
..
..
.
0
0
0
0
0
0
0
00
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
rrr
r
r
r
r
r
rr
r
r
r
r
r
r
r
r
r
r
r
r
=
=
+=
++=
=∇−
∑
∑
∑
∑
∑
∈
∇−
∈
∇
∈
∈
∈
∇
ψ
ψ
ψ
ψ
ψψ
On a donc :
(20)
(
)
(
)
(
)
(
)
trFikEtrFiE n
knkn
n,, 0
00
r
r
r
r
r
rr ∇−=∇−
ψψ
D'où, en injectant le résultat précédent dans l'équation de Schrödinger (11), on obtient:
(21)
(
)
(
)
( )
t
F
itrFUikEn
∂
∂
=+∇− h
r
r
r
,
0
Si maintenant on effectue un développement de
(
)
kEn
r
autour de 0 k
r
, on obtient, puisque
n
E présente un extremum en 0 k
r
:
(22)
(
)
(
)
(
)
2
0
2
0
*
2
kk
m
kEkE nn
rr
h
rr −+= ,
où *m est appelée masse effective, et correspond au terme qui apparaît dans le
développement. En appliquant ce résultat à ∇−=
r
r
r
ikk 0, on obtient une nouvelle expression
de l'équation de Schrödinger:
(23)
( ) ( )
t
F
itrFU
m
kEn∂
∂
=
+∇− h
r
r
h
r,
*2 2
2
0
ce qui signifie physiquement que à un extremum de bande, on va pouvoir étudier les
particules comme des particules libres de masse effective *m.
Remarque: lien entre masse effective et structure de bande:
On se souvient que, pour des fonctions des fonctions de Bloch de la forme
(
)
(
)
rki
knkn erur
r
r
rr
r
r
.
= ψ , la fonction u était solution de l'équation:
(
)
(
)
ruEruh knknknk
r
r
rrrr
=
, avec
(
)
( )
rVik
m
hk
r
r
r
h
r+∇−= 2
2
2
, V représentant le champ cristallin.
On avait par ailleurs:
(24)
(
)
kkdk hkdik
m
dk
m
hrrr
r
r
r
hh +∇−+=
+
2
2
2
2
,