OF-5674: Residual Total Magnetic Field Descriptive notes Data

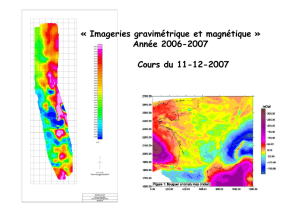
OF-5674: Residual Total Magnetic Field
Descriptive notes
Data used to make this map were acquired from regional aeromagnetic surveys flown between 1952 and
1962 for the Geological Survey of Canada. Their specifications are listed below. Initially, magnetic data
were compiled and contoured manually. The contour maps were later transformed into a digital format using
magnetic field values determined at the intersections of the flight lines and the contours (Dods et al., 1985).
Data from each individual survey were interpolated at an interval of 200 m on a square grid using the
minimum curvature algorithm (Briggs, 1974). The data from the survey flown over Lake Athabasca at a
height of 150 m were upward continued to the same height as the other surveys. Each grid was then
micro-levelled to remove directional effects along flight lines (Minty, 1991). Filtering was done in the
frequency domain and the maximum micro-levelling correction applied to the data was 10 nT. There is no
overlap between adjacent surveys and therefore the grids could not be merged directly. A new data set was
obtained by interpolating the data from the micro-levelled grids at the location of the original digitised points.
These data were then interpolated at a 200 m interval to obtain the final map presented here. Survey seams
may be visible in derivative products calculated from this map because there is no overlap between the
surveys.
OF-5674: Composante résiduelle du champ magnétique total
Notes explicatives
Les données utilisées pour produire cette carte ont été acquises à partir de levés aéromagnétiques
régionnaux effectués de 1952 à 1962 pour la Commission géologique du Canada. Leurs spécifications sont
données plus bas. Initialement, les données magnétiques furent compilées et contourées manuellement. Les
cartes d=isovaleurs furent par la suite numérisées en déterminant la valeur du champ magnétique aux
intersections des lignes de vol et d=isovaleurs (Dods et coll., 1985). Les données de chacun des levés ont
été interpolées sur une grille carrées de 200 m de côté à l=aide de l=algorithme de la courbure minimum
(Briggs, 1974). Les données du levé volé au dessus du lac Athabasca à une hauteur de 150 m ont été
prolongées vers le haut à la même hauteur que les autres levés. Chaque grille à par la suite été micro-nivelée
pour enlever les effets directionnels le long des lignes de vol (Minty, 1991). Le filtrage a été fait dans le
domaine des fréquences et la correction maximum de micro-nivellement appliquée aux données a été de 10
nT. Il n=y a aucune superposition entre les grilles et celles-ci ne purent donc être directement assemblées. Un
nouveau jeu de données a été obtenu en interpolant des données à partir des grilles micro-nivelées à la
localisation originale des données numérisées. Ces nouvelles données ont alors été interpolées à un
espacement de 200 m pour obtenir la présente carte. Les joints entre les levés peuvent être visibles sur des
produits dérivés calculés à partir de cette carte car il n=y a pas de superposition entre les levés.
References / Références
Briggs, I. C.,1974, Machine contouring using minimum curvature: Geophysics, 39 , no.1, 39-48.

Dods, S. D., Teskey, D. J., and Hood, P. J.,1985, The new series of 1: 1 000 000-scale magnetic anomaly
maps of Canada: Compilation techniques and interpretation; in Ed. W. J. Hinze: The utility of
regional gravity and magnetic anomaly maps, Society of Exploration Geophysics, 69-87.
Minty, B. R. S.,1991: Simple micro-levelling for aeromagnetic data (short note): Exploration Geophysics,
22, no.4, 591-592.

OF-5675: Residual Total Magnetic Field Draped to Basement Topography
Descriptive notes
The sandstones of the Athabasca Basin are as much as 1.7 km thick. The sandstones are non magnetic and
do not affect the magnetic field. However, magnetic anomalies originating from the Precambrian basement
under the basin are attenuated relative to anomalies from outside the basin. It is possible to mathematically
drape the data to a smooth surface that is about 300 m above the basin basement, i.e., the average flight
height of the survey. Here, a simple Taylor series expansion has been used (Grauch, 1984; Pilkington and
Roest, 1992). Basement topography was obtained by combining depths to basement from seismic data
(Hobson and MacAulay, 1969) and drillhole data (Slimmon, 2006). These data were gridded to the same
grid spacing as the magnetic data and the resulting grid was smoothed to remove high frequency noise. The
Taylor series expansion was limited to two terms, the first and second vertical derivative of the
micro-levelled residual total magnetic field. Vertical derivative grids from the different survey blocks were
individually micro-levelled (Minty, 1991) to remove directional noise in the direction of the flight lines. They
were then merged to obtain continuous grids of the first and second vertical derivative of the magnetic field.
These grids and the micro-levelled residual total magnetic field were used to compute the Taylor series
expansion. The resulting map is an approximation of what the magnetic field would be if it had been
measured at a height of 300 m above the Precambrian basement. There are two limiting factors to this
approximation. Firstly, the exact topography of the basin is uncertain, boreholes tend to be concentrated
along basin edges within the shallowest parts of the basin, and there were only a few seismic lines crossing
the deeper portion. Secondly, Taylor series expansion is normally limited to small distances. Here, in the
central part of the basin, distances are well in excess of 1 km.
This map allows easier recognition of basement features that are difficult to see in the standard non-draped
map of the magnetic field, especially in the central and deepest part of the basin. Small amplitude high
frequency (short wavelengths) noise is also visible, but can be easily distinguished from the geological signal.
This noise is due to the use of first and second vertical derivatives of the magnetic field in the Taylor series
expansion which tend to amplify any noise present in the data. This map should therefore only be used for
qualitative interpretation.
OF-5675: Composante résiduelle du champ magnétique total drapée sur une surface moulant la
topographie du socle
Notes explicatives
L=épaisseur des grès du Bassin de l=Athabasca atteint 1.7 km. Les grès son non magnétiques et n=influencent
pas le champ magnétique. Cependant, les anomalies magnétiques ayant leur origine dans le socle
précambrien sous le bassin sont atténuées par rapport à celles de l=extérieur du bassin. On peut
mathématiquement draper les données sur une surface lisse à environ 300 m au dessus du socle sous bassin,
i.e. à la hauteur moyenne de vol du levé. Dans le cas présent, une simple expansion en série de Taylor a été
utilisée (Grauch, 1984; Pilkington et Roest, 1992). La topographie du socle a été obtenue en combinant des

profondeurs provenant de données sismiques (Hobson et MacAulay, 1969) et de forages (Slimmon, 2006).
Ces données on été interpollées au même espacement que les données magnétiques et la grille a été lissée
pour enlever le bruit de hautes fréquences. L=expansion en série de Taylor a été limité à deux termes, les
dérivées verticales première et seconde du champ magnétique résiduel micro-nivelé. Les grilles des dérivées
verticales de chacun des levés ont été micro-nivelées (Minty, 1991) pour enlever le bruit dans la direction
des lignes de vol. Elles on ensuite été assemblée pour obtenir des grilles continues des dérivées verticales
premières et secondes du champ magnétique. Ces grilles et le champ total résiduel micro-nivelé ont été
utilisées pour calculer l=expansion en série de Taylor. La carte résultante est une approximation de ce
qu=aurait été le champ magnétique s=il avait été mesuré à une hauteur de 300 m au dessus du socle
précambrien. Il y a deux facteurs limitant la validité de cette approximation. Premièrement, la topographie
exacte du bassin est incertaine, les forages étant situés près de sa bordure, là où il est moins profond, et il
n=y a que quelques lignes sismiques. Deuxièmement, une expansion en série de Taylor est limitée aux faibles
distances. Ici, la partie centrale du bassin va au delà de 1 km.
Cette carte permet de plus facilement identifier des structures du bassin qui sont difficiles à voir dans la carte
originale, particulièrement dans la partie centrale et plus profonde du bassin. Du bruit de faible amplitude et
de haute fréquence (courtes longueurs d=ondes) est aussi visible mais on peut facilement le différencier du
signal géologique. Ce bruit est dû à l=utilisation des dérivées premières et verticales dans l=expansion en série
de Taylor ce qui tend à amplifier le bruit présent dans les données.
Reference / Références
Grauch, V. J. S., 1984, TAYLORBA Fortran program using Taylor series expansion for level-surface or
surface-level continuation of potential-field data: U. S. Geological Survey Open-File Report
84-501.
Hobson, G. D. and MacAulay, H. A.,1969, A seismic reconnaissance survey of the Athabasca formation,
Alberta and Saskatchewan, Geological Survey of Canada Paper 69-18, 15 p.
Minty, B. R. S., 1991, Simple micro-levelling for aeromagnetic data (short note): Exploration Geophysics,
22 , no.4, 591-592.
Pilkington, M. and Roest, W.,1992, Draping Aeromagnetic Data in areas of Rugged Topography; Journal
of Applied Geophysics vol. 29; 135-142.
Slimmon, W.L., 2006, Geological Atlas of Saskatchewan; Saskatchewan Industry and Resources,
CD-ROM Version 9.

OF-5676: Local phase of the residual total magnetic field
Descriptive notes
The local phase, or tilt, of the magnetic field as defined by Miller and Sing (1994) is the arctangent of the
ratio of the first vertical derivative of the magnetic field to the magnitude of its horizontal derivative. It is,
therefore, expressed in degrees or radians. The present map is based on micro-levelled residual total
magnetic field data. At high magnetic latitudes, which is the case here, the horizontal derivative achieves a
maximum near or over source edges and tends to zero elsewhere. The vertical derivative is positive over the
source, zero over or near source edges and negative elsewhere. As a result, the tilt tends to be positive over
sources bodies and negative elsewhere. The zero value of the tilt corresponds to the zero contour of the first
vertical derivative. For vertical sided sources at high magnetic latitudes the zero contour corresponds to
magnetic contacts. The main advantage of the use of the tilt is that, being a ratio, anomalies due to both
weak and strongly magnetized sources are given equal weight. Hence, subtle (and often short-wavelength)
anomalies are enhanced making them much easier to trace that in the residual total magnetic field map. The
tilt behaves as an automatic gain control on the magnetic data. The disadvantage is that, since the tilt is
based on a ratio, all the original amplitude information in the magnetic field is lost, so strongly magnetized
sources may produce the same tilt response as weakly magnetized sources.
Tilt angle anomalies within and outside the basin have similar amplitudes. In general their width is larger over
the basin than outside. This is due to a greater depth of the sources of the anomalies. Weak anomalies that
are difficult to follow in the residual total magnetic field map are easier to trace. Good examples are dykes
oriented northwest-southeast cross cutting the central part of the basin.
OF-5676: Phase locale de la composante résiduelle du champ magnétique
Notes explicatives
La phase locale du champ magnétique telle que définie par Miller et Singh (1994) est l=arctangente du
rapport de la dérivée verticale première du champ au module de la sa dérivée horizontale. Elle est donc
exprimée en degrés ou en radians. Cette carte est basée sur les données du champ magnétique total
micro-nivelé. Sous les hautes latitudes magnétiques, ce qui est le cas ici, le module de la dérivée horizontale
est maximum au dessus ou près des arêtes des sources et tend vers zéro ailleurs. La dérivée verticale
première est positive au dessus des sources, zéro au dessus ou près des arêtes et négative ailleurs. La valeur
zéro de la phase locale correspond à l=isovaleur zéro de la dérivée verticale première. Aux hautes latitudes
magnétiques l=isovaleur zéro correspond aux arêtes d=un corps dont les côtés sont sub-verticaux. Le
principal avantage de la phase locale est que puisqu=il s=agit d=un rapport, les anomalies de corps faiblement
ou fortement magnétiques ont un même poids. Donc, les anomalies faibles (et souvent de courte longueur
d=onde) sont rehaussées, ce qui les rend beaucoup plus facile à suivre sur la carte du champ magnétique
total. La phase absolue agit comme un contrôle automatique de gain sur le données magnétiques. Le
désavantage est, que puisque la phase locale est basé sur un rapport, l=information initiale sur l=amplitude du
champ magnétique est perdue et que donc les sources fortement et faiblement magnétique ont des réponses