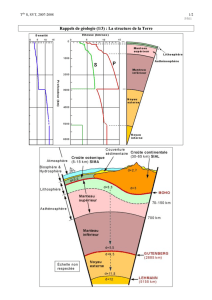
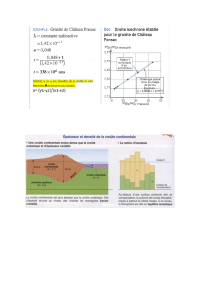
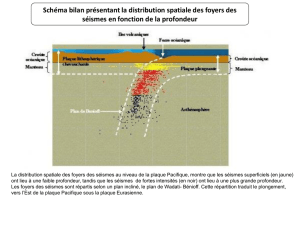
Isostasie – un modèle de relief généralisé On considère

On considère les variations de topographie dans un cas hyper-simple, celui où on change
l’épaisseur de la lithosphère (croûte et/ou manteau) sans rien faire d’autre (pas de
sédimentation, de tranche d’eau, etc.). La figure 1 (dessinée dans le cas d’un amincissement
crustal) montre comment une lithosphère initiale, composée d’une croûte d’épaisseur ec et d’un
manteau lithosphérique d’épaisseur em, s’amincit de sorte que la croûte et le manteau
lithosphérique aient une épaisseur e’c et e’m ; cette lithosphère surplombe une asthénosphère,
dont e’a se trouvent au-dessus du niveau de compensation (choisi à la base de l’ancienne
lithosphère). Cette lithosphère amincie s’élève maintenant à une altitude h au-dessus (ou au-
dessous, si h est négatif) de son altitude d’origine.
On note , et  les densités respectives de la croûte, du manteau lithosphérique et du
manteau asthénosphérique. En général, on a < . Ces différences de densité sont le
moteur des changements topographiques, puisque un amincissement de la croûte implique
qu’on remplace de la croûte (légère) par de l’asthénosphère (plus dense), ce qui contribue à
déprimer la topographie ; un amincissement du manteau au contraire remplace du manteau
lithosphérique dense par de l’asthénosphère plus légère, et donc surélève la topographie. A
l’inverse épaissir la croûte crée du relief, épaissir le manteau lithosphérique crée un trou.
A partir de la figure 1, on peut poser les deux équations suivantes pour rendre compte de la
conservation des épaisseurs, d’une part ; et de l’équilibre des pressions sur le niveau de
référence, d’autre part : 
 (eq. 1)
 (eq. 2)
A ce stade, il est pratique de faire apparaître les facteurs d’amincissement,  et , qui indiquent
l’amincissement respectif de la croûte et du manteau lithosphérique :

On peut alors manipuler ces équations pour arriver à une expression de h en fonction des autres
paramètres : 
 (eq. 3)
Cette équation indique le changement d’altitude lors de variations d’épaisseur de la lithosphère,
en fonction des conditions initiales, des densités et des facteurs d’amincissement de la croûte et
du manteau lithosphérique. De façon générale, on note que le terme « crustal » est négatif, car
 alors que le terme mantellique est positif. De même le contraste de densité entre croûte
et manteau lithosphérique est plus important qu’entre manteau lithosphérique et
asthénosphère, le terme crustal a donc un poids plus important dans l’équation. Enfin, bien que
cette équation ait été établie en considérant un cas d’amincissement, elle marche aussi en
épaississement : dans ce cas , le terme crustal change de signe.
Le tableau 1 donne des valeurs typiques pour les différents paramètres
ec
30 km
em
70 km
2700 kg.m-3
3300 kg.m-3
3250 kg.m-3
Avec ces valeurs, on arrive à peu près à 
 et  , le terme crustal pèse
donc 5 fois plus lourd que le terme mantellique (le contraste de densité est 10 fois plus
important mais l’épaisseur d’origine deux fois moindre, au final on a donc un facteur 5)
On peut alors construire un diagramme dans lequel on va figurer la variation de l’épaisseur de la
croûte en fonction de celle du manteau lithosphérique ; dans ce diagramme on va
« cartographier » la topographie crée.
L’équation 3 fait apparaître  et . Pour (0,0) on a , c’est-à-dire pas de
variation d’épaisseur. En amincissement, donc  (de même pour ). A
l’inverse en épaississement , donc . Si on représente directement les termes de
l’équation, dans un diagramme  vs. , on se retrouve avec l’amincissement dans le
cadrant en haut à droite, et l’épaississement en bas à gauche (ce qui ne semble pas forcément
très intuitif…), on va donc construire le diagramme en inversant les signes, et en représentant
 vs.  pour avoir l’épaississement du côté positif des axes.
Dans ce diagramme, on cherche les lignes d’égale topographie. La ligne d’altitude nulle, h=0, est
telle que 
. Avec les coefficients du tableau 1, c’est une
droite de pente  passant par l’origine. La ligne d’altitude z est une droite de même pente,
coupant l’axe des ordonnées à la valeur z (en kilomètres). On peut donc dessiner l’abaque de la
figure 2 :

Ce diagramme peut être alors utilisé pour discuter de la topographie crée par différents
phénomènes :
On a l’habitude de séparer deux modèles, un rifting « actif » dans lequel un panache mantellique
est responsable d’un amincissement de la lithosphère, et d’un « bombement thermique », qui
précède la formation de failles et l’aminicissement de la croûte ; et un rifting « passif », dans
lequel l’aminicissement de la lithosphère précède la remontée asténosphérique. Ces deux
modèles peuvent se représenter sur l’abaque que l’on vient d’établir (figure 3). Dans ce
diagramme un amincissement de la croûte se traduit par une variation de , et un
amincissement du manteau par une variation de .

- Rifting actif (en vert) : on amincit le manteau lithosphérique sans toucher à la croûte (
diminue,  ne change pas). On évolue vers des altitudes plus importantes : on crée un
« bombement thermique ». Notez que les paramètres choisis ne permettent pas de créer
plus de 1000 m de topographie, même si on supprime tout le manteau lihosphérique et
qu’on ne laisse plus que la croûte : c’est peu comparé à ce que l’on observe en Afrique de
l’Est par exemple, il faudrait un manteau encore plus léger pour provoquer plus de
surrection. Si le manteau qui « remplace » la lithosphère a une densité de 3.2 au lieu de
3.25, la pente des droites iso-altitudes devient 2 :5 au lieu de 1 :5 (figure 4) et on peut
arriver à 2 km de topographie.
- Rifting « passif » (en orange). On amincit à la fois le manteau et la croûte ( et 
diminuent). La flèche orange indique une situation d’aminicissement homogène, où
croûte et manteau lithosphériques sont amincis de la même quantité. Ce n’est pas la
seule possibilité, mais à part dans des cas où on amincissirait énormément le manteau, et
peu la croûte, on évolue de toutes façons vers des altitudes négatives (c’est-à-dire qu’on
crée une dépression). Bien entendu, si par la suite on amincit la lithosphère mantellique
seule (panache asténosphérique induit par l’amincissement, par exemple) on va
augmenter à nouveau les altitudes (surrection post-rifting, comme dans le Massif
Central).

Comme dans le cas précédent, un facteur clef va être l’équilibre entre épaississement de la
croûte et de la lithosphère. On peut étudier trois cas caricaturaux :
- Epaississement de la croûte, mais pas du manteau lithosphérique. C’est pas exemple la
formation d’un prisme orogénique avec décollement au moho. On crée une topographie
importante, de type plateau tibétain par exemple.
- Epaississement mixte, croûte + manteau. C’est une zone de collision avec empilement
d’écailles lithospériques, on double l’épaisseur de la croûte, et de la lithosphère
mantellique. On crée aussi du relief, mais moindre (dans l’exemple, on a un
épaississement homogène). C’est peut-être le cas des Alpes. Dans un cas extrême (si on
épaissit plus le manteau que la croûte) on pourrait former une dépression et pas un
relief.