Chapitre 7 : Grandeurs composées 1.

Chapitre 7 : Grandeurs composées 1.
1. Problème
D'après une tâche complexe élaborée par une équipe de l'Académie Bordeaux
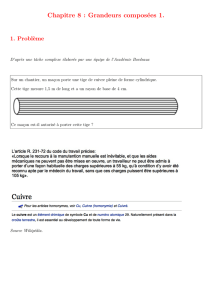
Sur un chantier, un maçon porte une tige de cuivre pleine de forme cylindrique.
Cette tige mesure 1,5 m de long et a un rayon de base de 4 cm.
Ce maçon est-il autorisé à porter cette tige ?
Source Wikipédia.

Masse volumique des éléments à l'état standard, à température et pression ambiantes, en g/cm3.
Formulaire Volume

2. Résolution du problème et synthèse.
•On calcule le volume de la tige :
V = π × 4 × 4 × 150
V = 2400 π
Le volume de la tige est égale à 2400 π cm3
•On calcule la masse de la tige
La masse volumique du cuivre est de 8,96 g.cm-3
Masse (g) 8,96 x
Volume (cm3) 1 2400 π
x = 2400 π × 8,96
x = 21504 π
x ≈ 67 557 par arrondi à l'unité.
La masse de la tige est donc d'environ 67,6 kilogrammes par arrondi au dixième de kilogramme.
Conclusion : L'ouvrier peut porter la tige si le médecin l'autorise à le faire.
La masse d'une substance est proportionnelle au volume qu'elle occupe. Un coecient de
proportionnalité est la masse volumique de la substance.
La masse volumique d'une substance en g.cm-3 est le quotient de la masse de la substance homogène
(en g) par le volume qu'elle occupe (en cm3).
Vocabulaire : On dit que la masse volumique est une grandeur quotient.
Exemple : La vitesse moyenne est une autre grandeur quotient.

3. Conversions d'unité
Exercice
Tout corps qui se déplace possède une énergie cinétique. L'énergie cinétique est la diérence d'énergie
entre un solide au repos et la même solide en mouvement de translation ou de rotation.
L'énergie cinétique que l'on nomme Ec se calcule de la façon suivante :
Ec =
1
2
mv2
•Ec : énergie cinétique en Joule (J).
•m : masse du solide en kg.
•v : vitesse du solide en m.s-1.
L'armation suivante est-elle vraie ?
Armation :
Quelle est l'énergie cinétique d'une voiture d'une tonne roulant à 50 km.h-1 est égale à la moitié de
l'énergie cinétique d'une voiture d'une tonne roulant à 100 km.h-1?

On commence par convertir la masse et la vitesse dans les « bonnes » unités :
•50 km.h-1 = 50 000 m.h-1 =
50000
3600
m.s-1 =
500
36
m.s-1
•1T = 1000 kg
On calcule maintenant l'énergie cinétique de la voiture :
Ec =
1
2×1000×
(
500
36
)
2
Ec ≈ 96 450,6 par arrondi au dixième.
Conclusion : L'énergie cinétique de la voiture est environ égale à 96 451 J par arrondi à l'unité.
En procédant comme dans la question 1, on a montré dans le cahier d'exercices que l'énergie cinétique
de la voiture roulant à 100 km.h-1 était environ égale à 385 803 J par arrondi à l'unité.
Remarque :
La vitesse de la voiture dans le second cas est 2 fois plus grande que dans le premier cas.
Son énergie cinétique quant à elle est 4 fois plus grande.
Cela s'explique par le fait que dans la formule la vitesse soit au carré et 22 = 4.