Les effecteurs 1.Les inhibiteurs

Les effecteurs
Les effecteurs sont des molécules qui ont deux propriétés.
•elles se fixent spécifiquement sur l'enzyme,
•elles ont un effet sur la cinétique de la réaction.
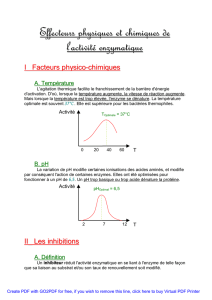
On dit que M1 est un activateur car pour une même concentration en Substrat ([S]), la
vitesse de réaction (Vi) augmente également.
On dit que M2 est un inhibiteur.
Les effecteurs peuvent être activateurs / inhibiteurs.
Il faut que l'effecteur se fixe sur l'enzyme.
L'EDTA complexe le Mg2+ (et Ca2+) du coup la BetaGal a
bcp moins de Mg2+ et la vitesse Vi diminue. Par contre
l'EDTA ne se fixe par sur l'enzyme, ce n'est donc pas un
effecteur.
1. Les inhibiteurs
•Les inhibiteurs irréversibles
Ils sont plutôt des agents dénaturant de l'enzyme.
•Les inhibiteurs réversibles
E + I <=> EI
ki = ([E] . [I]) / [EI]
ki = constante d'inhibition; c'est une
concentration (mol/L).

Inhibition compétitive
Il existe une compétition entre le Substrat et l'inhibiteur pour la fixation sur le site actif.
Par exemple la BetaGalactosidase, elle a des analogues structuraux comme le
thiogalactosidase.
Ex: Succinate Deshydrogénase:
Il existe des analogues structuraux comme: l'oalate, le malonate, le glutarate
Ces trois molécules sont des inhibiteurs, se
fixant sur l'enzyme.

➢Étude cinétique
Comportement d'un inhibiteur compétitif:
- Vm inchangé (ou peu)
- KM augmente
➢Relation Vi = f ( [S] ; [I] )
E + S <=> ES --> E + P
E + I <=> EI
Il n'existe jamais de forme EIS!!
[E]T = [ES] + [E] + [EI]
kM = ([E] . [S])/[ES] et ki = ([E] . [I])/[EI]
ce qui donne:
[E] = (kM . [ES])/[S] et [EI] = ([E] . [I])/ki
si on remplace [E]dans la seconde équation, nous avons:
[EI] = ((kM . [ES])/[S]) . ([I]/ki)
d'où:
[S] . [E]T = (kM . [ES])/[S]) + [ES] . [S] + ((kM . [ES])/[S]) . ([I]/ki)
[S] . [E]T = kM . [ES] + [ES] . [S] + kM . [ES]. ([I]/ki)
factorisons:
[S] . [E]T = [ES] . (kM + [S] + kM . ([I]/ki))
[S] . [E]T = [ES] . (kM . (1 + ([I]/ki)) + [S])
ce qui donne:
[ES] = ([S] . [E]T) / (kM . (1 + ([I]/ki)) + [S])
si on multiplie le tout avec k3, cela donne:
k3 . [ES] = k3 . (([S] . [E]T) / (kM . (1 + ([I]/ki)) + [S]))
d'où:
Vi = (Vm . [S]) / kM . (1 + ([I]/ki)) + [S])
=> Vi = (Vm . [S])/ (kMap +[S])
avec kMap = kM . (1 + ([I]/ki))
Alors inhibition compétitive

Déterminons Ki:
kMap = kM . (1 + ([I]/ki)) uniquement en inhibition compétitive!
Facteur d'inhibition
kMap . ki = kM .([I] + ki)
kMap . ki – kM . ki = kM .[I]
ki = kM – [I] / kMap – kM
D'autre part:
kMap = kM . (1 + ([I]/ki)); or ki = ([E] . [I]) / [EI]
si [I] = ki alors kMap = 2kM
vraie que l'inhibition compétitive!
Inhibition non-compétitive
E +S <=> ES --> E + P
E + I <=> EI
EI + S <=>EIS
ES + I <=> ESI
KM = [E] . [S] / [ES]
ki = [E] . [I] / [EI]
ki' = [ES] . [I] / [ESI]
On doit envisager le cas où il y a deux k
inhibiteurs.
=> inhibition compétitive au sens large!
non productif!
*Cas particulier: ki = ki'
C'est à dire que la fixation du Substrat
sur l'Enzyme n'affecte pas l'affinité de
l'Enzyme pour l'inhibiteur.
=> inhibition non-compétitive
[E]T = [E] + [ES] + [EI] + [EIS]
Vi = ([S] / (kM + [S])) . (Vm / (1 +
([I]/ki)))
où VMap = Vm / (1 + ([i]/ki))
On a donc [I] = ki => VMap = Vm/2
Donc ki est la concentration en
inhibiteur quand Vm diminue d'un
facteur 2.
Ainsi ki varie en fonction de l'inhibition.
Dans ce type d'inhibition VMap diminue car 1/VMap
augmente.
kM reste inchangé (aux erreurs expérimentales
près).
On sait que:
VMap = Vm / (1 + ([i]/ki))
si on multiplie le tout avec ki on a:
VMap = (Vm . ki) / (ki + [I])
C'est à dire
VMap . (ki + [I]) = (Vm . ki)
VMap . ki + VMap . [I] = Vm . Ki
VMap . [I] = Vm . Ki - VMap . ki
VMap . [I] = ki . (Vm - VMap)

D'où:
ki = (VMap . [I]) / (Vm – Vmap)
on rappelle que ki est une
concentration.
Et si ki ki' alors kMap = kM . ((1+
([I]/ki)/1+([I]/ki'))
=> inhibition non-compétitive où
ki'>ki
ici, avec l'inhibiteur Vm diminue et
1/Vm augmente.
Inhibition anti-compétitive (ou in-compétitive)
non productif!
Ici l'inhibiteur ne se fixe pas sur l'enzyme mais sur le complexe [ES].
On a donc :
[E]T = [E] + [ES] + [ESI] ici [EI]
n'existe pas!
Ce qui donne:
Vi = (Vm . [S]) / (KM + [S] . (1+([I]/ki)))
si on divise par (1+([I]/ki)), on a
Vi = ((Vm /(1+([I]/ki))) . [S]) / (KM/(1+
([I]/ki)) + [S])
cad
Vi = (VMap . [S]) / (KMap + [S])
avec VMap = Vm / (1+([I]/ki))
et KMap = KM / (1+([I]/ki))