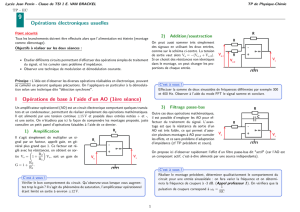
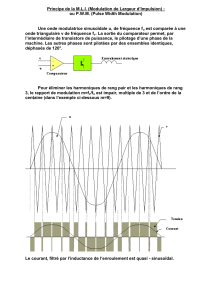
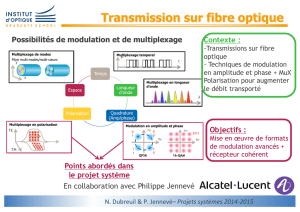
ELEN008-0 Principes des télécommunications analogiques

ELEN008-0
Principes des télécommunications analogiques et
numériques
Institut Montefiore
Service de Télécommunications et d’Imagerie
Professeur Marc Van Droogenbroeck
Février 2013 (version 6.14)

i

Remerciements
Pour rédiger ces notes, j’ai bénéficié du concours de C. Demoulin et de J.-M. Wagner. Que
par ces mots, ils soient remerciés pour leur aide précieuse et pour leur dévouement.
Prof. Marc Van Droogenbroeck
ii

Notations
Cadre analytique :
N N ={0,1,2,...}
Z Z ={... −2,−1,0,1,2,...}
REnsemble des réels
Constantes :
jVecteur unité de l’axe imaginaire j=√−1
kBConstante de Boltzmann =1,38 ×10−23 Joule / degré Kelvin
Variables et fonctions :
tVariable de temps continue
fVariable fréquence
ωVariable de pulsation ω= 2πf
TPériode d’un signal
T0Période fondamentale d’un signal
△xPas d’échantillonnage en x
△yPas d’échantillonnage en y
x(t)Fonction à valeurs continues, définie pour tout temps t
h(t)Réponse impulsionnelle d’un système
H(f)Transmittance d’un système linéaire
f[n]Fonction échantillonnée, fonction discrète
Variables et fonctions de modulation :
m(t)Signal modulant, normalisé à 1:|m(t)| ≤ 1
s(t)Signal modulé
kaTaux de modulation
βIndice de modulation
EbÉnergie par bit
DDébit binaire [b/s]
RRapidité de modulation [baud]
iii

Notations fonctionnelles :
|a|Valeur absolue
−→
aVecteur
kakNorme de a
−→
a .−→ bProduit scalaire de −→
aet −→
b
−→
a×−→ bProduit vectoriel de −→
aet −→
b
∇.−→ aDivergence de −→
a
∇ × −→ aRotationnel de −→
a
∇2ϕLaplacien de ϕ
∇ϕGradient de ϕ
X∗Complexe conjugué de X
Re (a)Partie réelle de a
Im (a)Partie imaginaire de a
X(f)Transformée de Fourier du signal x(t)
⇋Correspondance entre un signal et sa transformée
⊗Convolution
⊕OU exclusif ou addition modulo-2
sin(πx)
πx = sinc (x)Sinus cardinal de x
δ(.)Fonction delta de Dirac
Jn(x)Fonction de Bessel d’ordre n
erfc(.)Fonction erreur complémentaire
Fonctions stochastiques :
p(A)Probabilité de A
aValeur moyenne de a
µXEspérance mathématique du signal X
σ2
XVariance de X
ΓXX (τ)Fonction d’autocorrélation du processus aléatoire stationnaire X(t)
γX(f)Densité spectrale de puissance de X(t)
N0Densité spectrale de puissance de bruit
iv