Monopole 1

Dossier révision oral économie 1/4 Microéconomie – le marché en monopole
DOSSIER PRÉPARATOIRE AUX RÉVISIONS DE L'ÉPREUVE D'ÉCONOMIE - ORAL DE L'ESM
1. MICROECONOMIE
D. LE MARCHÉ EN MONOPOLE
1. L'équilibre d'un marché en monopole non discriminant
a. Exercice « modèle »
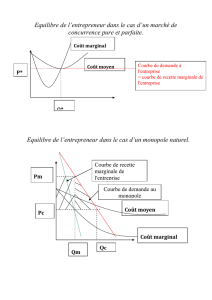
Soit un marché en situation de monopole. La fonction de demande prend la forme suivante:
Qd = 2000 - 100P Le monopole a une fonction de coût de la forme: CT = 4000 + 0,01Q²
1. Calculer le coût moyen et le coût marginal.
2. Calculer les différentes recettes du monopole.
3. Calculer l’équilibre de ce marché (prix d’équilibre, quantité échangée et profit du monopole)
4. Quelle aurait été le résultat en CPP ?
Réponse:
1. - Le coût moyen est le coût unitaire. Il nous est donné par le rapport entre le coût total et les quantités produites :
CM(Q) = CT(Q)/Q donc CM(Q) = 4000/Q + 0,01Q
- Le coût marginal est la variation du coût total provoquée par la production d’une unité supplémentaire. On exprime
l’équation du coût marginal en dérivant la fonction de coût total par rapport à la variable Q.
Cm (Q) = dCT(Q)/dQ = 0,02Q
2. Pour une firme en monopole le prix n’est plus une donnée mais une variable qu’elle fixe et qu’elle va devoir diminuer
pour augmenter les quantités vendues (loi de la demande).
- La recette totale nous est donnée par l’équation : RT(Q) = P(Q) x Q
Pour exprimer la fonction P(Q) (qui est la fonction de prix : elle nous indique quel doit être le prix pour chaque quantité
vendue), on inverse la fonction de demande : P(Q) = 20 – Q/100
La fonction de recette totale est donc : RT(Q) = 20Q – Q²/10
- La recette moyenne nous indique la recette unitaire, donc pour chaque unité vendue. On l’exprime en faisant le rapport
entre la RT et les quantités produites : RM(Q) = RT(Q)/Q
Donc : RM(Q) = 20 - Q/100. La RM(Q) est donc confondue avec la fonction de prix.
- La recette marginale nous indique quelle est la variation de la recette totale lorsque la firme augmente sa production d’une
unité. On l’exprime en dérivant la fonction de recette totale par rapport à la variable Q : Rm (Q) = dRT(Q)/dQ = 20 - Q/50
3. - Une entreprise, quelle que soit la structure du marché, a pour objectif de maximiser son profit. Pour cela, elle fait un
raisonnement à la marge : pour chaque unité de bien qu’elle peut produire, elle compare ce que lui rapporte cette unité
(Rm) et ce qu’elle lui coûte (Cm). Tant que le Cm<Rm, elle offre cette quantité. Mais le Cm est croissant alors que la Rm est
décroissante ; donc les deux fonctions finissent par se croiser. La quantité pour laquelle le Cm=Rm est donc celle qui
maximise le profit de la firme.
- Raisonnement mathématique : on cherche à maximiser la fonction de profit (Pro) : Pro(Q) = RT(Q) – CT(Q) lorsque l’on
recherche le maximum (optimum) de cette fonction, on égalise la dérivé première à zéro : (Pro(Q))’ = Rm(Q) – Cm(Q) = 0
donc le profit est maximum lorsque Rm(Q) = Cm(Q)
- Résolution : 0,02 Q = 20 - Q/50  Q = 1000 - Q  Q = 500
Pour connaître le prix de vente, on remplace Q par sa valeur dans la fonction de prix :
P(Q=500) = 20-500/100 = 15
A ce niveau: Pro = PQ - CT = 15x500 - 4000 - 0,01(500)² = 1000  Pro = 1000
4. En CPP, l’équilibre sur le marché se fait au point de rencontre entre l’offre et la demande, donc au point où le Cm(Q) =
RM(Q) : 20 - Q/100 = 0,02 Q  Q = 666,67 alors P = 13,33 et Pro = 444,41

Dossier révision oral économie 2/4 Microéconomie – le marché en monopole
b. Exercice d'entraînement
Une firme fabrique un bien, X, qu'elle est seule à produire. La demande de ce produit a pour fonction : DX = -3P + 450 où P
représente le prix de X. La fonction de coût total de cette firme s'écrit : CT = (X²/4) + 10X + 10. La firme souhaite maximiser
son profit.
a/ Quelles quantités de X produira-t-elle ? [Q=120] A quel prix vendra-t-elle le bien X [P=110]? Quel sera le montant
de son profit ? [8390]
b/ Les résultats seraient ils différents si le marché était en concurrence pure et parfaite ? [Q = 168; P = 94 et  = 7046]
c . Exercice d'entraînement
Une entreprise en situation de monopole a une fonction de coût total de la forme : CT = 0,05q²+90. La fonction de demande
s’écrit : qd = 80-5p.
a. Déterminez le volume produit par cette entreprise, le prix de vente et le profit si l’entreprise cherche à maximiser son
profit. [q=32 ; p =9,6 et P=166]
b. L’état impose à cette entreprise une tarification au coût marginal. Déterminer le volume produit, le prix de vente et le
profit réalisé. [q= 53,33 ; p=5,33 ; P=52,04]
c. Comparez et commentez les situations b et c.
d. Exercice d'entraînement
Une entreprise en situation de monopole est caractérisée par la fonction de coût suivante: CT = (1/4)q² + 15q et écoule sa
production sur un marché où la demande prend la forme: Qd = 30 – (½)p
− Déterminer le couple prix-quantité qui permet à l'entreprise de maximiser son profit. [Q=10; P=40; Pro = 225]
− Quelle est la valeur du surplus social ? comparer avec celui que l'on aurait obtenu en CPP. [mono: SC=100; SP=225;
CPP: SC=324; SP= 81]
d. Exercice d'entraînement
Une entreprise en situation de concurrence pure et parfaite produit un bien X. Le coût total de cette entreprise s'écrit :
CT (X) = 5X3 - 20X² + 45X.
a) Montrez que le coût marginal coupe le coût moyen en son minimum. Expliquez. Illustrez par un graphique.
b) Le prix de vente sur le marché est égal à 50. Déterminez les quantités vendues par l'entreprise ainsi que son profit.
Représentez ce profit sur votre graphique. [Q=2,79]
c) Comment évoluera le marché à long terme ? La demande du bien X est telle que: D (X) = 10 0,1 P. Pouvez-vous en
déduire la production totale du bien X ainsi que le nombre d'entreprises présentes sur le marché. La situation est elle stable
? [Qd = 7,5 alors N = 3,75]
d) On suppose maintenant que cette même entreprise est en situation de monopole et que la demande du bien X ne
change pas. Quelle sera la production de l'entreprise, à quel prix vendra-t-elle ? Calculez son profit. [Q = 2,69 ; P = 73,06 et
pro = 122,88]
0
Quantités produites
Prix fixé par le monopole
500
15
Cm
CM
666
13

Dossier révision oral économie 3/4 Microéconomie – le marché en monopole
2. L'équilibre d'un marché en monopole discriminant
a. Exercice « modèle »
Sur son territoire, une entreprise détient le monopole de la production d’un bien Q pour lequel la demande est de la forme :
Q = -P/5 + 24
1. Le produit n’a pas de substitut, l’entreprise cherche à maximiser son profit. Calculer la quantité produite, le prix
de vente et le profit, la fonction de coût étant : CT = 5/3Q². Faite une représentation graphique de cet équilibre.
2. Sur un territoire voisin, la demande pour le même type de bien est de la forme : Qe = -P/5 + 16. Si l’entreprise
ne satisfaisait que cette demande là, quelle serait sa production, son prix de vente et son profit (la fonction de coût restant
la même) ? Faite une représentation graphique de cet équilibre.
3. L’entreprise décide de satisfaire la demande des deux territoires. Ainsi, à la demande nationale s’ajoute la
demande étrangère. Déterminer la nouvelle quantité produite, le nouveau prix et le nouveau montant du profit. Faite une
représentation graphique de cet équilibre.
4. L’entreprise décide de pratiquer une politique de discrimination tarifaire ; de combien va-t-elle augmenter ses
profits ? Faite une représentation graphique de cet équilibre.
Réponses :
1. La méthode à suivre pour répondre à cette 1ère question est la même que celle que nous avons appliqué dans les
exercices précédents. Je ne vous indique donc que les résultats:
− les fonctions : Cm(Q) = 10/3Q ; RM(Q) = -5Q + 120 ; RT(Q) = -5Q² + 120Q et Rm(Q) = -10Q + 120
− équilibre: Q = 9 ; P = 75; profit = 540
2. La méthode à suivre pour répondre à cette 1ère question est la même que celle que nous avons appliqué dans les
exercices précédents. Je ne vous indique donc que les résultats:
− les fonctions: RM(Q) = -5Q + 80; RT(Q) = -5Q² + 80Q; Rm(Q) = -10Q + 80
− équilibre: Q = 6 ; P = 50 et profit= 240
3. Pour exprimer la fonction de demande totale nous devons additionner les deux fonctions de demande nationale Qt(P) =
Q(P) + Qe(P) = -2/5P + 40 ; On en déduit la fonction de recette moyenne: RMt(Q)= -5/2Q + 100; RTt(Q) = -5/2Q² + 100Q et
Rmt = -5Q + 100
− l'équilibre est déterminé par la rencontre entre le Cm(Q) et la Rmt(Q): -5Q + 100 = 10/3Q
− si l'entreprise ne pratique pas de discrimination tarifaire, elle offria une quantité totale de 12.
− A l'aide de Rmt(Q), on peut déduire le prix qu'elle affichera pour écouler cette quantité: P= 70 ; le profit sera alors de 600.
4. Si l’entreprise pratique une politique de discrimination tarifaire, elle produira une quantité totale de 12, mais elle en
écoulera une part sur le marché national et l'autre part sur le marché étranger. Sur chacun des marchés elle devra égaliser
la Rm (du marché) avec le coût marginal occasionné par la production de 12 unités.
− Cm(Q=12) = (10/3)x12 = 40
− Sur le marché national : Rm = -10Q + 120 = Cm = 40 donc Q = 8 ; puis, à l'aide de la fonction de prix du marché national
(que l'on obtiens en inversant la fonction de demande nationale), on calcule le prix qui sera pratiqué sur ce marché: P =
80
− Sur le marché étranger : RM = P = -5Q + 80 donc RT = -5Q² +80Q et Rm = -10Q + 80. Donc Rm = Cm : -10Q + 80 = 40
→ Q = 4 ; P = 60
b. Exercice « modèle »
Nous reprenons les données de l'exercice donné précédemment (1;d): Une entreprise en situation de monopole est
caractérisée par la fonction de coût suivante: CT = (1/4)q² + 15q et écoule sa production sur un marché où la demande
prend la forme: Qd = 30 – (½)p
a. Quelles seront les conséquences d'une discrimination parfaite du premier degré ? Évaluer les conséquences
économiques de cette décision.
b. Nous postulons qu'il n'applique pas la méthode précédente. Une étude d'un marché étranger lui permet d'affirmer qu'il
serait en situation de monopole dessus et que la fonction de demande prend la forme: Qe = 30 – pe.
Déterminer les prix et les quantités si l'entreprise pratique une discrimination tarifaire sur les deux marchés.
Réponses:
a. S'il pratique une discrimination parfaite, il fera payer le prix maximum à chaque consommateur. Le dernier prix sera celui
pour lequel la Rm = Cm. La Rm étant confondu avec la RM alors nous avons vu précédemment que l'équilibre a lieu au
point: p = 24 et q = 18.
- Le surplus global correspondra au profit du producteur; or, ici j'ai plusieurs prix. Je vais donc chercher le niveau du profit
en faisant la différence entre la RT et le CT:
- Le CT nous est donné par la fonction de coût total: CT = 351
- La RT est (24.18) + (60-24).18.1/2 = 756
Le surplus est donc égal à = 756 – 351 = 405, c'est-à-dire celui que l'on avait en CPP.
b. Pour pratiquer la discrimination tarifaire, il doit rechercher quelle est la quantité à produire au total et le Cm
correspondant. Qt = Qn + Qe = 60-1,5p → P = -q/1,5 + 40 = RM → RT = -q²/1,5 + 40q → Rm = -2q/1,5 + 40
Cm = Rm → q= 13,63 et Cm = 21,81 Nous savons donc qu'il devra au total produire 13,63 unités du bien. Sur chaque

Dossier révision oral économie 4/4 Microéconomie – le marché en monopole
marché, le Cm (21,81) devra être égal avec la Rm du marché:
Marché étranger: Qe = 30-pe → Pe = -q +30 → Rm = -2q +30 Donc –2q+30 = 21,81 → q =4,095 au prix pe = 25,905
Marché national: Q=30-1/2p → Rm = -4q+60 → q = 9,5475 au prix p = 40,905
Calcul du profit : - sans discrimination : Q=13,63 et P = 30,91 alors pro = 170,46
- Avec discrimination : pro = 106,08+390,54-250,89=245,73
c. Exercice d'entraînement
Un monopoleur produit et vend des boomerangs sur deux marchés différents : un marché de compétition (marché 1) et un
marché de jeux de plein air (marché 2). Son coût de production est identique qu’il produise pour l’un ou l’autre marché. Il
est donné par l’équation : CT(Q)=500+40Q où Q est la production totale. Les demandes sur chacun des marchés sont les
suivantes :
P1 = 200 – Q1
P2 = 190 – 3Q2
1. Quel est la quantité vendue et le prix pratiqué lorsque le monopoleur ne différencie pas les deux marchés. Quel profit
réalise-t-il ? [cm = 40; Q = 105; P = 118.75 et profit = 7768,75]
2. Quels sont les quantités vendues et les prix pratiqués lorsque le monopoleur différencie les deux marchés. Quel profit
réalise-t-il ? [Q1= 80 ; q2=25; P1 = 120; P2=115; profit = 7775]
d. Exercice d'entraînement
Soit une entreprise en situation de monopole sur le marché d’un bien. Elle a estimé que la demande qui lui était adressée
provenait de deux types de consommateurs différents. Ces fonctions de demande sont respectivement :
D1(Q) = 65 – 0,5P et D2(Q) = 100 – 1,5P
La fonction de coût total du monopole est donnée par l’équation : CT (Q)= 0,75Q² + 500
1/ Le monopoleur estime que les deux marchés ne sont pas suffisamment cloisonnés. Comment va-t-il se comporter ?
Déterminez la quantité offerte qui maximisera son profit. Quel sera ce profit ? [Q = 33, P = 66, Cm= 49,5 et Pro = 861,25]
2/ Quelle stratégie va-t-il adopter s’il considère que les deux marchés sont étanches ? Quelle est la quantité qu’il produira ?
Comment répartira-t-il ce volume de production ? A combien s’élève son profit à l’optimum ? [Q1 = 20,125 ; P1 = 89,75
Q2 = 12,875 ; P2 = 58,08; Pro = 1237,3]
3/ Calculez les élasticités prix des demandes sur chaque marché. Commentez. [Au point Q1 : e1 = -0,5.89,75/20,125 =
-2,223; Au point Q2 = e2 = -6,767]