Interaction atomes

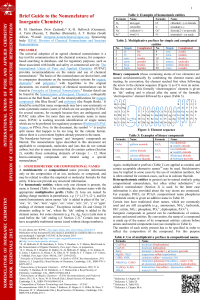
Interaction atomes-lasers
Continuous Regime (Westbrook) 6 cours (in 5 lectures)
1. Simple Models (sans mé canique quantique)
2. Review of some quantum mechanics, density matrix
3. Description of dissipation using the density matrix
4. Applications for 2 level atoms, radiative forces on atoms
5. Bloch Equations for a 3 level atom, application to slow light
6. Analysis of a 3 level atom using an effective Hamiltonian
Pulsed regime (LeGouët) 6 cours or Advanced topics (Bouyer)
http://www.atomoptic.fr/~westbrookc
Bibliography
1. C. Cohen-Tannoudji, B. Diu, F. Laloe, "Mé canique Quantique"
2. G. Grynberg, A. Aspect, C. Fabre, "Introduction aux lasers et à l'optique quantique"
3. E. Rosencher, B. Vinter, "Optoé lectronique"
4. R. Loudon "The quantum theory of light" 3rd Ed.
5. B. Cagnac, J.-P. Faroux "Lasers : Interaction lumiè re-atomes"
6. C. Cohen-Tannoudji, Jacques Dupont-Roc, G. Grynberg, "Processus d'interaction entre atomes et photons"
1. Simple Models
A. The Lorentz Atom (“harmonically bound electron”, "l'é lectron é lastiquement lié ")
refé rence: Grynberg, Aspect, Fabre, "Introduction au lasers et l'optique quantique". p. 367
Begin with a very simple, classical model in which we imagine an electron attached to a fixed point (the nucleus) by a spring.
We approximate the electron + nucleus as a dipole. When the electron oscillates, the dipole radiates energy according to the
Larmor formula (valid if the wavelength of the radiation is much larger than the electron - nucleus separation):
dU
dt
..
..
q2
=
4 ΠΕ0
2 z2
3 c3
2 2
2 e z
3 c3
=
This radiation results in a damping of the electron’
s motion, giving a differential equation for the electron position:
¨
q
1
z + G z + Ω0 2 z =
IE0 e-i Ω t + ccM
m 2
with G =
e2
Ω0 2 3 .
3
mc
2
Calculate G for a hydrogen atom (Λ = 122 nm).
Steady state solution of the differential equation:
zHtL =
1
HzΩ e-i Ω t + ccL,
2
zΩ =
q
m
E0
1
Ω0 2 -Ω2 -i ΩG
.
To find the polarisation P in a gas of such atoms with density Ρ:
PHtL = Ρ dHtL = Ρ q zHtL
PΩ = Ρ q zΩ = ΧHΩL EΩ , Χ = Χ ' + i Χ ''
The second equation defines the electric susceptibility. The index of refraction is : n =
Χ=
Ρ q2
1 + Χ . We find:
Ω0 2 -Ω2 +i ΩG
m Ε0 IΩ2 -Ω0 2 M2 +Ω2 G2
close to resonance H Ω0 - Ω ` Ω0 + ΩL we have:
Χ' =
Χ '' =
Ρ q2
2 m Ε0 Ω0
Ρ q2
2 m Ε0 Ω0
Ω0 -Ω
HΩ-Ω0 L2 +
G2
4
G
2
HΩ-Ω0 L2 +
G2
4
Calculate the index of a gas of helium atoms (Λ = 58 nm) at atmospheric pressure IΡ = 2.5 ´ 1025 m-3 M.
2
12LM-1.nb
12
-D
In[1]:=
PlotB:
,
2
D +14
>, 8D, - 5, 5<F
2
D +14
2.0
1.5
1.0
Out[1]=
0.5
-4
2
-2
4
-0.5
-1.0
Here G = 1 et D = Ω - Ω0 .
B. Einstein’
s model of the atom
ref. Loudon, The quantum theory of light, ch. 1, Kleppner, Physics Today, Feb 2005, p. 30
Two level atoms f, e, in a bath of thermal radiation with spectral and volume density u(Ω). Einstein supposed the existence of:
absorption with rate: B f ®e uHΩL
stimulated emission with rate: Be® f uHΩL
spontaneous emission with rate: A
In other words we have "Rate equations" for the populations:
Π f = I-B f ®e uHΩL Π f + Be® f uHΩL Πe M + A Πe
Πe = -Π f .
Using the Boltzmann law:
uHΩL =
ÑΩ3
1
Π2 c3 eÑِk T -1
Πe
Πf
= e-ÑΩ0 k T , and setting Be® f =B f ®e = B, A  B =
ÑΩ0 3
Π2 c3
, one can recover Planck’s formula:
.
Two interpretations:
If you accept Planck Þ stimulated and spontaneous emission must exist.
If you accept Einstein’s hypotheses Þ a demonstration of the Planck radiation law.
Applications d'Einstein
1. Saturation
These ideas can also be used out of equilibrium. Let u = u0 in a narrow range of frequencies DΩ around Ω0 . The steady state solution for
the populations is:
HB u0 + AL Πe = B u0 Π f Þ Πe =
B u0
2 B u0 + A
Atom cease to absorb if u0 is large.
2. Absorption, gain
Suppose u = uHzL, with the same spectrum as in 1. What is the transmitted light intensity through a vapor cell of density Ρ? For u small, one
finds an attenuation coefficient trouve une attenuation exponentielle avec coefficient d'absorption Ρ
possibles.
Comparison of the models:
1. Lorentz
Input: Ω0 , q, m
Basic physical quantities: d = q z, E
dP
Output: G,
, Χ, lineshape ...
dW
2. Einstein
Input: Ω0 , A, B
Basic physical quantities: Π f , Πe , uHΩL
Output: Planck’s formula, absorption, gain, saturation ...
Can we put these together? Where is the Schroedinger equation?
BÑΩ
c DΩ
. Mais autres situations sont
Basic physical quantities: d = q z, E
dP
Output: G,
, Χ, lineshape ...
dW
2. Einstein
Input: Ω0 , A, B
Basic physical quantities: Π f , Πe , uHΩL
Output: Planck’s formula, absorption, gain, saturation ...
Can we put these together? Where is the Schroedinger equation?
12LM-1.nb
3