énoncé

Spé ψ
ψψ
ψ 2011-2012 page 1/5 Devoir n°4
Spé ψ
ψψ
ψ 2011-2012 Devoir n°4
MÉCANIQUE DES FLUIDES
P ARTIE I
R ESULTANTE DES FORCES S ’ EXERÇANT SUR UNE SPHERE
On s’intéresse à l’écoulement d’un fluide incompressible de viscosité η et de masse volumi-
que ρ autour d’une sphère de centre O de rayon R à très faible nombre de Reynolds (R
E
<< 1). On
rappelle que le nombre de Reynolds est
E
/
R R v
= ρ η
où v est la vitesse de la sphère, ρ la masse
volumique du fluide et η la viscosité. Dans ce problème, la pesanteur est négligée. On note
(
)
, ,
x y z
e e e
la base associée au repère ( O, x, y, z ) .
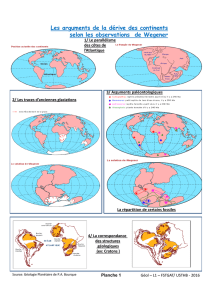
L’angle θ est l’angle entre OM et
z
e
et l’angle ϕ est l’angle entre Om et
x
e
, vecteur unitaire
de l’axe Ox, m étant le projeté orthogonal de M dans le plan (O, x, y).
À une distance z très grande devant R , la pression est notée p ∞ , l’écoulement est uniforme et
la vitesse v ∞ est parallèle à l’axe Oz :
z
v v e
∞∞
= . Cet écoulement permanent est caractérisé dans un
repère sphérique par un champ de vitesse
(
)
, ,
v v r
= θ ϕ
et un champ de pression
(
)
, ,
p p r
= θ ϕ
qui
vérifient l’équation de Navier-Stokes,
( )
grad
Dv
p v
Dt
ρ = − + η ∆
.
On rappelle que
(
)
(
)
(
)
(
)
rot rot grad div
A A A
= − ∆
;
(
)
(
)
div rot 0
A
=
;
( )
(
)
div grad
f f
= ∆
.
I-1-a) Quelle est l’unité du nombre de Reynolds RE dans le Système International ? On justi-
fiera par une analyse dimensionnelle.
b) Rappeler dans le cas général, l’équation locale de conservation de la matière. Que
devient cette relation dans le cas d’un fluide incompressible ?
(
)
, ,
M r
θ ϕ
figure 1
ligne de champ de vitesse
z
x
y
ϕ
θ
m
v
∞
plan perpendiculaire à
Oz

Spé ψ
ψψ
ψ 2011-2012 page 2/5 Devoir n°4
I-2-a) En comparant les différents termes de l’équation de Navier-Stokes, montrer que cette
dernière peut approximativement s’écrire
( )
grad
p v
= η ∆
. Quelle en est la conséquence sur la ré-
versibilité ou l’irréversibilité de l’écoulement ?
b) En déduire que le laplacien de p vérifie
0
p
∆ =
.
c) Justifier que la pression p est indépendante de la variable ϕ et préciser la direction
de la résultante des forces pressantes
P
F
sur la sphère.
d) Vérifier que
(
)
2
cos
3
2
v R
p p
r
∞
∞
η θ
= − est solution du problème.
On rappelle qu’en coordonnées sphériques, pour une fonction f indépendante de ϕ, on a
(
)
( ) ( )
(
)
2
2 2
, ,
1 1 sin
sin
f r f r
f r
r r r r
∂ θ ∂ θ
∂ ∂
∆ = + θ
∂ ∂ θ ∂θ ∂θ
e) En déduire la résultante des forces pressantes
P
F
. L’élément de surface sur une
sphère de rayon R est
(
)
2
sin
dS R d d
= θ θ ϕ
.
f) Sachant que la résultante des forces visqueuses vaut 4
F Rv
η
∞
= πη , en déduire la
force totale subie par la sphère.
I-3) Considérons maintenant une sphère de vitesse v , de rayon R en mouvement uniforme
dans un fluide de viscosité η et de masse volumique ρ .
a) On cherche à déterminer la traînée exercée sur la sphère. Cette force exercée par le
fluide sur la sphère est fonction de v , R , ρ et R
E
. La force de traînée peut se mettre sous la forme :
( )
E
2
x
F C R R v
α γ λ
π
= ρ
où
(
)
E
x
C R
représente une fonction de R
E
et α , γ et λ sont des entiers natu-
rels. Par une analyse dimensionnelle, déterminer les nombres α, γ et λ.
b) Dans le cas d’un écoulement rampant, (R
E
< 1) , nous obtenons la loi dite de Sto-
kes : 6
F R v
= − π η
. Préciser alors la valeur de C x en fonction de R
E
.
c) Que devient cette force pour un fluide parfait ?
I-4) Dans le cas des écoulements à grand nombre de Reynolds, la force de traînée
T
qui agit
sur la sphère est proportionnelle au coefficient de traînée C, sans dimension, et au carrée de la vi-
tesse selon la relation
2
1
2 4
D
T C U U
π
= − ρ  .
a) Évaluer la valeur numérique du nombre de Reynolds dans le cas d’un ballon de
football se déplaçant dans l’air avec une vitesse de 100 km⋅h
–1
. Que peut-on en déduire ?
On utilisera les valeurs numériques suivantes :
Masse volumique de l’air ρ =1 , 2 kg⋅m
–3
; Viscosité cinématique de l’air η = 16 , ×10
–5
Pa⋅⋅s ;
Module de l’accélération de la pesanteur g = 9 , 8 m⋅s
–
2
;
Masse du ballon m = 0 , 50 kg ; Diamètre du ballon D = 22 cm.
L’axe Oz qui oriente les grandeurs vectorielles est dirigé selon la verticale descendante, son
vecteur unitaire est noté
z
e
. On cherche à valider expérimentalement la loi donnant la force de traî-
née en mesurant la vitesse d’un ballon soumis au seul champ de pesanteur. Ce dernier est lâché
d’une hauteur de 27 m dans une enceinte contenant de l’air au repos, avec une vitesse initiale
00
z
v v e
= telle que v
0
> 0. On procède à des séries de mesures du module de la vitesse instantanée
au cours du mouvement par vélocimétrie laser. L’intervalle τ = 30 ms séparant deux mesures suc-
cessives est constant.

Spé ψ
ψψ
ψ 2011-2012 page 3/5 Devoir n°4
On donne dans le tableau ci-dessous un extrait des valeurs v
i
du module de la vitesse, mesu-
rées aux dates t
i
= i × τ .
i1234567891011
v
i
(m⋅s
–1
)5,220 5,480 5,736 5,988 6,237 6,482 6,726 6,986 7,253 7,522 7,789
b) Évaluer le module de l’accélération instantanée a
i
à la date t
i
en fonction de v
i+1
, v
i
et τ .
c) En utilisant le théorème de la résultante cinétique, établir la relation scalaire entre
les grandeurs m, a
i
, g et la norme T
i
de la force de traînée à la date t
i
.
d) Reproduire et compléter le tableau ci-contre. À partir de ces données, représenter
les points de coordonnée
2
,
i i
v T
et
(
)
10 E
log ,
R C
. Commenter les diagrammes obtenus.
i1 2 3 4 5 6 7 8 9 10
vi2 (m2 ⋅ s–2)
Ti (N)
C
log10(RE)
Partie II
R ESULTANTE DES FORCES S ’ EXERÇANT SUR UNE PLANCHE
Le skimboard est un sport qui se pratique au bord de la plage. Cette partie s’intéresse à une
pratique nommée « flat ». À marée basse, l’eau qui se retire lentement laisse des étendues où seule
subsiste une mince couche d’eau. Le sportif lance une planche devant lui, court et monte dessus : il
peut ainsi glisser sur plusieurs mètres. La planche est légèrement inclinée : l’avant pointant vers le
haut. Messieurs Tuck et Dixon de l’Université d’Adélaïde (Australie) ont proposé le modèle suivant
pour rendre compte du mouvement de la planche.
Le référentiel lié à la plage est supposé galiléen. L’eau est assimilée à un fluide parfait in-
compressible de masse volumique ρ . Elle est surmontée par de l’air à la pression p0 ou par la plan-
che. L’écoulement de l’eau est supposé plan. L’influence de la gravité est négligée dans l’étude de
l’écoulement. La planche, supposée rectangulaire de largeur L, se déplace à la vitesse
x
V V e
− = −
constante par rapport au référentiel lié à la plage et fait un angle α avec l’horizontale (dit angle
d’attaque) supposé petit dans tout le problème. Loin de la planche, l’eau est supposée au repos dans
le référentiel lié à la plage.
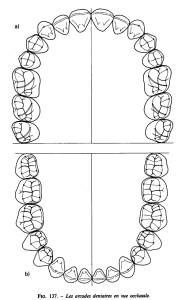
La figure 2 représente quelques paramètres du problème dans le référentiel R lié à la plan-
che. Le mouvement de la planche provoque un jet d’eau d’épaisseur δ qui se détache de l’avant de
la planche.
Au-dessus de la ligne de courant en pointillé, l’eau constitue le jet. En dessous, l’eau
s’écoule vers l’arrière de la planche. Loin à l’avant de la planche, la hauteur d’eau est hT +
δ tandis
Figure 2 : Modélisation de l’écoulement dans le référentiel lié à la planche
V
p
0
δ
h
A
h
T
x
T
x
A
h
T
x
z
α
m
ℓ
V
V
−

Spé ψ
ψψ
ψ 2011-2012 page 4/5 Devoir n°4
qu’elle vaut hT derrière. La surface de la planche qui n’est pas en contact avec le jet est dite « sur-
face mouillée ». Elle est de longueur
m
ℓ
. La hauteur d’eau hA désigne la hauteur du point de sta-
gnation (défini comme l’intersection de la planche et de la ligne de courant en pointillé).
On notera
( )
P
Σ
R
la quantité de mouvement d’un système Σ par rapport au référentiel R et
on définit
( ) ( )
x
x
P P e
Σ = Σ ⋅
R
.
Sauf indication contraire, l’étude sera menée dans le référentiel R lié à la planche où
l’écoulement est stationnaire.
Dans cette sous-partie on travaillera dans la région située sous la surface mouillée
[
]
(
)
A T
,
x x x
∈. On suppose que la hauteur d’eau h , la pression dans l’eau p et le champ des vitesses
dans l’eau
v
ne dépendent que de l’abscisse x du point de l’écoulement considéré. Le champ des
vitesses est a priori bidimensionnel mais en de nombreux points de l’écoulement la composante
verticale de la vitesse est négligeable devant la composante horizontale ainsi
(
)
x
v v x e
∼ . On note
(
)
A A
x
v x v e
= où x
A
est l’abscisse du point de stagnation.
II-1) Résultats préliminaires
a) En faisant un bilan de masse sur un système que vous expliciterez, montrer la re-
lation
(
)
(
)
T
h V h x v x
=.
b) Rappeler l’équation locale de conservation de la masse. À quelle relation entre V
et v ( x ) mène-t-elle ? Cette relation est en contradiction avec la relation précédente : lever le para-
doxe.
c) Dans le cadre de ce modèle, l’écoulement est-il rotationnel ? On justifiera.
d) Rappeler l’énoncé du théorème de Bernoulli approprié à ce modèle et le démon-
trer.
II-2) Calcul direct
a) Soit x désignant l’abscisse d’un point situé sur la surface mouillée de la planche,
montrer que :
( ) ( )
2
2T
02
11
2
h
p x p V
h x
− = ρ −
.
b) Établir une expression de h ( x ) en fonction de α, h
T
, x et x
T
.
c) On suppose que la pression de l’eau au contact de la surface non mouillée de la
planche est p
0. La résultante totale des forces de pression
F
que les fluides exercent sur la planche
possède deux composantes :
x z
x z
F F e F e
= + . On cherche leurs expressions approchées dans le ca-
dre des faibles valeurs de l’angle α. Montrer que
( )
2
m
1
2
z
V
F L
ρ
= − λ
ℓ où l’on donnera l’expression
de λ en fonction de h
T
et h
A. Établir l’expression de
F x .
d) Soit T un point situé à l’arrière de la planche. Justifier précisément que le moment
des forces de pression M par rapport à l’axe
(
)
,
y
T e
est
( ) ( )
T
2
T
T2
1
A
x
x
h
K x x dx
h x
= − −
∫
M où l’on
exprimera K en fonction de données de l’énoncé. On ne demande pas de calculer cette intégrale.
e) Un calcul, que l’on ne demande pas de mener, permet d’établir que
( )
22
m
4
VL f ρ
= λ
M ℓ où
(
)
f
λ
est une fonction de λ. Exprimer, en fonction de
m
ℓ
, f et λ, la dis-

Spé ψ
ψψ
ψ 2011-2012 page 5/5 Devoir n°4
tance
p
ℓ
de l’axe
(
)
,
y
T e
à laquelle doit se placer le sportif pour qu’il puisse être à l’équilibre dans
R (on supposera que la planche possède une masse négligeable devant celle du sportif). On admet-
tra que
p m
<
ℓ ℓ
.
II-3) Calcul par un bilan de quantité de mouvement
On se propose, par un bilan de quantité de mouvement, de retrouver la résultante des forces
de pression s’exerçant sur la planche.
a) En choisissant comme système fermé Σ, l’eau contenue dans le volume situé sous
la planche entre les abscisses x
A
et x
T
(zone hachurée sur la figure 3) et celle qui va pénétrer dans ce
volume entre les dates t et t + dt , trouver une relation liant
(
)
x
dP
dt
Σ
R
, ρ, L , h
T, λ et
V .
b) On note p
A
la pression en x = x
A
:
(
)
A A
p p x
=. Montrer que la composante selon
l’axe x de la résultante des forces s’exerçant sur Σ peut s’écrire
(
)
A 0 A
x
p p h L F
− −
.
c) Retrouver l’expression de F
x établie à la question II-2-c.
II-4) On se propose dans cette question de montrer la nécessité de l’existence du jet d’eau
pour assurer la consistance du modèle.
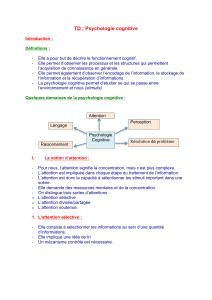
a) En choisissant, comme système fermé Σ, l’eau contenue dans le volume hachuré
figure 4 et celle qui va pénétrer dans ce volume entre les dates t et t + dt , trouver une relation liant
(
)
x
dP
dt
Σ
R
, ρ, L , δ et V .
b) En déduire une relation liant F
x, ρ,
L , δ, α et V . Conclure.
figure 3
V
p
0
δ
h
A
h
T
x
T
x
A
h
T
x
z
α
m
ℓ
V
V
−
V
V
−
p
0
δ
h
A
h
T
x
T
x
A
h
T
x
z
α
m
ℓ
Figure 4
V