Introduction - Nathalie Rion

Montage n° 15 - résumé
Expériences relatives à la statique des fluides ; applications.
Introduction
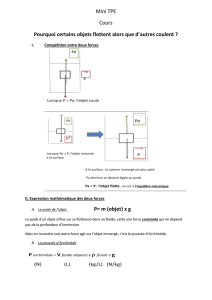
Pourquoi, quand je me baigne dans la mer morte, je flotte mieux que dans la mer méditerranée ?
Pourquoi le plongeur sous-marin ne doit pas remonter trop vite à la surface de l’eau ? Comment
fonctionne une presse hydraulique ? Je vais tenter de répondre à ces questions à travers ce montage
intitulé expériences relatives à la statique de fluides. Dans un premier temps, je vais mettre en évidence
le phénomène de pression atmosphérique. Ensuite, je vais essayer de retrouver le principe de la
statique des fluides. Nous verrons ensuite le théorème de Pascal et celui d’Archimède. Ces grandes lois
seront illustrées au fur et à mesure de l’exposé, par diverses applications.
Tout d’abord, je vais définir le sujet de l’étude à laquelle il m’est demandé de répondre. La statique des
fluides est un domaine de la mécanique des fluides qui s’intéresse aux fluides (donc aux gaz et aux
liquides) au repos, donc en équilibre. Un fluide est une substance qui n’a pas de forme propre et qui
épouse les parois du récipient qui le contient. Certains fluides sont compressibles, comme les gaz et
d’autres sont incompressible, comme les liquides.
I. Pression atmosphérique
I.1 Définition de la pression
La pression est une force par unité de surface : P(Pa=N/m2)=F(N)/S(m2). donc, à force égale, plus la
surface est petite, plus la pression est forte (cf dard de la guêpe qui arrive à trouer la peau et le fakir qui
est capable de s’allonger sur une planche de clous…). La pression s’exerce perpendiculairement à la
surface sur laquelle s’applique la force.
I.2 Mise en évidence de la pression atmosphérique
Nous vivons dans l’air qui est un fluide gazeux. Quelle est l’action de l’air sur nous et sur les objets qui
nous entourent ? Pour cela, je vais réaliser une expérience à l’aide d’une cloche à vide qui va nous
permettre de créer un environnement presque sans air.
Matériel nécessaire : Un ballon de baudruche; une cloche à vide reliée à une pompe à vide
1
On vient donc de montrer que l’ai qui nous entoure exerce une pression sur les objet
perpendiculairement à leur surface et que cette pression est responsable de la forme de certains objets.
I.3 Expérience de Magdebourg
Dans l’expérience précédente, nous avons « fait le vide » autour de l’objet. Que se passe t’il maintenant
si on réalise l’expérience inverse, c’est à dire si on fait le vide à l’intérieur d’un objet constitué de 2
hémisphères ? Il s’agit en fait de l’expérience historique réalisée par Otto von Guericke, bourgmestre de
Magdebourg en 1657.
Ordre de grandeur de la masse nécessaire pour séparer 2 sphères de diamètre 5 cm : 80 kg.
II. Pression statique au sein d’un fluide
II.1 Loi fondamentale de la statique des fluides
Nous allons essayer de vérifier la loi fondamentale de l’hydrostatique dans le cas d’un fluide dont la masse
volumique est constante dans les conditions de l’expérience : l’eau. dP= - ρgdz (axe z orienté vers le haut)
On utilise un manomètre à liquide muni de sa capsule manométrique que l'on plonge dans une cuve
remplie d'eau. (mesure de pression relative). Lorsque la capsule est dans l’air, il n’y a pas de
dénivellation dans le tube en U. La pression que l’on mesure est égale à la pression atmosphérique. Si
je plonge la capsule dans un liquide, le liquide exerce des forces de pression sur la membrane. On
observe une dénivellation dans le tube en U proportionnelle à la différence de pression.
 faire pivoter la capsule pour une profondeur donnée, la dénivellation est la même. Les forces de
pressions exercées sur la membrane sont bien perpendiculaires à sa surface, comme on l’a déjà vérifié
qualitativement avec le ballon de baudruche.
 on fait une ou 2 mesures devant le jury. Les autres on été faites en préparation.
 on trace la courbe h=f(H), soit p=f(H) et on obtient une droite. + la profondeur est importante, + la
pression est grande. P=P0 - gz (axe des z dirigé vers le haut et si ρ est constante). La pression varie
donc en fonction de l’altitude.
Application
Le plongeur sous-marin : lorsqu’il descend de 10m, la pression augmente de 1 bar. Les risques
encourus par le plongeurs sont plus importants lors de la remontée. En effet, il convient de bien vider
ses poumons. Comme la pression extérieure diminue, le volume de gaz contenu dans le poumons
augmente. Risque d’explosion. Par exemple : poumons pleins (~ 5 litres) à 10 mètres, si la respiration
1
Fonctionnement de la pompe à vide : pour mettre en route : fermer l’évacuation, ouvrir l’arrivée, mettre en route la
pompe. Pour arrêter : fermer l’arriver et arrêter la pompe

est bloquée jusqu'à la surface, le volume d'air a augmenté jusqu'à 10 litres, ce qui correspond à un
éclatement des poumons.
Illustration
Vases communicants de différents volumes. Fluide coloré. Quelle que soit la forme du récipient, la
surface libre de l’eau est toujours à la même altitude = surface isobare (p=patm).
II.2 Théorème de Pascal
II.2.1 Enoncé : la pression se transmet intégralement et instantanément dans tout fluide
incompressible. Expérience du tricol rempli d’eau (à ras bord)
II.2.2 Application : la presse hydraulique (Quaranta I p.330)
Dans 2 tubes de section différente, on a égalité des pressions : F1/S1=F2/S2. Si le piston 1 se déplace de
x1, alors le piston 2 se déplace de x2 tel que S1x1=S2x2. Une petite force F1 sur le cylindre de petite
section peut engendrer une force F2 importante. Le déplacement sera grand en x1 et plus petit en x2.
III. Poussée d’Archimède
III.1 Enoncé (Quaranta I p.197)
Tout corps immergé dans un fluide en équilibre subit de la part de celui-ci une force de poussée
verticale dirigée vers le haut, d’intensité égale au poids du volume de liquide déplacé et
appliquée au centre de masse C (ou de poussée) de ce fluide déplacé.
III.2 Vérification du théorème d’Archimède (Quaranta I p.198 – Bellier p.294 – Duffait p.255)
On accroche 1 cylindre plein et un cylindre creux de même volume au plateau d’une balance.
C’est la poussée d’Archimède qui explique que l’on flotte lorsqu’on est dans l’eau et que l’on flotte encore mieux
dans de l’eau salée qui a une masse volumique supérieure à celle de l’eau, d’où le fait que l’on flotte mieux en mer
morte que dans sa baignoire !!!
III.3 Le Baroscope (Quaranta I p.430 – Duffait p.255 – Bellier p.294)
On a vu que la poussée d’Archimède s’applique dans un fluide incompressible comme l’eau. Est-ce qu’elle
s’applique dans un autre fluide tel que l’air ?
On réalise l’équilibrage de l’ensemble (somme des moments = 0).
Que va t’il se passer lorsqu’on va enlever l’air grâce à une cloche à vide ? de quel côté va pencher la balance ? Si
la poussée d’Archimède s’applique aussi dans l’air, elle sera plus forte du côté de la boule la plus volumineuse. On
peut donc prévoir que la balance va pencher du côté de la boule de + grand volume. La poussée d’Archimède
s’applique donc dans tous les fluides.
III.4 Application : mesure de la masse volumique de la glycérine (Quaranta I p.113 – Duffait
p.256) objet : rondelle de cuivre d’environ 80g.  
 (dans les tables : 1,26 g/mL)
III.5 Application : le sous-marin (Quaranta I p.113 – Bellier p.294)
Illustré par la manip du ludion. Lorsqu’on appuie sur la membrane, on augmente la pression : le ludion
se remplit d’eau. Le poids étant plus important que la poussée d’Archimède, il descend. Si on arrête la
pression, il se vide et remonte, la poussée d’Archimède étant plus grande que le poids. C’est le principe
de fonctionnement des sous-marins qui remplissent leurs ballasts d’eau pour plonger ou d’air pour
refaire surface. Il y a équilibrage ou déséquilibrage constant entre poussée d’Archimède et poids.
Le thermomètre de Galilée fonctionne également sur ce principe : c’est un outil de mesure de la
température, basé sur le principe de la poussée d'Archimède et de la dilatation de la matière. Sur
chaque objet flottant est indiqué une valeur de température. Des objets flottants évoluent dans un
liquide, souvent de l'alcool. Ils ont tous le même volume V mais des masses différentes. Notons m la
masse de l'un de ces objets. Dans le liquide il est soumis à son poids P = mg et à la poussée
d'Archimède Π (opposé du poids du volume de fluide déplacé) qui s'écrit Π = ρ.V.g où ρ est la masse
volumique du fluide dans le tube. Cette masse volumique ρ dépend de la température : en général, elle
diminue lorsque la température augmente... donc la poussée d'archimède diminue quand la température
augmente. Supposons qu'au départ la température est faible, alors Π est supérieure à P et l'objet flotte.
Si on augmente la température Π diminue et il arrive un moment, à une certaine température T, où P
devient supérieur à Π : l'objet commence alors à couler. Ainsi plus l'objet est léger, plus il lui faut une
température élevée pour couler. Il suffit donc de fabriquer des objets de masses différentes et de même
volume et de calculer à quelle température ils coulent. (il faut avoir la fonction ou le graphe de ρ en
fonction de T).
Conclusion : La statique des fluides est un domaine d’étude important car nous vivons au milieu de
fluides : l’air ou l’eau. La pression augmente avec la profondeur (les plongeurs le savent bien) et diminue
avec l’altitude (en haute montage, la pression est + faible) : c’est le principe de l’hydrostatique. Nous
l’avons vu, le comportement des fluides compressibles et incompressibles est différent. On exploite
surtout, dans la pratique, la transmission de pression au moyen des fluides compressibles. Enfin, la
poussé d’Archimède a de nombreuses application et explique le phénomène d’équilibre des corps dans
un fluide.