ANGLES ET PARALLÉLISME EXERCICES

ANGLES ET PARALLÉLISME
EXERCICES
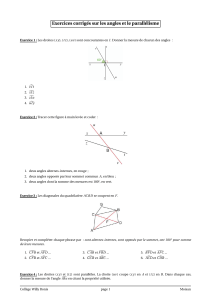
Exercice 1. Compléter le tableau suivant :
opposés par le sommet alternes-internes correspondants
Exercice 2. Compléter le tableau suivant :
opposés par le sommet alternes-internes correspondants
Exercice 3. Sur chaque figure coder un second angle de façon à obtenir deux angles alternes-
internes.
― 1 ―

Exercice 4. Sur chaque figure coder un second angle de façon à obtenir deux angles correspondants.
Exercice 5. Sur chacune des figures suivantes les droites (xy) et (zt) sont parallèles ; calculer les
mesures des angles inconnus.
Exercice 6. Sur chacune des figures suivantes démontrer que les droites (xy) et (zt) sont parallèles.
― 2 ―

Exercice 7. Sur la figure ci-contre, l'angle
̂
xAv
mesure 60°,
̂
vBt
mesure 121° et
̂
xDr
mesure 120°.
1°) La droite (AB) est-elle parallèle à la droite
(CD) ? Justifier la réponse.
2°) La droite (AD) est-elle parallèle à la droite
(BC) ? Justifier la réponse.
Exercice 8. Sur la figure ci-contre, les angles
̂
CAB
et
̂
ABD
sont égaux,
̂
xCv
mesure 60°. Calculer la
mesure de l'angle
̂
vDt
.
Exercice 9. Les droites (uv) et (rs) sont
perpendiculaires entre elles,
̂
rAx
mesure 30° et
̂
uBt
mesure 60°. Démontrer que les droites (xy) et
(zt) sont parallèles entre elles.
Exercice 10. Les droites (xy) et (zt) sont parallèles
entre elles,
̂
yAB
mesure 40° et
̂
BCt
mesure 30°.
Calculer l'angle
̂
ABC
.
Exercice 11. Les droites (xy) et (zt) sont parallèles
entre elles,
̂
vAy
mesure 40° et
̂
uBv
mesure 70°.
Démontrer que [Bu) est la bissectrice de l'angle
̂
zBv
.
― 3 ―

Exercice 12. Tracer un triangle ABC avec
̂
ABC
=120°, AB = 5 cm et BC = 10 cm. Tracer la
bissectrice (d) de l'angle
̂
ABC
. Tracer la droite passant par C et parallèle à (AB), elle coupe (d) au
point D. Calculer l'angle
̂
BDC
.
Exercice 13. ABCD est un trapèze de bases [AB] et [CD], de plus
̂
ABC
= 120°. Calculer la mesure
de l'angle
̂
BCD
.
Exercice 14. Une démonstration de la propriété sur la somme des angles d'un triangle. Etant donné ABC
un triangle quelconque, traçons la droite (xy) parallèle à (BC)
passant par A.
1°) Démontrer que les angles
̂
xAB
et
̂
ABC
sont égaux.
2°) A quel angle est égal
̂
ACB
? Justifier.
3°) Que peut-on dire des angles
̂
xAB
̂
BAC
̂
yAC
?
4°) Que peut-on en déduire des angles
̂
ABC
̂
BAC
̂
ACB
?
5°) Compléter la propriété ainsi démontrée : « Les trois angles
d'un triangle sont ... »
6°) Enoncer d'une autre façon cette propriété.
Exercice 15. Au IIIe siècle avant Jésus-Christ, le mathématicien Grec Eratosthène réussit à évaluer le
périmètre de la Terre. Il observa que
le jour du solstice d’été, à midi, les
rayons du soleil éclairaient le fond des
puits à Syène, tandis qu'au même
moment à Alexandrie un obélisque
formait une ombre. Ainsi les rayons
du Soleil étaient à la verticale à Syène
et au même moment inclinés de 7° 12'
(soit 7,2°) avec la verticale à
Alexandrie. Eratosthène savait que la
distance entre les deux villes était de
5000 stades (1 stade ≈ 157,5 mètres) ; il
supposa de plus que ces deux villes
étaient situées sur le même méridien
et que les rayons du Soleil étaient
parallèles.
1°) Comment Erastothène démontra
que
̂
ACS
=
̂
AOH
?
2°) Eratosthène fit ensuite un raisonnement de proportionnalité : La distance entre les parallèles
séparant les villes est proportionnelle à la mesure de l'angle dont le sommet est au centre de la Terre.
Compléter le tableau de proportionnalité suivant :
Angles (°)
̂
ACS
 7,2 ...
Distances (km) ... Périmètre de la Terre
3°) En déduire quel est le périmètre de la Terre trouvé par Eratosthène. Aujourd'hui on estime ce
périmètre à 40 070 km.
― 4 ―