Ferromagnétisme

I Introduction 1
1 Présentation 1
2 Principe de l’étude 1
II Observation du cycle d’hystérésis 2
III Courbe de première aimantation 5
IV Tracé des cycles d’hystérésis 6
V Étude des pertes d’énergie par hystérésis 8
1 Étude théorique 8
2 Étude expérimentale 9
TP Conversion de puissance – 1
Ferromagnétisme
I Introduction
1 Présentation
Les objectifs de ce T.P. sont :
• Tracer expérimentalement les cycles d’hystérésis de deux matériaux magnétiques.
• Mesurer les excitations coercitives, les propriétés rémanentes et à saturation de ces deux matériaux.
• Tracer expérimentalement la courbe de première aimantation d’un de ces matériaux magnétiques.
• Mesurer les pertes énergétiques par hystérésis dans ces matériaux.
2 Principe de l’étude
On considère un échantillon ferromagnétique en forme de tore, de circon-
férence moyenne ℓ, de section 𝑠.
Le circuit primaire comporte 𝑁1spires bobinées sur le tore, parcourues
par un courant d’intensité 𝐼.
Le circuit secondaire comporte 𝑁2spires bobinées sur le tore parcourues
par une intensité négligeable.
𝐸(𝑡)
𝐼(𝑡)
𝑈(𝑡)
On suppose que les champs ⃗ 𝐻,⃗ 𝐵et ⃗ 𝑀sont orthoradiaux et de norme uniforme dans le matériau :
⃗
𝐻 = 𝐻 ⃗𝑒⃗ 𝐵 = 𝐵 ⃗𝑒⃗ 𝑀 = 𝑀 ⃗𝑒
Montrer que l’excitation magnétique dans le tore est liée à l’intensité dans le circuit primaire :
⃗
𝐻(𝑡) = 𝑁1𝐼(𝑡)
ℓ⃗𝑒
et que la tension au secondaire est liée au champ magnétique ⃗ 𝐵 = 𝐵 ⃗𝑒par :
𝑈(𝑡) = −𝑁2𝑠d𝐵
d𝑡
En appliquant le théorème d’Ampère
𝐻ℓ = 𝑁1𝐼
𝐻 = 𝑁1𝐼
ℓ
En utilisant la loi de Faraday

2/9 Ferromagnétisme
𝑒 = 𝑈 = −𝑁2𝑠d𝐵
d𝑡
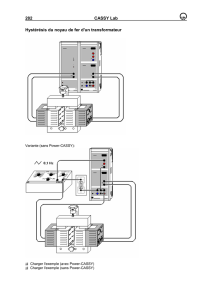
Les circuits que nous allons étudier expérimentalement ont une géométrie un
peu plus complexe mais sont décris par des équations analogues.
Le circuit magnétique est constitué de plaques en forme de E imbriquées les
unes dans les autres. Les deux bobines sont placées sur la branche centrale.
Pour que les champs ⃗ 𝐻,⃗ 𝑀et ⃗ 𝐵soient de norme uniforme, la section 𝑠de la
branche centrale est le double de toutes les autres.
On note 𝑙 = 12,6cm la longueur moyenne des lignes de champs (représentées
sur la figure ci-contre) et 𝑠 = 2,00cm2la section moyenne du circuit magnétique.
Les deux matériaux utilisés sont notés :
• 1W7 : tôles d’acier au silicium ;
• M6X : tôles d’acier à grains orientés.
II Observation du cycle d’hystérésis
Montage 1 : Tracé du cycle d’hystérésis
âLe générateur est un alternostat qui délivre une
tension sinusoïdale, de fréquence 𝑓 = 50Hz,
d’amplitude variable entre 0 et 12V.
âLe bobinage primaire comporte 𝑁1= 200
spires.
âLe bobinage secondaire comporte 𝑁2= 200
spires.
â𝑅 = 10Ω
â𝑅′=100kΩ
â𝐶 = 1µF
𝑈(𝑡)
𝑅′
𝐶
𝑉
𝑅
𝑉1(𝑡)
𝐸(𝑡)
𝑌1
𝑌2
La tension mesurée par la voie 1 est : 𝑉1= 𝑅𝐼 L’excitation magnétique pourra donc être estimée grâce à :
𝐻 = 𝑁1
𝑅ℓ𝑉1
Le circuit 𝑅′𝐶se comporte comme un intégrateur pour la fréquence utilisée :
𝐵 = −𝑅′𝐶
𝑁2𝑠𝑉
Rmq : L'expression de H ne faisant intervenir que le courant dans le bobinage du primaire est
valable si la contribution du secondaire est négligeable (soit si N2.i2 << N1.i1).
Ceci sera obtenu en plaçant une faible résistance dans le circuit primaire, une très forte dans
le circuit secondaire.

Ferromagnétisme 3/9
1. Relever les oscillogrammes en mode XY pour les deux matériaux.
1W7
Sensibilité vert. :
Sensibilité horiz. :
M6X
Sensibilité vert. :
Sensibilité horiz. :
2. Utiliser les courbes précédentes pour estimer la valeur de l’excitation coercitive 𝐻pour 1W7.
Les tensions sont mesurées au curseur 𝑉= 475mV
On en déduit 𝐻=1
ℓ
Donc 𝐻=75,4A/m
3. Utiliser les courbes précédentes pour estimer la valeur du champ rémanent 𝐵pour 1W7.
Les tensions mesurées aux curseurs 𝑉=213mV
On en déduit 𝐵=′
2𝑉
Donc 𝐵=0,533T
4. Utiliser les courbes précédentes pour estimer la valeur de l’excitation coercitive 𝐻pour M6X.

4/9 Ferromagnétisme
Les tensions sont mesurées au curseur 𝑉= 0,159V
On en déduit 𝐻=1
ℓ
Donc 𝐻=25,2A/m
5. Utiliser les courbes précédentes pour estimer la valeur du champ rémanent 𝐵pour M6X.
Les tensions mesurées aux curseurs 𝑉=0,249V
On en déduit 𝐵=′
2𝑉
Donc 𝐵=0,621T
6. Regrouper les résultats dans le tableau suivant, indiquer si les matériaux sont durs ou doux.
1W7 M6X
𝐻75,4A/m 25,2A/m
𝐵0,533T0,621T
doux doux

Ferromagnétisme 5/9
III Courbe de première aimantation
On se propose la courbe de première aimantation. Pour cela, on effectue des cycles d’amplitude lentement croissante et l’on
note le sommet de chacun de ces cycles. Ces points appartiennent à la courbe de première aimantation.
Relever cette courbe de première aimantation ci-dessous pour 1W7.