Le condensateur – Le dipôle RC série (1)

Physique – Terminale S
Chapitre 6
Travaux Pratiques n°6a
Le dipôle RC (1) - Correction
1
Le condensateur – Le dipôle RC série (1)
Etude de la charge du condensateur (correction)
1 – Deux nouveaux dipôles !
On réalise le montage suivant.
Ce montage assure une différence de potentiel aux bornes d’une association {dipôle + lampe}. Nous
pouvons, à l’aide de l’observation du comportement des lampes, en déduire quelques propriétés de chaque
dipôle. Les trois dipôles, résistance R, condensateur C et bobine L, sont des récepteurs.
Le condensateur C et la bobine L ont un comportement singulier par rapport à la résistance R. En effet, il
apparaît dans la branche qui le contient des phénomènes caractéristiques.
Le condensateur, à l’allumage, se charge électriquement et une fois sa charge terminée, très
rapidement, il coupe le circuit et la lampe L1 s’éteint ; à la rupture, il se décharge brutalement dans la
lampe et restitue l’électricité qu’il a stockée en provoquant le flash observé
La bobine, elle, s’oppose à l’établissement et à la rupture du courant électrique en ralentissant
l’allumage et l’extinction de la lampe L3.
Ces deux composants laissent entrevoir de nouvelles possibilités en électricité, si nous apprenons à les
maîtriser. Pour le condensateur, c’est le but de ce TP.
2 – A la découverte du condensateur : charge à courant constant
2.1 – Le condensateur
Un condensateur est un dipôle constitué de deux plaques conductrices A et B, appelées armatures, séparées
par un matériau isolant appelé diélectrique.
A la fermeture de l’interrupteur k, on constate
– L1: la lampe s’allume immédiatement et s’éteint
très rapidement
– L2: la lampe s’allume immédiatement
– L3: la lampe s’allume avec un léger retard
A l’ouverture
– L1: la lampe se rallume subitement et s’éteint
aussitôt (flash)
– L2: la lampe s’éteint immédiatement
– L3 : la lampe s’éteint avec un léger retard
AB
Symbole du condensateur
K+
R
L
–
rouge
bleu
jaune
U = 12 V
L
CL1
L2
L3

Physique – Terminale S
Chapitre 6
Travaux Pratiques n°6a
Le dipôle RC (1) - Correction
2
2.2 – Montage expérimental
La position 1 correspond à la charge du condensateur. La position 2 permet de le décharger.
Le circuit réalisé est équivalent au circuit simplifié suivant :
On travaillera à partir du fichier d’acquisition disponible en TP dans vos documents (Devoirs/Physique).
Le but est ici d’étudier les grandeurs physiques caractéristiques du condensateur : la tension Uc à ses bornes,
l’intensité i qui le traverse et la charge accumulée sur ses armatures.
La centrale d’acquisition possède de nombreuses voies d’acquisition (EA0, EA1, EA2, etc…) mais une seule
masse, qui doit être commune à toutes les acquisitions.
Pour étudier l’intensité i du circuit de charge, nous utilisons la résistance R : en étudiant la tension à ses
bornes, donnée par EA0, nous pourrons en déduire, avec la loi d’Ohm, l’intensité i qui circule dans le circuit,
0
R
U
EA
i
R R
Pour étudier le condensateur lui-même, il nous faut avoir accès à la tension à ses bornes, Uc ; s’agissant d’un
récepteur électrique, il s’agit de la tension positive UAB (convention récepteur). Le branchement de
l’acquisition impose la mesure de EA1 = UBA = –UAB ; il faudra donc tenir compte de cette contrainte dans
l’étude que nous allons mener.
2.3 – Evolution temporelle de la tension Uc = UAB
Définir une nouvelle variable Uc telle que Uc = UAB = –EA1 (feuille de calcul : Uc = –1*EA1).
Tracer la courbe Uc(t). → voir courbe n°1 en annexe
La tension UC est proportionnelle à la durée Δt de la charge. Lorsque le condensateur est chargé, la tension
Uc atteint la valeur UAB,max = 10 V.
2.4 – Evolution temporelle de la charge qA
2.4.1 – Obtention de la courbe qA(t)
Définir, à partir de l’acquisition EA0, une nouvelle variable i correspondant à l’intensité dans le circuit.
Feuille de calcul : « R = 68000 » puis « i = EA0/R »
Tracer i(t) en vérifiant que « t » est bien la variable de i. → voir courbe n°2 en annexe
Dans le circuit étudié, i = io≈ 150 µA lors de la charge et lorsque le condensateur est chargé, i = 0 (circuit
ouvert).
4,0 V
C = 470 µF
68 kΩ
12
0
P
N
A
B
+ +
– –
R
i = cte
voie
EA
1
i
Source idéale
de courant
Rd
5 kΩ
voie
EA0
Réglages Latis Pro
Total : 50 s
Points : 1 000
Déclenchement : EA1
Sens : descendant
Seuil : – 0,05 V
UR = EA0
UBA = EA1

Physique – Terminale S
Chapitre 6
Travaux Pratiques n°6a
Le dipôle RC (1) - Correction
3
On peut remonter à la valeur de la charge qA par la relation
A
dq
i
dt
En effet, si i(t) est la dérivée de qA(t) par rapport au temps, qA(t) est la primitive résultant de l’intégration de
i(t). Latis Pro peut calculer l’intégrale d’une courbe.
A partir de la courbe i(t), utiliser le traitement d’intégration de Latis Pro pour obtenir qA.
On se place dans la fenêtre contenant la représentation de i(t) ; par Traitements > Calculs spécifiques >
Intégrale » il est possible d’obtenir la courbe cherchée.
Tracer qA(t), en vérifiant bien que la variable de qA est « t ». → voir courbe n°3 en annexe
La charge qA est proportionnelle à la durée Δt de la charge. Lorsque le condensateur est chargé, la charge qA
atteint la valeur qA,max = 4,70 mC.
C’est logique, puisque I = Io = constante, on a par
A
dq
i
dt
 la relation qA = Io Δt. Cette relation n’est valable
que pour la montée de la courbe, car une fois le condensateur chargé, l’intensité s’annule.
2.4.2 – Notion de capacité
Tracer, sur une nouvelle fenêtre graphique, qA(Uc). → courbe n°4 en annexe
Modéliser la courbe obtenue et relever les paramètres de modélisation.
Conclure.
Sur la durée Δt, nous avons UAB = Uc = ku Δt et qA = Io Δt ; écrivons
AB A
u o
U q
t
k I
et il vient
o
A AB AB
u
I
q U k U
k
On retrouve la proportionnalité entre la charge qA du condensateur et la tension UAB à ses bornes.
La constante de proportionnalité est appelée capacité du condensateur ; notée C, elle s’exprime en farads (F)
si la charge est en coulombs (C) et la tension en volts (V).
Donnez la valeur expérimentale de la capacité C du condensateur et conclure en comparant avec la valeur
donnée par le constructeur sur le composant.
La modélisation indique une relation de proportionnalité qA = a x Uc avec a = 465,5.10–6 C.V–1. Sur le
condensateur, nous lisons C = 470 µF = 470.10–6 F. Nous avons un écart raisonnable à la valeur donnée par
le constructeur,
470 465,5
100 1%
470
écart
En convention récepteur, nous écrirons :
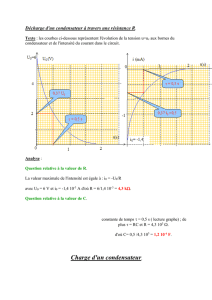
3 – Charge d’un condensateur à tension constante : réponse à un échelon de tension
3.1 – Montage expérimental
On réalise le montage suivant.
Modélisation : linéaire
qA = a*Uc
a = 465,5E-6
corr. 0,99928
A
i
B
UAB
qA = C x UAB > 0
volt (V)
coulomb (C)
farad (F)

Physique – Terminale S
Chapitre 6
Travaux Pratiques n°6a
Le dipôle RC (1) - Correction
4
Indiquer, sur le schéma, les branchements de EA0 et EA1 permettant d’acquérir respectivement la tension
aux bornes de la résistance et la tension aux bornes du condensateur. N’oubliez pas la masse !!
Vérifier, au voltmètre, qu’initialement le condensateur est déchargé : quelle doit être la tension à ses bornes ?
Si le condensateur est initialement déchargé, ses armatures ne doivent présenter aucune charge électrique : la
différence de potentiel (tension Uc) à ses bornes doit donc être nulle !
A l’instant t = 0, l’interrupteur est basculé en position 1 : l’ensemble RC est soumis à une tension constante E
= 5,0 V. On dit qu’on charge le condensateur.
3.2 – Evolution temporelle de la tension UAB = Uc
A partir de l’acquisition de EA1, définir une nouvelle variable Uc correspondant à UAB (feuille de calcul : Uc
= –1*EA1)
Tracer Uc(t). → Voir courbe n°5 en annexe
La tension Uc augmente au cours du temps ; il s’agit d’un régime transitoire qui correspond à la charge du
condensateur, et un régime permanent s’établit, avec UAB = 5,0 V, lorsqu’il est chargé.
Modéliser la courbe Uc(t) obtenue, et relever les paramètres de la modélisation.
Uc=A*(1-Exp(-(Temps-Δ)/τ))+V0
A = 5
Δ = 0
τ = 50E–3
V0 = 2,021E-9
En utilisant notamment les phénomènes déjà étudiés, exprimer les paramètres de la modélisation en fonction
de E, R et C.
Le paramètre A est très proche de la tension fournie par le générateur, E = 5,0 V.
Le paramètre τ est homogène à une durée car l’argument de l’exponentiel doit être adimensionné. Travaillons
sur les grandeurs R et C :
U V
R
I A
Or,
dq C
A I
dt s
  donc
5,0 V
C = 10 µF
5 kΩ
12
0
P
N
A
B
+ +
– –
R
i
Réglages Latis Pro
Nombre de points : 500
Total temps : 400 ms
Déclenchement : source EA1
Sens : descendant (EA1 décroît)
Seuil : – 0,05 à – 0,1 V
+
EA0
EA1
masse

Physique – Terminale S
Chapitre 6
Travaux Pratiques n°6a
Le dipôle RC (1) - Correction
5
.
V V s
R
A C
q C
C
U V
On voit apparaître que le produit R x C est homogène à une durée :
3 6 3
5.10 10.10 50.10
R C s
    . Ce
produit se rapproche de la valeur de τ donnée par la modélisation. Nous pouvons donc proposer
( ) 1
t
Uc t E e
avec
R C
Comment peut-on appeler le produit τ = R x C ? Comment le déterminer graphiquement ?
En radioactivité, l’exponentielle temporelle était déjà intervenue : la constante τ était alors appelée constante
de temps du système.
Nous avions vu qu’il était possible de la déterminer graphiquement de deux façons,
à l’aide de la tangente à l’origine
L’équation de cette tangente s’écrit
00
t
tt
dUc E E
U t e t t
dt
Cette droite coupe l’asymptote U = E de la courbe Uc(t) pour l’égalité
E
t E
c’est-à-dire à t = τ.
à l’aide des 63%
Cherchons la valeur de la tension Uc(t) atteinte pour t = τ :
1
1 1 0,63
Uc t E e E e E
On voit qu’à t = τ, la tension aux bornes du condensateur a atteint 63 % de sa valeur maximale à la charge, E.
3.3 – Evolution temporelle de l’intensité i
A l’aide de l’acquisition de
EA0, définir une nouvelle
variable i correspondant à
l’intensité.
Tracer i(t). → voir courbe n°6 en annexe
L’intensité i est un fonction décroissante du temps. Elle décroît d’une valeur io = 0,1 mA (régime transitoire)
à une valeur nulle lorsque le condensateur est chargé (régime permanent).
Modéliser cette courbe et relever les paramètres de modélisation.
Uc=a*Exp(b*Temps)
a = 1E–9
b = –20
En utilisant notamment les phénomènes déjà étudiés, exprimer les paramètres de la modélisation en fonction
de E, R et C.
A = E/R = 1 µA et b = RC = 20 ms