LYCEE ZAHROUNI-TUNIS- SCIENCES PHYSIQUES 4ème année

E
K
L2
L1
R
L, r
figure-2-
LYCEE ZAHROUNI-TUNIS-
SCIENCES PHYSIQUES
4ème année
Induction électromagnétique
Exercice 1
On réalise le circuit électrique comprenant en série :
- une bobine purement inductive d’inductance L = 0,5 H,
- Un résistor de résistance R = 50 ,
- Un générateur basse fréquence (GBF) délivrant une tension
triangulaire.
Un oscilloscope branché comme c’est indiqué sur la figure-1- où
le sens positif du courant d’intensité i, les tensions uR et uL
respectivement aux bornes du résistor et de la bobine, ont été
représentés. La sensibilité horizontale est réglée sur 10 ms.div-1 et la sensibilité verticale de la voie Y2
sur 2 V.div-1. On obtient sur cette voie inversée, l’oscillogramme de la figure-2-a-
1. Des tensions uL et uR, préciser en le justifiant, celle qui permet de
suivre l’évolution de l’intensité i du courant.
2. Montrer que l’intensité i du courant s’écrit :
- pour la première demi-période i(t) = 8t + b1 ;
- pour la deuxième demi-période i(t) = -8t + b2 où t en s, i en A,
b1 et b2 sont deux constantes que l’on ne déterminera pas la valeur.
3. Pour chacun de ces deux demi-périodes, calculer la force
électromotrice d’auto-induction e dans la bobine.
4. Tracer sur la figure-2-b- l’oscillogramme obtenu sur la voie Y1
réglée sur la sensibilité verticale 2V.div-1.
Exercice 2
1°) Soit le circuit de la figure-2-, constitué d’un générateur de
tension contenu, d’un interrupteur K, de 2 lampes identiques L1 et L2,
d’un résistor de résistance R=0,5 associé en série avec la lampe L1
et d’une bobine d’inductance L=1H et de résistance r=0,5 associée en série
avec la lampe L2.
Lorsqu’on ferme l’interrupteur K, on constate que l’une des deux lampes s’allume
après un retard t. Identifier cette lampe et expliquer le phénomène mis en jeu.
2°) On alimente maintenant la bobine par un générateur de courant variable i(t)
dont la représentation est donnée par la figure-3-
a) Déterminer la période de i(t) et établir ses expressions sur une
période T.
b) Déterminer les valeurs de la fem induite e(t) sur une période T
c) En déduire les expressions de la tension ub(t) aux bornes de la
bobine sur une période T.
d) Représenter, soigneusement et avec deux couleurs différentes,
les tensions e(t) et ub(t) pour t [0 ; T] sur un même graphe
Exercice 3
I - Une bobine d’inductance L et de résistance négligeable est
reliée à un microampèremètre, comme l’indique la figure ci-contre,
On rapproche l’aimant vers la bobine,
1- Quel est le phénomène observé ?
2- Indiquer le sens de circulation du courant induit dans la bobine.
3- Préciser l’inducteur et l’induit.
II - Avec la bobine précédente, on branche en série un résistor de
résistance R=10 KΩ et un générateur basse fréquence (G.B.F à masse
flottante ) qui délivre une tension triangulaire alternative. Sur l’écran
d’un oscilloscope bicourbe, on visualise la tension uAB sur la voie YA et la tension uCB sur la voie YB
(figure 4)
1- On note i(t) l’intensité instantanée du courant qui traverse le circuit, son sens positif choisi est
indiqué sur le schéma du montage.
a- Montrer, sans calcul, que la bobine est le siège d’un phénomène d’auto-induction.
b- Montrer que la tension aux bornes de la bobine est
Figure-2-
a-
Figure-1-
GBF
R
L
Y1
Y2
uL
uR
i
i
figure-3-
1
2
3
4
5
6
0
4
i (A)
t (s)
µ
A
Bobine
Aimant droit
N

c- Justifier littéralement l’allure de la tension sur la voie YA.
2- Les réglages de l’oscilloscope sont :Sensibilité verticale de la voie YA : 0,2V.div-1 Sensibilité
verticale de la voie YB : 2V.div-1 Sensibilité horizontale : 0,2 ms.div-1
A partir des oscillogrammes :
a- Calculer la période T et la fréquence N des tensions.
b- Pendant la première demi-période, déterminer les expressions de uAB et de uCB en fonction du
temps.
c- En déduire la valeur de l’inductance L de la bobine. Puis indiquer sa signification physique.
Exercice 4
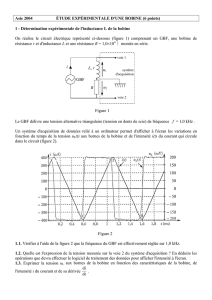
Dans le but de déterminer l’inductance L d’une bobine de résistance r = 9  , on réalise le circuit de la
figure ci-contre, comportant, montés en série avec cette bobine :
 Un générateur basse fréquence (GBF) délivrant une tension triangulaire.
 Un résistor de résistance R réglable.
On branche un oscilloscope bicourbe de manière que sa masse est
reliée au point M et ses voies d’entrée A et B sont reliées
respectivement aux points P et Q.
1. Définir l’inductance d’une bobine.
2. En tenant compte du sens positif choisi pour le courant, établir
les expressions de :
 la tension uPM en fonction de l’intensité i du courant dans le
circuit et de sa dérivé première par rapport au temps
Error!
;
 la tension uQM en fonction de i.
3. En actionnant la touche « ADD » de l’oscilloscope, on observe
sur l’écran de l’oscilloscope, la tension somme des tensions
enregistrées sur les voies A et B : uPQ = uPM + uQM .
3.1. Etablir l’expression de la tension uPQ en fonction de i et
Error!
.
3.2. Déterminer la valeur R0 de la résistance R pour que la tension uPQ soit égale au terme L
Error!
.
4. On fixe la résistance R à la valeur R0 et on visualise successivement les tensions uQM et uPQ. On
obtient les chronogrammes de la figure.ci - dessous avec les réglages suivants :
 Sensibilités sur les deux voies : 1V/division ;
 Base de temps : 2 ms/division ;
 En l’absence de tension, les traces horizontales sont au centre de l’écran.
4.1. Etablir la relation     
 .
4.2. Déterminer la valeur de l’inductance L de la bobine.
G
A
B
Fig 4
YB
YA
R
uPQ
M
P
Q
Voie A
Voie B
i
uPM
uQM
GBF
L, r
Masse