Le modèle de Hodgkin-Huxley

Le modèle de Hodgkin-Huxley
François Boulier
21 octobre 2016
1 Les équations
Les équations du modèle sont les suivantes [3], [5, chapter 5, page 224].
CM
dV
dt=−gKn4(V−VK)−gNa m3h(V−VNa)−gL(V−VL) + Iapp ,
dn
dt=αn(V) (1 −n)−βn(V)n ,
dm
dt=αm(V) (1 −m)−βm(V)m ,
dh
dt=αh(V) (1 −h)−βh(V)h .
CM= 1,gK= 36,gNa = 120,gL= 0.3,VK=−77,VNa = 50,VL=−54.4.
αn(V)=0.01 (−V−55)/(exp((−V−55)/10) −1) ,
βn(V)=0.125 exp((−V−65)/80) ,
αm(V)=0.1 (−V−40)/(exp((−V−40)/10) −1) ,
βm(V)=4exp((−V−65)/18) ,
αh(V)=0.07 exp((−V−65)/20) ,
βh(V) = 1/(1 + exp((−V−35)/10))
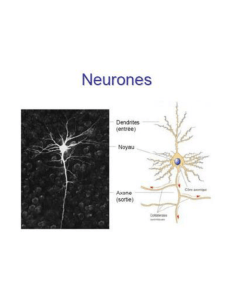
L’équation principale est la première, qui donne l’évolution du potentiel de la membrane. Le
membre droit de cette équation fait figurer des courants ioniques dus à des échanges d’ions K+et
Na+entre les milieux intra et extra-cellulaires. Le neurone est une cellule excitable [5, chapter 5,
page 195]. Une simulation apparaît Figure 1.
2 Vérification des dimensions
Commençons par vérifier les dimensions des équations. Une présentation très claire des bases
d’électricité nécessaires est disponible dans [2, chapter 1], accessible à cette URL-ci. Une charge Q
se mesure en C. Un courant Ise mesure en A =C s−1. Un potentiel Vse mesure en V =J C−1. Il
faut un joule d’énergie pour déplacer un coulomb à travers une différence de potentiel de un volt.
Pour créer une différence de potentiel, il suffit de séparer deux charges. Une capacité Cest une
mesure en F de la charge à déplacer pour atteindre une différence de potentiel donnée :
Q=C V . (1)
1

−80
−60
−40
−20
0
20
40
60
0 10 20 30 40 50 60
V
t
7
1+e20−t
Figure 1–La réponse de V(t)en fonction d’un stimulus Iapp. Les oscillations (à peu près les
mêmes) apparaissent pour un stimulus d’intensité supérieure à une valeur critique comprise entre
5et 7. En réponse à un stimulus d’intensité inférieure, les oscillations s’amortissent rapidement.
Il est toutefois difficile de parler de seuil. Voir [4, chapter 1] à ce sujet. La valeur Veq =−65 mV
correspond au potentiel au repos de la membrane.
La loi (empirique) d’Ohm V=R I peut aussi s’exprimer avec des conductances gen S = Ω−1:
I=g V . (2)
Dérivons l’équation (1). Le membre gauche de l’équation dérivée est la dérivée par rapport à tde Q
et a la dimension de C s−1. C’est donc un courant. Supposons la capacité Cconstante. Le membre
droit de l’équation dérivée s’écrit
CdV
dt
et a donc aussi la dimension d’un courant.
On voit donc que le membre gauche de la première équation du modèle de Hodgkin-Huxley a
la dimension d’un courant. La capacité de la membrane CMvaut 1µF cm−2[5, chapter 2, page 86].
La dimension du courant est en µA cm−2[5, chapter 5, page 206]. Pour que les dimensions soient
cohérentes, il faut que l’unité de temps soit la ms. Le membre droit de l’équation doit aussi être
une somme de courant en µA cm−2. C’est le cas pour le stimulus Iapp. C’est aussi le cas pour les
autres termes, qui sont des différences de potentiels (en mV), multipliées par des conductances (en
mS cm−2).
Un terme de la somme correspond au courant ionique dû au déplacement, à travers la membrane,
des ions K+. Un autre correspond au courant ionique dû aux ions Na+. Le troisième terme regroupe
les autres ions, principalement les Cl−. Les variables net msont des nombres sans dimension.
2

Elles représentent chacune la fraction ouverte de la population d’un certain type de canal ionique
(potassium ou sodium). La variable hreprésente une fraction fermée/inactivée de de la population
des canaux ioniques sodium.
3 Travail à réaliser
Écrire un fichier HodgkinHuxley.f consacré à ce problème. La variable tde ce document corres-
pond à la variable xdu support de cours. La dimension est n= 4. Les variables sont y1, y2, y3, y4=
V, n, m, h. Des conditions initiales possibles sont y1(0), y2(0), y3(0), y4(0) = −65,1
3,0,2 3. Prendre
pour intervalle de temps [x0, xend] = [0,60]. La fonction Iapp(t)doit être intégrée à la fonction
PROBLEM F. On peut prendre la fonction suivante :
Iapp(t) = 25
1 + e20−t.
4 Compléments sur le modèle de Hodgkin-Huxley
La membrane sépare le milieu intra-cellulaire du milieu extra-cellulaire. Voir par exemple
biochemreview.weebly.com/lipids.html. Elle a la structure d’un couche bilipidique, traversée
de protéines. Certaines de ces protéines sont des canaux ioniques (ion channels) : i) ils sélectionnent
les ions qu’ils transportent (ion selective) et ii) ils peuvent se fermer (gated). Plus précisément, ils
sont capables de s’ouvrir brièvement et se refermer ensuite. De plus, en présence d’un stimulus
prolongé, ils peuvent se mettre dans un troisième état, dit inactivé, qui les empêche de se réou-
vrir jusqu’à-ce que le stimulus cesse. Parmi les principaux stimuli, on trouve les changements de
potentiel de la membrane (voltage-gated channels) [1, chapter 11, page 668].
Les deux couches de la membrane peuvent être vues comme deux conducteurs séparés par une
fine couche d’isolant : un condensateur d’une capacité CM= 1 µF cm−2. Une membrane munie d’un
canal ionique peut être modélisée comme un circuit comportant un condensateur (la membrane),
en parallèle avec une résistance/conductance (le canal ionique) [2, chapter 1, page 10]. Note : ce
chapitre 1est accessible sur le web 1. La tension de la membrane est, par définition :
VM=Vi−Vo,(3)
où Vidésigne le potentiel du milieu intra-cellulaire et Vocelui du milieu extra-cellulaire. Le courant
passe par les canaux ioniques. Chaque canal ionique est vu comme une conductance élémentaire.
La conductance d’une membrane est la somme des conductances élémentaires des canaux ioniques.
C’est une mesure du nombre de canaux ouverts. Elle peut se mesurer expérimentalement. En
dérivant la relation Q=CMV(définition de la capacité, appliquée à la membrane), on trouve une
expression pour le courant Icond qui sort de la membrane, vue comme un condensateur :
Icond =dQ
dt=CM
dV
dt
·
La première équation du modèle pose que ce courant est égal à la somme du courant qui passe par
les canaux ioniques K+, Na+(plus les autres regroupés en un terme, assimilé à une fuite) et du
stimulus Iapp.
1. pub.ist.ac.at/Pubs/courses/2012/introductiontoneuroscience1/docs/LecturesMay13,15/Hille_
IonChannelsofExcitableMembranes_Chapter1.pdf
3

Intéressons-nous aux courants ioniques. Dans la première équation du modèle apparaissent des
constantes VK,VNa et VL. Ce sont des équilibres de Nernst. Voici l’idée, illustrée sur les ions K+.
Supposons pour simplifier que la tension de la membrane soit nulle et que les ions K+soient
beaucoup plus concentrés à l’intérieur qu’à l’extérieur de la cellule. Notons que cela implique la
présence d’ions A−dans le milieu intra-cellulaire en quantité suffisante pour compenser la charge
des ions K+et faire en sorte que la tension soit nulle. Supposons qu’on ouvre un canal ionique
sélectif pour K+. En raison de la différence de concentrations entre l’intérieur et l’extérieur de la
cellule, les ions K+vont avoir tendance à sortir de la cellule. Si ces ions n’étaient pas chargés
électriquement, les deux concentrations finiraient par s’équilibrer en devenant égales. Comme ils
sont chargés électriquement, à chaque fois qu’un ion K+sort, il rend le potentiel intra-cellulaire
un peu plus négatif : la tension de la membrane s’éloigne de zéro. Plus les ions K+sortent, plus
cette tension devient négative et plus elle tend à retenir les ions K+qui sont positifs. Arrivé à une
certaine tension, le flux d’ions s’arrête : c’est cette tension qu’on appelle l’équilibre de Nernst. Des
formules permettent de calculer ces équilibres [2, chapter 1, pages 14-15].
Les canaux ioniques les plus communs sont sélectifs pour les ions K+. Un important sous-
ensemble de ces canaux ioniques est formé des K+leak channels, qui sont tout le temps ouverts [1,
chapter 11, page 669]. La membrane au repos a donc un potentiel proche de l’équilibre de Nernst des
ions K+c’est-à-dire V=−65 mV ≃VK. En présence d’un stimulus, les canaux Na+passent dans
l’état ouvert et laissent rapidement entrer les ions Na+jusqu’à atteindre V≃VNa ≃56 mV. Les
canaux ioniques Na+se mettent alors dans l’état inactivé. Des canaux ioniques K+supplémentaires
s’ouvrent et aident les K+leak channels à ramener la membrane à V=−65 mV. Ce retour à
V=−65 mV remet les canaux ioniques Na+dans l’état fermé. Voir [1, chapter 11, pages 676-678].
Les canaux ioniques K+et Na+ont des dynamiques très différentes. Des exemples sont visibles
sur le web 2. Individuellement, chaque canal a un comportement stochastique et devrait se modéliser
par une chaîne de Markov. Par contre, une population de canaux peut se modéliser de façon
déterministe par une équation différentielle [5, chapter 3, page 155].
La variable n(t)représente la proportion de canaux K+ouverts [5, chapter 3, page 148]. La
forme des expressions αn(V)et βn(V)est suggerée par des arguments à base d’énergie libre [5,
chapter 3, pages 148-151]. Hodgkin et Huxley ont choisi de modéliser la condutance de l’ensemble
des canaux K+par un monôme
gK=gKn4
où greprésente une conductance maximale. L’exposant 4de la formule a été choisi empiriquement
[5, chapter 5, pages 203]. On peut lui donner une interprétation : chaque canal est formé de quatre
composants et n’est ouvert que si ses quatre composants le sont. Pour les canaux Na+, le principe
est le même mais en plus compliqué. La formule choisie par Hodgkin et Huxley est :
gNa =gNa m3h
Informellement, la variable mcode l’ouverture de canaux et hl’inactivation. La formule
gL=gL
modélise la conductance des fuites (leak en Anglais) et des canaux ioniques Cl−qui ne figurent pas
explicitement dans le modèle.
2. www.bem.fi/book/04/04.htm, section 4.6.4.
4

R´ ef´ erences
[1] Bruce Alberts, Alexander Johnson, Julian Lewis, Martin Raff, Keith Roberts, and Peter Walter.
Molecular Biology of the Cell. Garland Science, 5th edition, 2008.
[2] Bertil Hille. Ions Channels of Excitable Membranes. Sinauer Associates, Inc., third edition,
2001.
[3] Alan Lloyd Hodgkin and Andrew F. Huxley. A quantitative description of membrane current
and its application to conduction and excitation in nerve. J. Physiolog., 117 :500–544, 1952.
[4] Eugene M. Izhikevich. Dynamical Systems in Neuroscience. The Geometry of Excitability and
Bursting. The MIT Press, 2010.
[5] James Keener and James Sneyd. Mathematical Physiology I : Cellular Physiology, volume 8/I
of Interdisciplinary Applied Mathematics. Springer Verlag, second edition, 2010.
5