Par l`introduction d`un systme de coordonnes cylindriques selon la

Poiseuille_Tube , Licence LPA , Année 2009-2010, Daniel Huilier
(tiré du web de Ryhming, Medit , Ecole Polytechnique Fédérale de Lausanne ), http://linpc3.epfl.ch/e-lin/Ryhming/
1
Ecoulement laminaire de fluide visqueux en conduite circulaire
Equations de Navier Stokes en coordonnées cylindriques (x,r, ω = θ)
xx
xx
r
x
x
xfu
x
p
u
r
u
r
u
u
x
u
u
t
u
ρμ
ω
ρ
ω
+∇+
∂
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂2 (0.1)
r
r
r
rr
r
r
x
rf
u
rr
u
u
r
p
r
u
u
r
u
r
u
u
x
u
u
t
u
ρ
ω
μ
ω
ρωωω +
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−−∇+
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
22
2
22 (0.2)
ω
ω
ω
ωωωωωω
ρ
ω
μ
ωω
ρ f
u
rr
u
u
p
r
uuu
r
u
r
u
u
x
u
u
t
ur
r
rx +
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+−∇+
∂
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
22
22 (0.3)
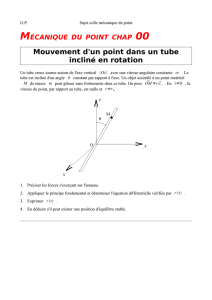
Par l'introduction d'un système de coordonnées cylindriques selon la figure ci-dessous, la vitesse
longitudinale dans le tube devient une fonction de r, u = u(r). Les équations (0.2) et (0.3)
permettent de dire que la pression ne dépend ni de r, ni de ω, donc p = p(x).
uux=
Le gradient de pression dp/dx est considéré comme constant et les équations de Navier-Stokes en
coordonnées cylindriques s'écrivent :
222
2
2
2
2
,
11 zyr
dx
dp
dr
du
r
dr
d
r
zu yu+=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
∂
∂
+
∂
∂
μ
(1)
d'où
⎟
⎠
⎞
⎜
⎝
⎛
=+=
⎟
⎠
⎞
⎜
⎝
⎛
dx
dp
dr
du
duud
r
dr
du
r
dr
d
r
μ
11
2
2
(2)
Figure: Coordonnées cylindriques x r de l'écoulement dans un tube circulaire.

Poiseuille_Tube , Licence LPA , Année 2009-2010, Daniel Huilier
(tiré du web de Ryhming, Medit , Ecole Polytechnique Fédérale de Lausanne ), http://linpc3.epfl.ch/e-lin/Ryhming/
2
En fait l’équation (2) s’écrit : ⎟
⎠
⎞
⎜
⎝
⎛
=+ dx
dp
dr
du
r
drud
μ
11
2
2
,
le membre de gauche est une fonction de r, celui de droite une fonction de x, donc chacun des
termes est constant, ce qui donne un gradient de pression constant.
Les conditions aux limites sont exprimées par u = 0 à la paroi r = a du tube et par la symétrie de la
fonction u (r) autour de l'axe r = 0. Ceci signifie que pour r → 0, on obtient selon la condition du/dr = 0.
Par intégration de (2), on obtient
r
C
r
dx
dp
dr
du 1
2
1+
⎟
⎠
⎞
⎜
⎝
⎛
=
μ
(3)
La condition de symétrie autour de r = 0 donne C1 = 0. En intégrant (3) et en tenant compte de la
condition à la limite à la paroi (r = R = a), le résultat final s'écrit
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
2
2
1
4
)( a
r
dx
dpa
ru
μ
(4)
Le profil de vitesse est donc parabolique (figure1 ci-dessous). Pour évaluer le débit-masse dans le tube, on
a besoin de la vitesse moyenne um. En se référant à la figure, on obtient
=
⎟
⎠
⎞
⎜
⎝
⎛
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−= ∫∫ a
r
d
a
r
a
r
dx
dpa
rdrru
a
aa 2
0
2
0
21
4
2)(
1
μ
π
π
= ⎟
⎠
⎞
⎜
⎝
⎛
−dx
dpa
μ 8
2
(5)
Figure 1: Profil de vitesse parabolique dans
un tube circulaire.
Figure 2: Forces de frottement et de pression
sur un volume de contrôle dans le tube
circulaire.

Poiseuille_Tube , Licence LPA , Année 2009-2010, Daniel Huilier
(tiré du web de Ryhming, Medit , Ecole Polytechnique Fédérale de Lausanne ), http://linpc3.epfl.ch/e-lin/Ryhming/
3
La distribution de vitesse peut donc s'écrire
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡⎟
⎠
⎞
⎜
⎝
⎛
−==
2
12)( a
r
uru m (6)
et la pression baisse donc le long du tube si um > 0 Selon (5), on obtient
42
8
8
aM a
u
dx
dp m&
μ
μ
−=−= ,
m
uaM ρπ
2
=
&(7)
Le débit-masse
M
&dans le tube est donc proportionnel à a4 et au gradient de pression dx
dp . La
diminution de la pression est due au frottement à la paroi du tube. Le théorème de quantité de
mouvement, appliqué au volume de contrôle de longueur dx dans la direction i selon la figure 2,
donne (attention, la contrainte > 0 est déjà orientée physiquement vers les x positifs et ce
qui agit sur le volume de contrôle est : -
p
τ
p
τ
)
02
2=−− dxadpa P
πτπ , ⎟
⎠
⎞
⎜
⎝
⎛
=dx
dp
a
P24
τ
(8)
où , la contrainte de cisaillement à la paroi, a été exprimée en fonction du diamètre 2a du
tube. Il est d'usage de définir un
p
τ
coefficient de perte de charge
λ
(ou f) par
()
Re
6432
)2/1(
4
)2/1(
2/
22 ===
−
=
m
m
P
mua
uu adxdp
ρ
μ
ρ
τ
ρ
λ
(9)
où le nombre de Reynolds est défini par rapport au diamètre 2 a et à la vitesse um. est donc
uniquement une fonction de Re. La généralisation de (9) appelée loi de Poiseuille ou Hagen-
Poiseuille pour un écoulement turbulent dans une conduite de paroi lisse ou rugueuse et de
section arbitraire est donnée ailleurs (lois de Blasius et diagrammes de Moddy-Nikuradse) .
f
ς
On peut également évaluer selon la définition. Dans ce cas il faut définir une coordonnée y
mesurée à partir de la paroi et orientée vers le centre du tube (fig. ci-dessous). Par conséquent, on
pose y = a - r et on obtient
p
τ
)()0( ar
r
u
y
y
u
P=
∂
∂
−==
∂
∂
= μμτ (10)

Poiseuille_Tube , Licence LPA , Année 2009-2010, Daniel Huilier
(tiré du web de Ryhming, Medit , Ecole Polytechnique Fédérale de Lausanne ), http://linpc3.epfl.ch/e-lin/Ryhming/
4
En utilisant (6) et (7) il vient
⎟
⎠
⎞
⎜
⎝
⎛−==
⎥
⎦
⎤
⎢
⎣
⎡⎟
⎠
⎞
⎜
⎝
⎛
−−=
=dx
dpa
a
u
a
r
um
ar
mP 2
422 2
μμτ
(11)
confirmant le résultat selon (8).
Figure: Evaluation de p
τ
d'après la formule
(10).
Généralisation des perte de charges régulières (linéaires) dans les conduites
Rappels théoriques
Equation de Darcy-Weisbach (1854,1845) :Loi générale de la perte de charge Δh , Δp est
gD
LU
h2. .
2
λ =Δ , D
LU
hgp .2 .
2
ρ
λρ
=Δ=Δ
avec :
λ : coefficient de perte de charge
U : vitesse moyenne de débit (=Q/S)
Q : débit volumique,
S : section de la conduite,
D : diamètre de la conduite,
L : longueur du tronçon de la conduite,
λ est fonction du nombre de Reynolds
- pour Re < 2400, régime de Poiseuille : λ = 64.Re-1
- pour Re > 2400, régime de Blasius : λ =0.3164.Re-1/4
Nombre de Reynolds Re = U.D/ν avec ν : viscosité cinématique du fluide

Poiseuille_Tube , Licence LPA , Année 2009-2010, Daniel Huilier
(tiré du web de Ryhming, Medit , Ecole Polytechnique Fédérale de Lausanne ), http://linpc3.epfl.ch/e-lin/Ryhming/
5