ra va il et é ne rgie - Fabrice CAPBERT

Chapitre : « ravail et énergie »
1
5 personnes tirent un wagon vers la droite, complétez le
schéma :
A- Je fais ce que je peux !
B- Je ne sers à rien !
C- C'est moi le meilleur !
D- Je résisterai !
De quoi dépend, l’éfficacité de la force exercée par chaque
personne dans la mise en mouvement du chariot.
……………………………………………………………………………………………………
……………………………………………………………………………………………………
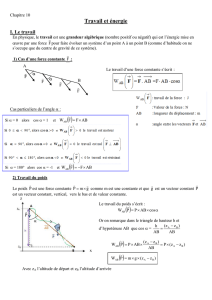
I Travail d’une force constante:
1- Expression mathématique :
Une condition nécessaire pour qu’une force travail est que son point d’application se déplace.
Soit une force
F
constante appliquée entre les points A et B. Le travail de cette force entre le point
A et B, notée WAB
)F(
est égal au ……………………………… du vecteur déplacement par le vecteur force
WAB (
F
) en joule (…), F en Newton(…), AB en mètre (…).
2- Travail moteur et résistant :
Lorsque le système reçoit du travail d'une
force extérieure, alors ce travail est
positif, il s'agit d'un travail moteur.
Lorsque le système fournit du travail au
milieu extérieur alors le travail est
négatif, il s'agit d'un travail résistant.
Lycée Joliot Curie à 7
PHYSIQUE
Classe de Ter S
Thème : Comprendre
Cours « Travail et énergie »
α
valeur du travail
travail moteur ou
résistant?
α
=0
WAB =
travail …………………
2
π
α0
WAB =
travail …………………
2
π
α
WAB =
travail …………………
πα
2
π
WAB =
travail …………………

Chapitre : « ravail et énergie »
2
3- Force conservatrice
Une force est dite conservative si son
travail entre deux points A et B quelconques
……………………………………… de la trajectoire suivie
entre ces deux points.
Toutes les forces constantes sont
conservatives : le poids (dans un champ de
pesanteur uniforme), la force électrique
(dans un champ électrostatique uniforme),
mais aussi d’autres forces non constantes
(force de rappel élastique d’un ressort, par
exemple).
Remarque :
Les forces de frottements ou la force de tension d’un fil sont des forces
non-conservatives.
II Travaux de quelques forces :
1- Travail du poids dans un champ de pesanteur uniforme
Soit un objet de masse m qui parcourt un déplacement quelconque
entre deux points A et B dans un champ de pesanteur uniforme g
Le poids exercé sur cet objet est une force constante, P=mg
Le travail du poids a pour expression
Dans le repère (O, , ,  ), associé au référentiel terrestre, si l’axe
(Oz) est un axe vertical ascendant,
Exemple : calculer le travail du poids du ballon de basket (m = 650 g) entre le point de lancer
(altitude : 2,20 m) et le panier (altitude : 3,05 m). Commenter le signe de ce résultat.
W = – 5,42 J.

Chapitre : « ravail et énergie »
3
Soit un objet de masse m se déplaçant d'un point A d'altitude zA à un point B d'altitude zB dans un référentiel
galiléen. Le travail du poids est égal à:
Unité: WAB (
P
) en joule (J), m (kg), g (N.kg-1), zA et zB en mètre (m)
Le travail du poids ne dépend pas du chemin suivi mais uniquement de l'altitude initiale et de l'altitude
finale: on dit que le poids est une force ………………………………………….
2-Travail de la force électrique en champ électrostatique uniforme
Entre deux plaques P et N d’un condensateur plan règne un champ
électrostatique uniforme E perpendiculaire aux plaques. Une particule
de charge q en mouvement entre les deux plaques est soumise à la
force électrique  =q
.
Entre deux points A et B, la force électrique est constante,
donc conservative et son travail sur le trajet AB ne dépend pas du
chemin suivi. Il peut donc être calculé en passant par le point C,
Exercice : L’électron-volt, de symbole eV, est une unité d’énergie égale à la valeur absolue du travail de la
force électrique exercée sur un électron lors d’un déplacement correspondant à une tension de 1 V. Calculer la
valeur d’un électron-volt en joules.
Réponse : 1 eV = e J = 1,60218.10−19J
3- Travail d’une force de frottements d’intensité constante sur une trajectoire rectiligne
Une force de frottements  n’est pas conservative. Ainsi, le travail de cette force sur un déplacement allant
de A vers B dépend du chemin emprunté : plus il est long, plus le système perd de l’énergie par transfert
thermique vers l’extérieur, assuré par le travail de la force de frottements.
Sur une trajectoire rectiligne, une force de frottements d’intensité constante a même direction
(celle du déplacement) et même sens (opposé au déplacement) à chaque instant. Il vient
Ce travail est négatif : il réalise un transfert thermique vers ………………………………….
III- Energies et travaux des forces conservatives :
1- Variation d'énergie potentielle de pesanteur Epp et travail du poids :
Considérons une altitude de référence zo = 0
m. Un solide de masse 'm' placé dans le
champ de pesanteur terrestre 'g' à une
altitude 'z' possède une énergie potentielle
de pesanteur:
Unité: Epp(J), m (kg), z(m).

Chapitre : « ravail et énergie »
4
La variation d'énergie potentielle d'un objet de masse m se déplaçant d'un point A d'altitude zA à un
point B d'altitude zB est:
On a vu que le travail du poids d’un objet de masse m se déplaçant d'un point A d'altitude zA à un point B
d'altitude zB dans un référentiel galiléen était:
il vient
…………………………………………………………………………………………………………………………………………………………………………………
2-Variation d'énergie potentielle électrique et travail de la force électrostatique
a- énergie potentielle électrique Epe
L'énergie potentielle électrique d'une charge q
dont le potentiel électrique est V est:
Unité: Epe (…), q(…), V(…)
b- variation d'énergie potentielle électrique et
travail de la force électrique
La variation d'énergie potentielle électrique entre
le point A de potentiel VA et le point B, de
potentiel VB est:
Or le travail de la force conservative électrostatique entre le point A et le point B est:
Par conséquent le travail de la force conservative électrique est égale à l'opposé à la variation de l'énergie
potentielle électrique:
Généralisation: la variation d'énergie potentielle d'un système se déplaçant d'un point A à un point B
est égale à l'opposé de la somme des travaux effectués par les forces conservatives entre le point A
et le point B:
3- l'énergie mécanique: cas du mouvement dans frottement
a- théorème de l'énergie cinétique
Le théorème de l'énergie cinétique nous dit que la variation de l'énergie cinétique d'un système de
masse m entre un point A et un point B est égale à la somme du travail des forces non conservatives
(Fnc) et du travail des forces conservatives (Fc):
)
c
F(
AB
W)
nc
F(
AB
W
BA
Ec

Chapitre : « ravail et énergie »
5
b- conservation de l'énergie mécanique
Rappel:
- l'énergie mécanique d'un système de masse m, se déplaçant à une vitesse v dans un champ de
pesanteur uniforme g est:
- la variation d'énergie potentielle de pesanteur entre les points A et B est:
Lorsqu'un système en mouvement n'est soumis à aucune force de frottement (force non
conservative) la variation d'énergie mécanique est nulle au cours du temps. L'énergie mécanique se
conserve. En effet:
L'énergie cinétique se transforme en énergie potentielle de pesanteur et inversement au cours du mouvement.
http://physiquecollege.free.fr/lycee_premiere.htm