Algorithme

Algo
Algorithme
Chapitre 1 : du problème au programme en
passant par l'algorithme
I. Introduction
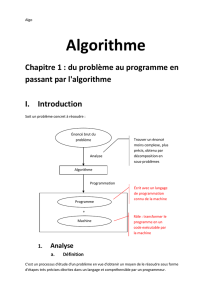
Soit un problème concret à résoudre :
1. Analyse
a. Définition
C'est un processus d'étude d'un problème en vue d'obtenir un moyen de le résoudre sous forme
d'étapes très précises décrites dans un langage et compréhensible par un programmeur.
Énoncé brut du
problème
Algorithme
+
Programme
Machine
Analyse
Programmation
Trouver un énoncé
moins complexe, plus
précis, obtenu par
décomposition en
sous-problèmes
Écrit avec un langage
de programmation
connu de la machine
Rôle : transformer le
programme en un
code exécutable par
la machine

Algo
On obtient de ce fait un algorithme.
Problème : une tâche à résoudre
La phase d'analyse contient une étape préliminaire appelée pré-étude : elle permet d'identifier le
résultat souhaité et les données (informations) qui conçurent à) l'obtenir.
Exemple : gestion simplifiée d'une facture téléphonique :
 Résultat : montant à payer
 Données : montant abonnement, prix unité, nombre d'unités consommées.
b. Forme d'analyse
Il existe 2 formes d'analyse :
 L'analyse guidée par le(s) résultat(s)
Résultat(s) --> donnée(s)
Décomposition :
L'analyse par le résultat correspond à une décomposition d'un problème en sous-problèmes
moins complexes à résoudre et ainsi de suite pour chaque sous-problème jusqu'à arriver aux
données.
 L'analyse guidée par la(les) donnée(s)
Résultat
Résultat 1
Résultat 2
Résultat 3
Résultat 4
Résultat a
Résultat b
Résultat n
...
...
...
- - - - - - -
- - - - - - -
- - - - - - -
Donnée 1
Donnée 2
Donnée P
Résultat
Résultat 1
Résultat 2
Résultat n
Donnée 1
Donnée 2
Donnée P

Algo
2. Notion d'algorithme
Définition d'un algorithme (d'après D.E. Knuth, une des personnes de l'informatique de l'Université
de Stanford, 1968, ;1973. Il a donné une liste de 5 propriétés largement reconnues comme pré-
requises d'un algorithme) :
1) Finitude : un algorithme doit toujours se terminer après un nombre fini d'étapes.
2) Définition précise : chaque étape d'un algorithme doit être défini de manière très précise,
les actions doivent être très bien spécifiées et être sans ambiguïtés pour chaque cas
3) Entrées : ce sont des quantités (informatiques) données ) l'algorithme avant qu'l ne
commence
4) Sortes : ce sont des quantités (informatiques) qui ont une relation spécifique avec les
entrées
5) Rendement : toutes les opérations qu'il doit accomplir doivent être suffisamment basiques
pour être réalisée dans une durée finie par un homme utilisant du papier et un crayon.
En d'autres termes, un algorithme est un ensemble de règles ayant les caractéristiques suivantes :
 Il doit être fini et terminé après un nombre fini d'opérations
 Il doit être défini et précis : chaque opération est spécifiée sans ambiguïtés
 Les champs d'application des données sont précisées sans ambiguïtés
 Il doit être effectif : toutes les opérations doivent pouvoir être faites par l'utilisateur.
II. Algorithme et méthode
1. Syntaxe
Un algorithme sera composé de 3 parties :
 Instructions : les différentes étapes de résolution
 Ordonnancement : indique l'ordre selon lequel doivent se dérouler les différentes étapes
 Lexique : identifie les différents objets (données ou résultats) manipulées
Un algorithme est identifié par un nom
Forme :
Algo nomAlgo
Ord
Lexique
Définitions (ou instructions)
Numéro
d'ordre
Les objets
Deux types d'analyse <==> deux types d'algorithmes,

Algo
2. Exemple : facture téléphonique
Résultat : montant à payer
Données : montant de l'abonnement, prix de l'unité, nombre d'unités consommées
a. Analyse par résultat
Algo Facture
Ord
Lexique
Résultat : montant à payer
montantPaye = montantAbonnement +
prixConso
prixConso = nombreUnite * prixUnite
Données : montantAbonnement, prixUnite,
nombreUnite
4
3
2
1
montantPaye (réel)
prixConso (réel)
nombreUnite (entier)
prixUnite (réel)
montantAbonnement (réel)
b. Analyse par données
Algo Facture
Ord
Lexique
Données : montantAbonnement, prixUnite,
nombreUnite
prixConso = nombreUnite * prixUnite
montantPaye = montantAbonnement +
prixConso
Résultat : montant à payer
1
2
3
4
montantPaye (réel)
prixConso (réel)
nombreUnite (entier)
prixUnite (réel)
montantAbonnement (réel)
3. Notion de variable
Définition : une variable est un nom qui permet d'identifier un objet manipulé dans un algorithme.
L'objet possède une valeur qui peut changer dans le temps dans l'algorithme qui l'utilise.
Schématisation : on peut représenter à l'aide d'une boîte (qui correspond à un moment de la
programmation à l'emplacement mémoire de l'ordi).
(contenu qui correspond à la valeur
de l'objet)
Contenu

Algo
4. Une première instruction : l'affectation
Définition : c'est l'instruction qui permet d'associer une valeur à une variable. La valeur peut être une
valeur constante, ou une valeur calculée.
Symbole utilisé : <--
Utilisation : nomVariable <-- valeur
Sens : La variable prend la valeur X
Ou : la valeur X est affectée à la variable
Nom d'une variable : chaîne de caractère alphanumérique.
Exemples :
prixConso, a, AB_40, xy, prix_Unite, montant_abonnement, titi, etc...
PrixConso <-- nombreUnite * prixUnite
Remarque : dans un lexique, définir a comme variable ne signifie pas que a contient une valeur.
Notion de constante : On peut associer un nom à une valeur constante et manipuler cette valeur
uniquement à travers son nom dans l'algorithme.
Exemple : On peut associer le nom pi à la valeur 3.14
5. Notion de type
La forme du contenu d'une variable est définie par le concept du type.
À toute variable est associé un type.
Les types permettent de définir :
 L'ensemble des valeurs que pourra prendre la variable (domaine de définition)
 L'ensemble des opérations applicables à la variable
 La forme des représentations (ou "codage") en mémoire d'ordinateur
Les types simples :
 Entiers
 Réels
 Caractère
 Chaîne