Atelier algorithmique et éléments de correction

ATELIER ALGORITHMIQUE
Exercice d'introduction
Un problème de recherche du nombre de boites nécessaire à la confection d’une tour « chamboule-tout »
à N étages nous conduit à calculer la somme des entiers consécutifs jusqu'à un N donné.
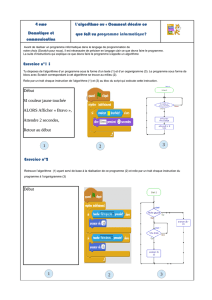
Construire un algorithme qui permet de calculer la somme des entiers consécutifs jusqu'à un N donné.
Problème des cars de supporters
Une entreprise de transport possède 4 cars de 50 places chacun et se propose d'assurer le transport des
supporters d’une équipe de rugby. Chaque car se loue 800 € tout compris.
1. Comment donner de façon automatique le prix par supporter en fonction du nombre de supporters se
rendant au stade.
2. Représenter graphiquement le prix par supporter en fonction du nombre de supporters se rendant au
stade.
3. Combien l'organisateur peut-il accepter de supporters, s'il s'est engagé à ce que le prix d'une place ne
dépasse pas 20 € ?
Exercices complémentaires
Exercice 1
Construire un algorithme donnant par balayage les minimum et maximum de la fonction f définie sur
l'intervalle
[
]
2;1
− par
(
)
3 2
3 1
f x x x x
= + − −
.
Exercice 2
Construire un algorithme permettant d'arrondir au centième près un nombre donné.
Structure SI … ALORS … SINON
Exercice 3
On tire de façon aléatoire, deux nombres x et y, compris entre
0 et 1 et on place dans le plan (rapporté à un repère
orthonormal) le point M de coordonnées (x ; y).
On effectue un grand nombre de tirages.
Faire apparaître la fréquence des points dont la distance à
l'origine est strictement inférieure à 1. Comparer cette
fréquence à
4
π
.
Remarque : Cette méthode est proche de celle des aiguilles de
Buffon pour déterminer expérimentalement une valeur de π. Il
faut faire un grand nombre de tirages car elle converge
lentement. On utilise des méthodes probabilistes, appelées
aussi méthode de Monte-Carlo, en calcul intégral pour
approcher des surfaces et des volumes.
Exercice 4
Déterminer le nombre de triangles dans cette figure.

ÉLÉMENTS DE CORRECTION
Exercice d'introduction
Problème des cars de supporters
Les exemples ci dessous donne des algorithmes ayant des différences de stratégies et des variations suivant
le langage choisi. Toutes les stratégies exposées peut être exploitées avec tous les langages.
Question 1
Avec Scratch

Exemple sous AlgoBox avec TANT QUE.
Sur calculatrices
Programme sur Graph 35 avec TANT QUE Programme sur TI avec SI…ALORS…SINON

Question 2
Voici un scénario en quatre étapes (on modifie, perfectionne l'algorithme pour passer d'une étape à l'autre…)
a. Travail par disjonction (Quatre intervalles à envisager).
(On ne teste pas ici si N est un entier pour ne pas surcharger le programme).
Ceci pourrait sembler fastidieux à taper, mais cela se fait
rapidement en utilisant la fonction "Dupliquer" de Scratch.
On tape en détail une structure "Si" que l'on duplique
ensuite.
b. Des structures conditionnelles (alternatives) emboitées.
On observe le gain en nombre de tests !
Cette étape se construit naturellement à partir de la précédente
: toute la puissance de Scratch s'exprime alors (on récupère
une partie des structures précédentes, en déplaçant les blocs).

c. Une première tentative de tracé (problème de "bavures" : ce n'est pas une fonction !)
Utilisation d'une boucle : RÉPÉTER…
Ici aussi, il suffit d'intégrer la structure précédente dans un " Répéter jusqu'à…
d. Finalisation : on relève le stylet …et on travaille sur la notion de fonction et de courbe !