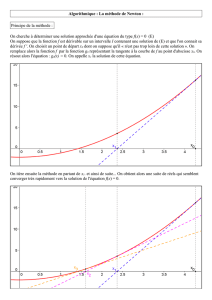
Chapitre 3

98 CHAPITRE 2. PRÉLIMINAIRES

Chapitre 3
Optimisation locale de fonctions différentiables
sans contrainte
Sujets du chapitre
‚Analyse des conditions d’optimalité (équations ou inéquations satisfaites pour
toute solution du problème d’optimisation).
‚Déduction d’une famille d’algorithmes itératifs globalement convergents à partir
de la violation des conditions d’optimalité.
‚Présentation de l’algorithme de Newton modifié.
‚Algorithmes spécialisés aux fonctions quadratiques.
‚Problèmes de moindres carrés.
‚Problèmes de très grandes dimensions.
99

100 CHAPITRE 3. OPTIMISATION DIFFÉRENTIABLES SANS CONTRAINTE
Introduction
Les problèmes d’optimisation les plus simples sont ceux qui consistent à minimiser (ou
maximiser) une fonction f:RnÑRoù la fonction fest supposée définie dans Rnen entier,
et de plus de classe C3pRnq. En fait, on suppose que fest suffisamment différentiable pour
éviter les difficultés dans l’analyse des algorithmes de solution. De plus, seuls les minima
locaux retiennent notre attention dans ce premier contact.
Les vecteurs de Rnsont des vecteurs colonnes. Les gradients des fonctions f:RnÑR,
notés ∇fpxqsont des vecteurs lignes. Une motivation pour cette notation est que le gradient
est en fait une application linéaire de Rndans Rn, donc située dans le dual de Rn. Bien que
les espaces euclidiens soient auto-duaux, il est commode de considérer le dual comme un
espace de vecteurs lignes.
La classe de tels problèmes (aussi appelés programmes non-linéaires) peut sembler trop
simple pour être vraiment utile et/ou intéressante à étudier. Cependant, l’étude de cette
classe de problèmes permet d’introduire les notions fondamentales qui seront utilisées constam-
ment dans l’étude de problèmes plus généraux, comme par exemple les problèmes où la
fonction fn’est plus assez différentiable pour permettre une analyse simple telle que nous
présentons dans ce chapitre, ou encore la classe de problèmes de minimisation d’une fonction
dans un domaine restreint de Rn.
Comme dans les chapitres suivants, nous analysons d’abord les équations et inéquations
nommées conditions d’optimalité qui caractérisent une solution au problème étudié, et ensuite
nous déduisons des algorithmes itératifs à partir de la non-réalisation de ces conditions
d’optimalité.
3.1 Formulation du problème
Énonçons le problème que nous résolvons dans ce chapitre. Il consiste à trouver un point
x˚qui minimise la fonction fdans Rn:
fpx˚q “ min
xPRnfpxq,
ou encore trouver x˚tel que
fpx˚qďfpxq,@xPRn.
Comme nous l’avons expliqué au chapitre précédent, nous nous limitons à une version locale
de ce problème, soit qu’il existe un voisinage Vpx˚qde x˚tel que
fpx˚qďfpxq,@xPVpx˚q.
Puisque la notion de voisinage entre de manière très intime dans la définition du problème,
on doit s’attendre à ce que la notion de proximité soit utilisée dans l’analyse de sa solution.

3.2. CONDITIONS D’OPTIMALITÉ 101
En général, l’analyse du problème de minimiser localement une fonction de nvariables ne
peut pas se réduire à l’analyse de la minimisation locale d’une fonction d’une seule variable.
On pourrait récrire le problème ainsi :
fpx˚qďfpx˚`dq,@dPVp0q,
où dreprésente le déplacement de x˚à un point voisin, ou encore, en séparant la notion de
direction et la notion de distance du déplacement,
fpx˚qďfpx˚`θdq,@dPRn,}d} “ 1,et @θă,
où représente le diamètre d’une boule centrée en x˚contenue dans Vpx˚q. Cependant, nous
ne pouvons pas établir d’équivalence entre les restrictions unidimensionnelles et les problèmes
originaux.
En fait, si x˚est un minimum local de f, alors 0 est un minimum local de la fonction
d’une seule variable hx˚,dpθqdef
“fpx˚`θdq, et ce quelle que soit la valeur de dPRntelle que
}d}“1. Cependant, la contraposée n’est pas vraie, comme l’illustre le programme suivant
(voir figure 3.2 et l’exercice 3.2.6) :
minpx2´yqpx2´4yq,
pour lequel l’origine est un point stationnaire correspondant à un point de selle. Pourtant,
le long de toute droite passant par l’origine, cette fonction possède un minimum local à
l’origine !
3.2 Conditions d’optimalité
Comme nous venons de le voir, en général, l’analyse du problème de minimiser localement
une fonction de nvariables ne peut pas se réduire à l’analyse de la minimisation locale d’une
fonction d’une seule variable. Malheureusement, dans la pratique, il est très difficile de traiter
systématiquement des exemples comme la fonction px2´yqpx2´4yq, et on se contente souvent
de caractérisations issues de l’analyse de la fonction univariée hx˚,d.
3.2.1 Analyse du problème à une seule variable
Penchons-nous sur le problème de minimiser une fonction réelle hpθq. Supposons sans
perte de généralité que nous étudions un minimum local de hsitué en θ“0. Exprimons h
en série de Taylor autour de θ“0 :
hpθq“hp0q ` h1p0qθ`h2p0qθ2
2! `h3p0qθ3 3! `. . . `hpjqp0qθj j!`. . .

102 CHAPITRE 3. OPTIMISATION DIFFÉRENTIABLES SANS CONTRAINTE
Supposons maintenant que les j´1 premières dérivées de hau point 0 sont toutes nulles, et
que la première non-nulle est hpjqp0q. Alors, en utilisant le théorème de Taylor, on a
hpθq“hp0q ` hpjqp0qθj
j!`Rj`1pθq,
où Rj`1pθqest le reste d’ordre j`1. On voit donc que 0 est un minimum local si hpjqp0qθj
j!`
Rj`1pθqest positif pour des valeurs suffisamment petites de |θ|. Détaillons ce raisonnement.
Maintenant, toujours supposant que hest suffisamment (j`1 fois) différentiable, le reste
Rj`1pθqsatisfait à la borne
DK1:|Rj`1pθq| ďK1|θj`1|.
Plus précisément, rappelons que lorsque les fonctions sont suffisamment différentiables, le
reste s’écrit
Rj`1pθq “ hpj`1qpξqθj`1
pj`1q!,
où comme à l’accoutumée, ξ“αθ avec 0 ďαď1. Puisque hest suffisamment différentiable,
hpj`1qest une fonction continue, et donc, bornée ; en fait, quelle que soit la borne que l’on
ait en tête de la forme |hpj`1qp0q|`δ, il existe un δą0 tel que si |ξ|ă, alors |hpj`1qpξq| ă
|hpj`1qp0q| ` δ. En d’autres termes, si une fonction φest continue à l’origine, alors, pas trop
loin de l’origine, φpξqne sera pas beaucoup plus grand que φp0q. Supposons donc maintenant
δ“1 de sorte que si |ξ|ă1, on a la garantie que |hpj`1qpξq| ă|hpj`1qp0q|`1. Donc, on peut
prendre K1“1
pj`1q!p|hpj`1qp0q| ` 1q.
Intéressons-nous maintenant au signe de la quantité hpjqp0qθj
j!`Rj`1pθqqui peut se récrire
θj
j!ˆhpjqp0q ` hpj`1qpξqθ pj`1q˙.p1q
Puisque nous avons fait l’hypothèse que les j´1 premières dérivées de hétaient nulles et
que la jième est non-nulle, vérifions que le signe de phpjqp0q` hpj`1qpξqθ
pj`1qqest donné par le signe
de hpjqp0qlorsque θest assez petit, et précisons ce que nous entendons par assez petit.
Pour ce faire, argumentons que si hpjqp0qdomine hpj`1qpξqθ
pj`1qen valeur absolue, ce dernier
terme ne peut pas faire changer le signe de la somme, donné par le signe du premier terme.
Écrivons donc
|hpjqp0q| ąˇˇˇˇ
hpj`1qpξqθ
pj`1qˇˇˇˇ“ˇˇˇˇ
hpj`1qpξq
pj`1qˇˇˇˇ|θ|.
Donc, si
|θ|ăpj`1q|hpjqp0q|
|hpj`1qpξq| ,