résonance, filtrage d`une tension créneau

filtrage d'une tension non sinusoïdale par un circuit RLC
1. réponse du circuit en régime sinusoïdal :
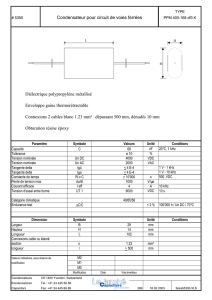
on considère le circuit RLC ci-contre, avec :
L = 2,50 mH (bobine parfaite, Rbobine = 0)
R = 100 Ω
C = 100 nF
il est alimenté par un générateur BF sinusoïdal parfait
(R
géné
= 0) de tension efficace VE ;
on mesure la tension efficace VS aux bornes de R, et on
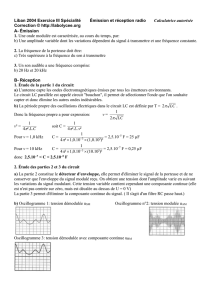
trace VS/VE en fonction de la fréquence f :
1.1 retrouver la fréquence de résonance f
0
du circuit, à partir des valeurs des composants.
1.2 déterminer à partir du graphe, la bande passante f
2
- f
1
du circuit.
1.3 en déduire le facteur de qualité Q
0
et le coefficient d'amortissement σ.
1.4 vérifier ces résultats à partir des valeurs des composants.
2. filtrage d'une tension créneau
on alimente maintenant ce circuit par une tension créneau, de fréquence 5,00 kHz, de valeur moyenne nulle, de
rapport cyclique égal à 1, dont la décomposition en série de Fourier donne pour l'harmonique de rang n :
U
n
= 4U/nπ avec n impair, et U = 5,00 V
2.1 déterminer à partir du graphe, les valeurs maximales des harmoniques de rangs 1, 3, 5 et 7 de la tension de
sortie VS.
2.2 en se limitant à ces quatre harmoniques, calculer la valeur efficace de la tension de sortie VS.
2.3 avec la même inductance, calculer la valeur de la capacité et de la résistance permettant de "sélectionner" la
fréquence f = 20 kHz avec un facteur de qualité supérieur à 10.
_____________________
Frequency
0Hz 5KHz 10KHz 15KHz 20KHz 25KHz 30KHz 35KHz 40KHz
V(VS)/ V(VE)
0
0.5
1.0

corrigé : filtrage d'une tension non sinusoïdale par un circuit RLC
1. réponse du circuit en régime sinusoïdal
1.1sur le graphe, on lit la fréquence de résonance f
0
du circuit : 10 kHz ;
à partir des valeurs des composants on aurait f
0
= ω
0
/2π = =
π
=
π
−9
10.100.0025,02
1
LC2
1
10,0 kHz
c'est bien en accord avec la valeur précédente.
1.2 on lit également sur le graphe : f
1
= 7,4 kHz, f
2
= 13,7 kHz (lecture ± 0,1 kHz) pour H = H
max
/√2 = 0,707
la bande passante f
2
- f
1
est donc 13,7 - 7,4 = 6,3 kHz (± 0,2kHz)
1.3 Q
0
= 6,1
3,6
10
ff
f
12
0
12
0
==
−
=
ω−ω ω
et
σ
=2
1
Q
0
donne σ = 0,31
1.4 à partir des expressions
LC
1
0
=ω et
L
C
2
R
=σ il vient :
R
L
LC
L
R
1
C
L
R
1
2
1
Q
0
2
0
ω
===
σ
=
soit ici : =
π
=
ω
=100 10.2.0025,0
R
L
Q
4
0
0
1,57 ≈ 1,6 on retrouve bien la même valeur.
2. filtrage d'une tension créneau :
2.1 un générateur de tension créneau est équivalent à un ensemble de générateurs sinusoïdaux correspondant à
chaque harmonique, placés en série; en appliquant le théorême de superposition, on peut écrire pour
l'harmonique de rang n aux bornes de la résistance :
nn
VE
)
Cn
1
Ln(jR
R
VS
ω
−ω+
=
et sa valeur maximale
n
22
n
VE
)
Cn
1
Ln(R
R
VS
ω
−ω+
=
avec VE
n
= 4U/nπ
puis la valeur maximale de la tension de sortie non sinusoïdale : ...VVVV
2
5s
2
3s
2
1sS
+++=
Frequency
0Hz 5KHz 10KHz 15KHz 20KHz 25KHz 30KHz 35KHz 40KHz
V(VS)/ V(VE)
0
0.5
1.0
H
max
/
√
2 = 0,707
f
1
= 7,4 kHz
f
2
= 13,7 kHz

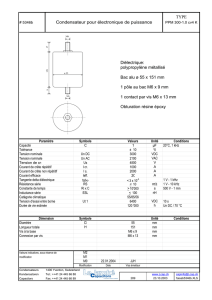
à partir du graphe on peut déterminer les valeurs du module de la fonction de transfert pour l'harmonique de rang
n, puis la valeur de VS
n
= H
n
VE
n
= H
n
4U/nπ (valeurs maximales) avec U = 5,0 V:
rang n 1 3 5 7
fréquence (kHz) 5,00 15,0 25,0 35,0
VE
n
=4U/nπ 6,37 2,12 1,27 0,91
H
n
± 0,01 0,38 0,61 0,29 0,19
VS
n
= H
n
VE
n
2,45 1,30 0.37 0,18
(valeurs maximales)
2.2 en se limitant à ces quatre harmoniques, on calcule la valeur maxi. de VS:
2
7
2
5
2
3
2
1
VSVSVSVSVS +++= = =+++
2222
18,037,030,145,2 2,80 V VS = 2,80 V et VS
eff
= 1,98 V
2.3 pour "sélectionner" la fréquence 20 kHz (d'un autre signal), il faudrait avoir f
0
= 20 kHz
or f
0
= ω
0
/2π =
LC2
1
π
ce qui donne : =
π
=Lf4
1
C
2
0
2
25,3 nF
le facteur de qualité est lié à la résistance par
R
L
Q
0
0
ω
= et on veut Q
0
> 10 d'où =
π
<10 20000..2.0025,0 R 31,4 Ω
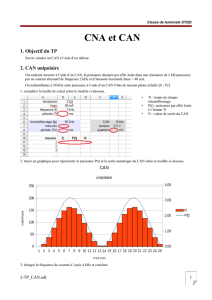
on obtiendrait alors la courbe de résonnce suivante :
Frequency
0Hz 5KHz 10KHz 15KHz 20KHz 25KHz 30KHz 35KHz 40KHz
V(VS)/ V(VE)
0
0.5
1.0
________________________
Frequency
0Hz 5KHz 10KHz 15KHz 20KHz 25KHz 30KHz 35KHz 40KHz
V(VS)/ V(VE)
0
0.5
1.0
H
1
H
3
H
5
H
7