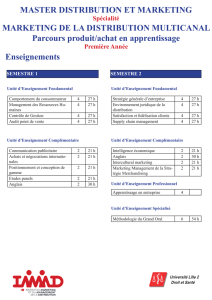
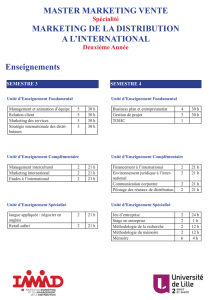
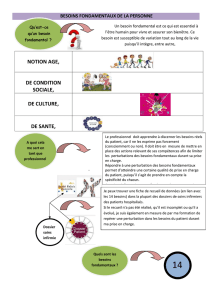
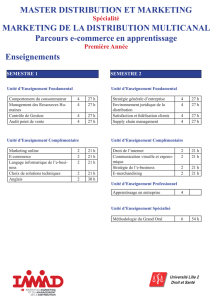
Méthode des variations

H
H
H|uni=En|uni
n= 0,1,2, ...
E0≤E1≤E2...
|ψi
H
|ψi=X
n
cn|uni

cn=hun|ψi|ψi
hEi=hψ|H|ψi
hψ|ψi
=(Pmc∗
mhum|)H(Pncn|uni)
(Pmhum|c∗
m) (Pncn|uni)
=Pm,n c∗
mcnEnhum|uni
Pm,n c∗
mcnEnhum|uni
hum|uni=δm,n
hEi=Pn|cn|2En
Pn|cn|
hEi=hψ|H|ψi
hψ|ψi≥E0
H|ψi
|ψiH E0
αi
ψt=ψt(α1, α2, ..., αs)
E(α1, ..., αs) = hψt|H|ψti
hψt|ψti
αi
∂E (α1, ..., αs)
∂αi
= 0 , i = 1, ..., s
E(α1, ..., αs)

l= 0
s
r ψ (r= 0) 6= 0
ψt(r) = Ce−αr
α C
hψt|ψti=|C|2ˆ∞
0
e−2αr4πr2dr = 1
|C|=rα3
π
H=T+V=−~2
2m∇2−e2 4πε0r
hψt|T|ψti hψt|V|ψti
hψt|−e2
4πε0
1
r|ψti=−e2 4πε0ˆ∞
0
ψ∗
t(r)1
rψt(r) 4πr2dr
=−e2
4πε0
α

∇.(U∇V) = U∇2V+∇U.∇V
U V ψ∗ψ
ˆ∇.(ψ∗∇ψ)d3r=ˆψ∗∇2ψd3r+ˆ∇ψ∗.∇ψd3r
A
ˆτ
∇.Adτ =ˆS A·dS
ˆ∇.(ψ∗∇ψ)dτ =ˆS
(ψ∗∇ψ)dS
r→0ˆψ∗∇2ψd3r=ˆ|∇ψ|2d3r
|∇ψ|2∇2ψ
hψt|−~2
2m∇2|ψti=−h2 2mˆψ∗
t∇2ψtd3r=~2
2mˆ|∇ψt|2d3r
|∇ψt|2=
∂ψt
∂r 
2
=α2|ψt|2
hψt|−~2
2m∇2|ψti=~2α2 2m
E(α) = hψt|H|ψti=~2α2
2m−e2α 4πε0
E(α)
∂E (α)
∂α α0
= 0

α0=me2
4πε0~2
α0α0= 1/a0
E(α0)
E(α0) = ~2
2ma2
0−e2
4πε0a0
~2/ma0=e2/4πε0
E1
a0== −1 2e2 4πε0a0=−13.6
ψt(x) = Ce−αx2
V(x) = −βδ (x)
β > 0
a > 0n= 0,1,2,
ˆ∞
0
dx xne−ax =n!
an+1
ˆ∞
0
dx xne−ax2=Γn+1
2
2a(n+1)
2
Γ1
2=√πΓ3 2=√π 2Γ5 2=3√π 4