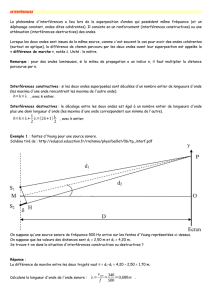
[2] Interférences à deux ondes

Optique Ondulatoire
Plan du cours
[1] Aspect ondulatoire de la lumière
[2] Interférences à deux ondes
[3] Division du front d’onde
[4] Division d’amplitude
[5] Polarisation
[6] Diffraction
[7] Interférences à ondes multiples
1
Chapitre 2 – Interférences à deux ondes
1 – Position du problème
Nous allons traiter ici le cas de deux ondes électromagnétiques
monochromatiques de pulsations
ω
1et
ω
2issues de deux sources ponctuelles
S1et S2.
Quelle est la valeur de l’intensité I au point M ?
?
Milieu homogène d’indice n
×
2

Chapitre 2 – Interférences à deux ondes
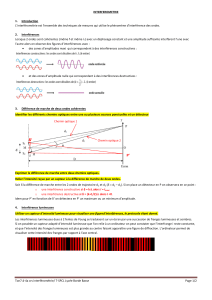
Illustration : interférences de deux ondes scalaires parfaitement cohérentes : ω
1=
ω
2.
0
>
0
=
0
<
Représentation en fausses
couleurs de :
2 – Simulations numériques
M
:
:
×
S1S2
3
Chapitre 2 – Interférences à deux ondes
Fixons maintenant l’instant d ’observation t0:
4

Chapitre 2 – Interférences à deux ondes
- Amplitude complexe de l’onde issue de S2:
- Amplitude complexe de l’onde issue de S1:
Au point Mle champ électromagnétique complexe s’écrit :
L’intensité totale Iau point Ms’écrit alors :
3 – Calcul de l ’intensité
5
Dans le cas générale l’intensité due aux deux ondes au point Mn’est pas
simplement la somme des intensités des deux ondes incidentes.
Le terme supplémentaire est le terme d’interférence.
Chapitre 2 – Interférences à deux ondes
Notons : et : les intensités des ondes incidentes
On obtient alors :
En utilisant les formules d’EULER :
6

4 – Obtention des interférences
Chapitre 2 – Interférences à deux ondes
Dans l’expression du terme d’interférence subsiste un terme dépendant du
temps.
A priori l’échelle de temps de variation des phases et est plus
petite que le temps de réponse du détecteur.
Il faut donc remplacer le terme dépendant du temps par sa valeur moyenne
temporelle :
4.1) Remarque préliminaire
7
Chapitre 2 – Interférences à deux ondes
4.2) Conditions d’observation des interférences
Condition sur la polarisation de la lumière :
Les champs interférant doivent être parallèles.
Si les ondes sont polarisées orthogonalement : et il n’y a pas
d’interférences.
Interférences non visibles Interférences les plus
contrastées 8

Chapitre 2 – Interférences à deux ondes
Condition sur la fréquence des ondes lumineuses
La différence de phase s’écrit :
Si les pulsations ω
1et
ω
2sont différentes le terme (
ω
1−
ω
2)tvarie rapidement
dans le temps et la valeur moyenne du cosinus est nulle. On choisit alors
ω
1=
ω
2=
ω et donc k1=k2=k.
9
Chapitre 2 – Interférences à deux ondes
Condition sur la structure de l’interféromètre
Rappel : Emission spontanée de lumière par un atome à 2niveaux d’énergie
Retour à l’équilibre + émission
d’un train d’onde lumineux
Energie
Système
au repos
Etat excité
Etat
fondamental
Pulsation associée au train d’onde :
: constante de PLANCK réduite
Excitation
10