1°) Bac 97.4 PARTIE A. Un moteur série, utilisé pour la traction

Chapitres B.2.2 et B.3.2
1°) Bac 97.4
PARTIE A.
Un moteur série, utilisé pour la traction ferroviaire, a les caractéristiques nominales
suivantes :
tension d'alimentation : 1070 V ;
intensité : 530 A ;
puissance utile : 528 kW ;
vitesse de rotation : 2820 tr.min-1.
Les valeurs des résistances à chaud de l'inducteur et de l'induit sont respectivement 0,013 Ω et
0,027 Ω.
1. Pourquoi utiliser un moteur à excitation série, plutôt qu'à excitation indépendante, dans le
domaine de la traction ferroviaire ?
2. Dans le cas où l'on souhaiterait démarrer le moteur à l'aide d'un rhéostat, en utilisant pour
cela la tension nominale, calculer la valeur de la résistance de ce rhéostat sachant que le
courant de démarrage doit être limité à 1000 A. Quelle serait la puissance dissipée dans le
rhéostat lors du passage du courant maximal ?
3. Le moteur fonctionne en régime nominal. Calculer dans ce cas :
a) la puissance absorbée ;
b) le rendement ;
c) les pertes par effet Joule ;
d) l'ensemble des autres pertes en précisant leur origine ;
e) les moments du couple utile, du couple de pertes et du couple électromagnétique ;
f) la force électromotrice.
4.
a) De quel paramètre dépend la vitesse de ce moteur lorsqu'il fonctionne à courant constant ?
b) On souhaite faire varier la vitesse de rotation de ce moteur.
Quel dispositif électronique peut-on utiliser si la source d'alimentation est :
- de type continu fixe ;
- de type alternatif sinusoïdal ?
5. La valeur de la tension d'alimentation est fixée à 1100 V. Lors de ce fonctionnement le
moteur absorbe un courant d'intensité 513 A. En supposant que le flux sous un pôle est
proportionnel à l'intensité du courant traversant l'inducteur, calculer la vitesse de rotation
correspondant à cet essai.
6. En réalité, le moteur est alimenté par l'intermédiaire d'un pont mixte. Le courant absorbé
par le moteur, d'intensité instantanée i, n'est pas parfaitement lissé et peut être considéré
comme la superposition d'un courant continu d'intensité I (correspondant à la valeur moyenne
de i) et d'un courant purement sinusoïdal j de fréquence 100 Hz et de valeur efficace J = 0,28 I
(ondulation de i).
L'ondulation importante du courant i, donne naissance à un flux qui lui aussi varie de façon
importante. Pour atténuer ce phénomène, on choisit alors de "shunter" l'inducteur :
Bernaud J
1/8
Chapitres B.2.2 et B.3.2
ie
inducteur
i = I+j
i
is
shunt
Le shunt est un dipôle purement résistif dont la résistance notée s vaut 70 mΩ. L'inducteur a
une résistance notée r de 13 mΩ et une inductance notée λ de 0,7 mH.
a) On ne s'intéresse qu'à la composante continue I de i :
Ie
r, λ
I
Is
s
- Expliquer pourquoi l'inductance n'a pas d'influence en continu.
- Exprimer puis calculer Ie en fonction de I.
b) On ne s'intéresse qu'à l'ondulation j de i :
je
r, λ
j
js
s
Soit J, Je et Js les intensités complexes correspondant à j, je, et js.
Ecrire l'égalité des tensions aux bornes de l'inducteur et du shunt.
En déduire l'expression de Js en fonction de Je.
Exprimer ensuite J en fonction de Je.
s
En déduire la relation entre valeurs efficaces : J e =
J.
2
(s + r ) + ( λϖ ) 2
J
c) On peut mesurer le taux d'ondulation du flux par le rapport O1 =
en l'absence de
I
O
Je
en présence de shunt. Le rapport e = 1 mesure
shunt et par le rapport O2 =
O2
Ie
l'efficacité du shunt.
Calculer e avec les valeurs numériques précédentes.
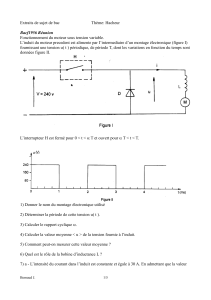
Partie B : Etude du hacheur
On dispose d'une source de tension continue de 1500 V. On alimente le moteur à l'aide du
dispositif suivant :
Bernaud J
2/8
Chapitres B.2.2 et B.3.2
iH
Ug
H
L
D
i
Rt
v
u
E
iD
Tous les composants sont supposés parfaits.
Le moteur a été remplacé par son modèle électrique équivalent. Rt tient compte des
résistances d'induit et d'inducteur. L tient compte de l'inductance de la bobine de lissage et de
celle de l'induit du moteur.
H est un interrupteur électronique unidirectionnel commandé périodiquement. La période sera
notée T et la fréquence correspondante f.
1. Citer deux composants électroniques permettant de réaliser H.
2. On a relevé l'intensité i du courant dans le moteur en fonction du temps (voir document
réponse). Dessiner sur le document réponse et en concordance des temps v(t), iD(t) et iH(t).
3.
a) En déduire la fréquence de fonctionnement de l'interrupteur H, le rapport cyclique α
de la tension v ainsi que sa valeur moyenne notée V (avant l'application numérique on
donnera la relation liant V , α et Ug).
b) Calculer les valeurs moyennes des intensités des courants i, iD, iH. Comment les
mesurer ?
c) Calculer la valeur efficace de la tension v. Quel type de voltmètre doit-on employer
pour mesurer une telle tension ?
4. Que vaut la tension moyenne aux bornes de la bobine, supposée parfaite, L ?
5. Donner alors la relation entre la valeur moyenne V de la tension v et la valeur moyenne de
la tension u notée U . En déduire la relation liant U , α et Ug.
6. On souhaite que la tension moyenne aux bornes du moteur ne dépasse pas 1100 V. Quelle
doit être alors la valeur maximale du rapport cyclique ? Sachant que l'intensité du courant au
démarrage doit être limitée (sans rhéostat) à 1000 A, calculer la valeur minimale du rapport
cyclique pour que le moteur démarre.
2°) Bac 98.4
Étude d'un moteur à courant continu alimenté par un hacheur
Les parties A et B sont indépendantes
Partie A : Étude du moteur
La plaque signalétique d'une machine à courant continu à excitation indépendante indique les
valeurs
nominales suivantes :
Bernaud J
3/8
Chapitres B.2.2 et B.3.2
Tension d'induit : UN=90 V
Intensité du courant d'induit :
IN=10 A
Puissance utile :
PuN=750 W
Fréquence de rotation:
nN=1500 tr.min-1
Le moteur est parfaitement compensé (son flux par pôle ne dépend que du courant
d'excitation).
Le courant d'excitation reste constant dans tout le problème.
La valeur de la résistance de l'induit est R = 0,40 Ω
.
I - On considère le fonctionnement nominal ; calculer:
1) La force électromotrice EN.
2) Le moment du couple électromagnétique TEN
3) Le moment du couple utile TuN
4) Le "rendement de l'induit".
Il - La vitesse angulaire de rotation Ω du moteur est exprimée en rad.s-1.
1) Montrer que E = aΩ ; calculer la valeur numérique de a.
2) En déduire que TE = 0,547 I ; I est le courant de l'induit.
III - A partir du fonctionnement nominal, on supprime la charge du moteur, qui désormais,
fonctionne à vide.
Dans cette opération, la fréquence de rotation varie. On la ramène alors à sa valeur
nominale nN.
1) Sur quelle grandeur faut-il agir et dans quel sens ? Justifier le sens croissant ou
décroissant.
2) Donner la valeur de la f.é.m à vide E0 ; en déduire la tension aux bornes de l'induit U,,
si l'intensité du courant d'induit à vide est I0 = 1,28 A.
3) Calculer la somme des pertes dans le fer et des pertes mécaniques du moteur notée pc.
4) Vérifier que le moment du couple de pertes noté Tp est égal à 0,70 N.m ; on admet
qu'il reste constant dans le problème.
IV- Le moteur est alimenté sous une tension d'induit U réglable de O à 2OV; la charge exerce
un couple résistant constant dont le moment est TR = 4,77 N.m.
1) Montrer que dans ces conditions le couple électromagnétique TR et le courant
d'induit I restent constants et donner leurs valeurs.
2) Démontrer que l'on peut écrire Ω = 1,83U - 7,3 ; en déduire que n = 17,5U - 70 (n
étant la fréquence de rotation du moteur exprimée en tr.min-1).
3) Donner le mode opératoire pour le démarrage du moteur et déterminer sa tension de
démarrage.
Étude du hacheur
L'alimentation de l'induit du moteur précédent est réalisée avec un hacheur série de période T fixe
et de rapport cyclique α réglable (0≤ α ≤ 1).
Ua est une tension continue positive fixe.
Bernaud J
4/8
Chapitres B.2.2 et B.3.2
Le hacheur est représenté sur le schéma suivant:
iH
H
L
uL
iD
uH
u
D
i
M
uM
.
L'interrupteur commandé H et la diode D sont supposés parfaits.
L est une inductance de lissage de résistance négligeable assurant une conduction ininterrompue.
H est fermé de 0 à αT.
H est ouvert de αT à T.
I- Étude expérimentale du hacheur
1) On dispose d'une résistance de visualisation rv et d'un oscilloscope bicourbe dont la
voie Y2 peut être inversée.
La masse de l'oscilloscope est obligatoirement reliée au point M (voir document réponse
n° 1). On veut visualiser simultanément les grandeurs suivantes (avec éventuellement, de
petites approximations que l'on explicitera : u est la tension aux bornes de l'ensemble
moteur et inductance de lissage)
a) u(t) et i(t).
b) u(t) et iD(t).
c) u(t) et iH(t).
Compléter les schémas a, b, c correspondants du document réponse n°1, et indiquer le
branchement des voies Y1 et Y2 ainsi que l'emplacement de la résistance rv dans
chaque cas.
2) Préciser sur le document réponse n° 1, pour chaque cas (a, b, c), la position du zéro
pour avoir le maximum de sensibilité verticale ainsi que la position des commutateurs
d'entrée AC ou DC.
3) Expliquer le rôle de la diode D.
II Étude du fonctionnement pour une valeur constante du rapport cyclique α
1) La forme de la tension rvi aux bornes de la résistance rv est donnée sur le document
réponse n° 2:
a) En déduire la fréquence f de fonctionnement et le rapport cyclique α .
b) Sachant que rv = 0,10Ω, calculer la valeur maximale imax ,la valeur minimale imin et
la valeur moyenne < i > de l'intensité du courant i(t).
2) Représenter les formes de iH t), de iD (t) et de u(t) sur le document réponse n° 2.
3) Donner en la justifiant l'expression de la valeur moyenne < u > de u(t) en fonction de α et
de Ua.
4) On donne < u > = 90 V: en déduire la valeur de Ua
Bernaud J
5/8
Chapitres B.2.2 et B.3.2
Document réponse (à rendre avec la copie)
i (A)
570
490
t (ms)
0 0,167
v (V)
1500
1000
500
t (ms)
0 0,167
i D (A)
570
490
t (ms)
i H (A)
0 0,167
570
490
t (ms)
0 0,167
Bernaud J
6/8
Chapitres B.2.2 et B.3.2
Problème 2-Partie B : Document réponse n°1 à rendre avec la copie
a
iH
H
Position du zéro ?
AC ou DC ?
L
i
iD
u
M
D
M
b
iH
H
Position du zéro ?
AC ou DC ?
L
i
iD
u
M
D
M
c
iH
H
Position du zéro ?
AC ou DC ?
L
i
iD
u
M
D
M
Bernaud J
7/8
Chapitres B.2.2 et B.3.2
Problème 2-Partie B : Document réponse n°2 à rendre avec la copie
rv.i(V)
1
0,2
t(ms)
0
0,1
iH(A)
10
2
t(ms)
0
0,1
iD(A)
10
2
t(ms)
0
0,1
u(V)
Ua
0
Bernaud J
t(ms)
0,1
8/8