Chap 18 droites remarquables triangle

DROITES REMARQUABLES DU TRIANGLE ET CERCLES
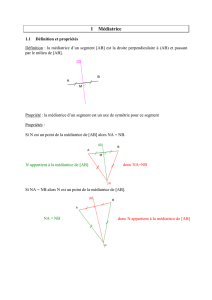
I Droites remarquables :
Précise la nature des droites dans chacun des triangles précédents.
(a) est la hauteur issue de B. H est le pied de la hauteur.
(b) est la médiatrice de [AS].
(c) Est la médiane issue de T.
(d) Est la bissectrice de l’angle IPD
II Bissectrices
1) Définition 1:
La bissectrice d’un angle est l’axe de symétrie de cet angle.
2) Définition 2 :
La bissectrice d’un angle est une demi-droite partageant un angle en deux angles adjacents de même mesure.
3) Construction de la bissectrice d’un angle :
On a OA =OB et AM=MB. donc (OM) est la médiatrice de [AB]. Donc B est l’image de A par la symétrie
d’axe (OM). Par conséquent la bissectrice est l’axe de symétrie de cet angle.
4) Equidistance :
Sur le dessin précédent compare les longueurs de M à (OA) et de M à (OB)
Que constates-tu ? Les deux distances sont égales.
Propriétés :
Si un point est sur la bissectrice d’un angle alors il est à égale distance (ou équidistant) des deux côtés de cet
angle.
Réciproquement, si un point est à égale distance de deux côtés d’un angle alors il est sur la bissectrice de cet
angle.
B
U
T
(a)
H
A
M
S
I
(b)
U
B
T
R
(c)
I
D
P
(d)
E
M
A
B
O

III Cercles
1) Tangente :
Construis un cercle de centre O. Place un point A sur ce cercle.
Construis la droite (d) perpendiculaire en A au rayon [OA].
Place un point M distincts de A sur la droite (d).
1) Explique pourquoi OM>OA.
2) En déduire que la droite (d) ne coupe le cercle qu’au seul point A.
1) OA est la distance de O à (d) donc OM>OA.
2) Quel que soit un point M de (d) distincts de A, on a OM>OA or OA
est le rayon du cercle donc M n’appartient pas au cercle.
Par conséquent A est le seul point appartenant au cercle et à la droite (d).
2) Définition :
La tangente d’un cercle en un point est la droite perpendiculaire au rayon en ce point
3) Cercle inscrit :
a) Construis un triangle ABC tel que BAC = 80°, ABC = 40° et AB = 10 cm.
b) A la règle et au compas, construis les bissectrices des angles BAC et ABC .
1) Démontre IK=IL
On sait que [AI) est la bissectrice de BAC .
Or, si un point est sur la bissectrice d’un angle alors il est à égale distance (ou équidistant) des deux côtés de cet
angle.
Donc IJ = IL De même IJ = IK Par suite IL=IK.
2) Démontre que I appartient à la bissectrice de ACB .
On sait que IL = IK
Or, si un point est à égale distance de deux côtés d’un angle alors il est sur la bissectrice de cet angle.
Donc I appartient à la bissectrice de l’angle ACB .
Propriété (admise) :
Les bissectrices des angles d'un triangle sont concourantes. Le point de concours est à égale distance des
trois côtés du triangle : c’est le centre du cercle tangent aux trois côtés du triangle.
Trace le cercle de centre I et de rayon IL. Que constates-tu ?
On constate que le cercle est tangent aux trois côtés du triangle.
Propriété : ( admise)
Le point de concours est à égale distance des trois côtés du triangle : c’est le centre du cercle tangent aux
trois côtés du triangle.
Définition :
Le cercle tangent aux trois côtés d’un triangle s’appelle le cercle inscrit dans ce triangle.
O
A
(d)
Appelle I le point d’intersection des deux bissectrices.
Appelle IJ la longueur de I à (AB)
Appelle IK la longueur de I à (BC)
Appelle IL la longueur de I à (AC)

IV 1er rappel : les Médiatrices
1) Définition de la médiatrice d’un segment :
La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
2) Propriété des médiatrices d’un triangle :
a) Construis un triangle ABC tel que AB = 8 cm, AC = 7 cm et BAC = 100°.
b) A la règle et au compas, construis le cercle circonscrit au triangle ABC.
Propriété : Les médiatrices d’un triangle sont concourantes.
Leur point d’intersection est à égale distance des 3 sommets du triangle ; il est donc le centre du cercle
circonscrit au triangle.
V 2ème rappel : les Hauteurs
1) Définition :
Une hauteur d’un triangle est une droite passant par un sommet et perpendiculaire au support du côté opposé à
ce sommet.
2) Propriété des hauteurs d’un triangle :
a) Construis un triangle ABC tel que ABC = 105°, AB = 5 cm et AC = 10 cm.
b) Construis l’orthocentre du triangle ABC.
Propriété (admise) :
Dans un triangle, les hauteurs sont concourantes en un point appelé orthocentre
IV 3ème rappel : les Médianes
1) définition :
Une médiane d'un triangle est une droite passant par un sommet et par le milieu du côté opposé à ce sommet.
On peut faire la démonstration concernant l’intersection des médianes.
c) Démontrer que si O est le point d'intersection de deux
médiatrices, alors il est aussi sur la troisième et en déduire que le
cercle de centre O et de rayon [OA] passe par les points B et C
Soit O le point d'intersection des médiatrices de [AB] et de [AC]
alors, OA = OB et OA = OC donc on a OB = OC.
Le point O est donc sur la troisième médiatrice et OA = OB = OC

2) Propriété des médianes d’un triangle :
a) Construis un triangle ABC tel que AC = 8 cm, BC = 7 cm et AB = 10 cm.
b) Construis le centre de gravité.
Propriété 1 : les médianes d'un triangle sont concourantes en un point appelé centre de gravité.
Propriété 2 : le centre de gravité d'un triangle est situé au 2
3 de chaque médiane à partir du sommet.
Ainsi dans le triangle ABC : AG = 2
3 AI, BG = 2 3 BJ, CG = 2 3 CK.
VII Triangles particuliers
1) triangle isocèle
Construis un triangle TIC isocèle en I. Construis la médiatrice du segment [TC].Que constates-tu ?
On constate que la médiatrice est la hauteur issue de I, la médiane issue de I et la bissectrice de l’angle TIC .
Propriété :(admise)
Si un triangle est isocèle alors la hauteur issue du sommet principal est aussi une médiane, une médiatrice et
une bissectrice.
2) triangle équilatéral
Construis un triangle BUT équilatéral. Construis les trois bissectrices du triangle. Que constates-tu ?
On constate que les bissectrices sont aussi les hauteurs, les médianes et les bissectrices.
Propriété :(admise)
Si un triangle est équilatéral alors les médianes sont aussi des médiatrices, des hauteurs et des bissectrices.
T C
I
B U
T