Évaluer la précision d`une carte avec le nombre de bits

63
S olutions
MESURES 766 - JUIN 2004
D
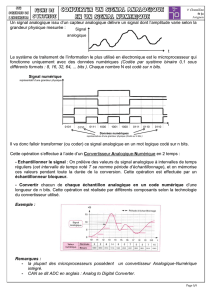
e nos jours, il ne suffit plus
d’évaluer la précision d’une
carte d’acquisition de données
en vérifiant uniquement la
conversion analogique-numérique ou les
spécifications du domaine temporel (la linéa-
rité, la précision relative, etc.). Des critères
comme le temps de conversion, les perfor-
mances de l’étage analogique ou la réponse
en fréquence jouent un rôle croissant pour
déterminer la performance globale d’une
carte de conversion analogique-numérique.
Si l’on évalue une carte seulement à partir
des spécifications de précision, on ne se rend
compte que d’une partie de ses perfor-
mances. La précision relative est définie
comme la plus grande différence entre la
valeur analogique du signal et la valeur
retournée par la carte après numérisation.
Pour déterminer ce paramètre, on injecte sur
la carte une tension d’entrée connue que l’on
fait varier entre 0 et 10V par exemple (pour
un convertisseur dont la gamme d’entrée est
de 10V). Puis on relève pour chaque valeur
injectée, la valeur binaire retournée par le
convertisseur que l’on compare à la tension
d’entrée de référence. La plus grande diffé-
rence entre cette valeur binaire convertie en
tension et la tension d’entrée détermine la
précision relative de la carte. Ce paramètre
est considéré comme une spécification tem-
porelle parce que la mesure est toujours fai-
te à faible vitesse d’échantillonnage en utili-
sant une seule entrée analogique.
Bien que cette manipulation puisse refléter
certaines utilisations de la carte, la plupart
des applications utilisent un grand nombre
d’entrées analogiques à des périodes
d’échantillonnage de 1 échantillon par secon-
de à plus de 1 million d’échantillons par
seconde. A des vitesses plus élevées et avec
des acquisitions multivoies, la précision rela-
tive n’est plus un bon indicateur de l’inté-
grité d’une carte. Pour être certain que les
données acquises soient fiables, seuls les para-
mètres fréquentiels
permettent de
mettre en éviden-
ce les perfor-
mances d’une car-
te. Le nombre de
bits effectifs (en
anglais ENOB,
pour Effective
Number Of Bits)
facilite l’apprécia-
tion de la précision
d’une carte d’ac-
quisition.
Obtenu à partir du
rapport signal sur
bruit (en anglais
SNR, pour Signal
to Noise Ratio)
▼
Pour une application donnée, comment choisir une carte d’acquisition de signaux, tout en étant certain d’obtenir la préci-
sion souhaitée? Une spécification appelée “nombre de bits effectifs” (ENOB, pour Effective Number of Bit en anglais) facili-
te l’évaluation des performances d’une carte.
En bref
Tout système d’acquisition
comporte des limitations
intrinsèques qui sont sour-
ce de bruit, de non linéarité
et de distorsion des harmo-
niques du signal
Les spécifications clas-
siques d’une carte d’acqui-
sition comme la résolution
du convertisseur ou la pré-
cision relative ne rendent
pas compte de ces limita-
tions
Un critère appelé nombre
de bits effectifs permet de
se faire une bonne idée de
la précision globale de la
carte
ACQUISITION SUR CARTE
Évaluer la précision
d’une carte avec le nombre
de bits effectifs
Toute carte d’acquisition comporte des imperfections qui sont source de bruit, de non linéarité et de distorsion du signal.

64
S olutions
MESURES 766 - JUIN 2004
d’une carte, le nombre de bits effectifs per-
met d’évaluer la performance globale d’un
système de conversion analogique-numé-
rique en prenant en compte le bruit introduit
par le système ainsi que ses nombreuses
imperfections.
L’insuffisance des spécifications
temporelles
L’étage d’entrée analogique d’une carte d’ac-
quisition de données multivoies possède un
multiplexeur, un amplificateur de gain pro-
grammable et un échantillonneur-bloqueur
qui précède le convertisseur analogique/numé-
rique. La fonction de transfert de l’étage d’en-
trée (c’est-à-dire le rapport de l’entrée sur la
sortie) impacte fortement le signal qui sera à
l’entrée du convertisseur analogique/numé-
rique et par conséquent le résultat numérisé.
Toute déformation de spectre apparaissant à
travers l’étage d’entrée est également convertie
avec le signal d’origine, entraînant une sortie
imprécise. Les non linéarités dynamiques intro-
duites au niveau de cet étage d’entrée peuvent
devenir une source d’imprécision importante.
Par ailleurs, tout convertisseur a ses propres
limitations : les non linéarités différentielles,
les fluctuations d’ouverture, les fluctuations
d’horloges, le temps de conversion, les
conversions erronées, le bruit et les distor-
sions… Bref, négliger la conception de l’éta-
ge d’entrée analogique comme celle du
convertisseur engendre la dégradation de la
précision du système d’acquisition de don-
nées considéré.
A titre d’exemple, les systèmes multivoies
utilisent souvent un multiplexeur pour com-
muter de voie à voie. Une erreur fréquente
dans le calcul de la précision d’un tel systè-
me consiste à évaluer la précision relative en
faisant des mesures sur une seule voie. Ceci
est dû au fait que l’on ne prend pas en comp-
te les erreurs dues au temps de réponse de la
voie d’entrée. Le temps de réponse donne
une meilleure estimation des performances
d’acquisition d’un sous-système d’entrées
analogiques que les caractéristiques de pré-
cision. Ce temps de réponse correspond au
temps nécessaire au multiplexeur pour sta-
biliser sa sortie. Celui-ci est le fruit d’un
ensemble de paramètres : l’impédance de la
source, les parasites à l’entrée du multiplexeur
et l’effet capacitif en sortie. De plus, l’ampli-
ficateur ajoute son propre temps de répon-
se. Si les voies sont commutées avant que
l’entrée de la voie précédente soit remise à
zéro, une valeur résiduelle est ajoutée à la
valeur de la voie suivante. Il faut typique-
ment environ neuf constantes de temps RC
(résistance-capacité) à un signal pour arri-
ver à 0,01 % de sa valeur initiale. Par consé-
quent, avec 1 kΩd’impédance à la source et
100 pF de capacité en sortie, la constante de
temps est de 100 ns. Multiplié par neuf, cela
représente presque 1 µs. Si la première voie
était à une valeur de 10V et que vous ne lais-
sez pas assez de temps pour l’établissement,
une partie de ces 10V sera ajoutée à la valeur
de la voie suivante. Ce serait le cas avec un
échantillonnage de voie à 250 Kéch./s qui lit
une nouvelle voie toutes les 4 µs. A l’heure
actuelle, aucune spécification de conversion
sur une seule voie ne peut mettre en évi-
dence cette source d’erreur.
Même les tests de conversion de données qui
sont valables sur une voie perdent leur inté-
rêt avec les nouvelles techniques de conver-
sion de données. Par exemple, un test fré-
quent consiste à calibrer une carte
d’acquisition de données avec un signal plei-
ne échelle bipolaire et à vérifier la valeur du
niveau zéro. Pour des méthodes de conver-
sion par approximations successives ou
d’autres méthodes de conversion, vérifier le
niveau zéro ou le point à mi-échelle repré-
sente le pire des tests. Cela revient à compa-
rer le bit de poids fort (Most Significant Bit
MSB en anglais qui vaut la moitié de la valeur
pleine échelle) à la somme des bits restants
qui vaut 1 LSB (Least Significant Bit, bit de
poids le plus faible) de moins que le MSB.
Bien que ce test ait été accepté pendant des
années, ses résultats ne sont pas assez signi-
ficatifs pour les nouvelles architectures de
convertisseurs à approximations successives
ou à conversion sigma-delta. Même si le
convertisseur a un temps de réponse rapide
et de bonnes caractéristiques de conversion,
il peut introduire des erreurs en raison de
l’instabilité de la distorsion des harmoniques
qu’engendre l’échauffement du composant
à vitesse d’échantillonnage élevée.
Enfin, un système d’acquisition de données
ayant un étage d’entrée mal conçu engendre
souvent de la distorsion d’harmonique (une
conséquence de la non-linéarité de l’étage).
Le taux de distorsion harmonique (THD
pour Total Harmonic Distorsion en anglais,
appelé aussi distorsion harmonique totale)
est le rapport entre la somme des moyennes
quadratiques (ou valeurs efficaces) des har-
moniques du signal sur la moyenne qua-
dratique de sa fréquence fondamentale. Le
taux de distorsion harmonique est devenu
très important pour l’évaluation de la préci-
sion d’une carte d’acquisition de données.
Les erreurs dues à la distorsion de l’étage
d’entrée se retrouvent à l’entrée du conver-
tisseur analogique/numérique et ne peuvent
être supprimées à sa sortie. La distorsion des
harmoniques et d’autres sources d’erreurs
non-linéaires diminue le rapport signal sur
bruit d’une carte.
Appréhender le nombre
de bits effectifs
Le nombre de bits effectifs, lui, donne une
mesure simple du rapport signal sur bruit
d’une carte permettant d’appréhender sa pré-
cision dynamique. Le nombre de bits effec-
tifs peut être obtenu à partir de la définition
théorique du rapport signal sur bruit. Pour
un signal d’entrée sinusoïdal, le rapport signal
sur bruit théorique d’un signal échantillon-
né avec un convertisseur idéal est donné par :
SNR = (6,02N+1,76) dB où N
est la résolution du convertisseur
Le bruit n’est ici que du bruit de quantifica-
tion. Dans le cas idéal, un convertisseur de
12 bits de résolution a un rapport signal sur
bruit théorique de 74 dB ; un convertisseur
de 16 bits a un rapport signal sur bruit théo-
rique de 98 dB.
La résolution Ns’exprime donc en fonction
du rapport signal sur bruit sous la forme :
N = (SNR-1,76)/6,02
Pour une entrée sinusoïdale d’une certaine
fréquence, le nombre de bits effectifs calcu-
lé à partir du SNR mesuré est :
ENOB = (SNR mesuré – 1,76)/6,02
En mesurant le rapport signal sur bruit, on
peut en déduire le nombre de bits effectifs
d’un sous-système analogique. Pour le rap-
port signal sur bruit théorique SNR, on a :
ENOB = (SNR-1,76)/6,02=N
La résolution du convertisseur représente le
nombre de bits effectifs théorique que le sys-
tème peut atteindre. Dans la réalité, le
nombre de bits effectifs n’atteint jamais la
résolution réelle du convertisseur analo-
Le nombre de bits effectifs permet de se faire une bonne idée de la précision globale d’un sys-
tème d’acquisition.

65
S olutions
MESURES 766 - JUIN 2004
gique/numérique. Cependant, plus le
nombre de bits effectifs est proche de la réso-
lution de la carte, meilleures sont les perfor-
mances de celle-ci.
Ainsi, le nombre de bits effectifs donne une
mesure représentative de la précision dyna-
mique basée sur un seul paramètre. Il s’agit
d’un excellent critère pour connaître la capa-
cité d’un sous-système à acquérir et numé-
riser correctement des signaux dynamiques
dans une plage de fréquence donnée.
Comment mesurer le nombre
de bits effectifs?
Le point clé pour calculer le nombre de bits
effectifs d’une entrée analogique d’un sous-
système est de mesurer son rapport signal
sur bruit. Le moyen le plus simple de le fai-
re est de faire l’acquisition d’une série
d’échantillons en numérisant un signal d’en-
trée sinusoïdal à la pleine échelle. Puis il faut
tronquer la séquence d’échantillons en uti-
lisant l’une des nombreuses fenêtres de pon-
dération. Ensuite, la transformée de Fourier
est réalisée sur chaque fenêtre de pondéra-
tion. On regarde enfin chaque résultat; la
fenêtre dont l’amplitude est la plus grande
permet de déterminer la fréquence fonda-
mentale. Le rapport signal sur bruit est une
mesure de la largeur de bande du bruit intro-
duit dans le signal. Il est le rapport entre la
moyenne quadratique de la somme de la fré-
quence fondamentale et de la moyenne qua-
dratique de la somme de tous les autres har-
moniques inférieurs à la fréquence de
Nyquist (à l’exclusion de la composante
continue). Pour être tout à fait juste, ce résul-
tat est le rapport du signal sur le bruit et la
distorsion (S/(N+D)) qui est une définition
généralement acceptée du rapport signal sur
bruit. Le rapport signal sur bruit mesuré est
alors utilisé pour calculer le nombre de bits
effectifs de la carte.
Que se passe-t-il si l’on n’utilise pas une car-
te d’acquisition de données avec un nombre
de bit effectif élevé? Le suréchantillonnage
ou le moyennage des résultats peuvent-ils
rehausser leur précision? Certes, les calculs
peuvent aider mais ne peuvent pas corriger
toutes les erreurs introduites par un design de
mauvaise qualité.
Si par exemple, vous surveillez des thermo-
couples avec un bruit significatif, un moyen-
nage pourra améliorer la précision générale
des résultats. La plupart des thermocouples ne
sont pas très précis (un thermocouple de
Type J a une précision de l’ordre de 0,75 %
soit environ 2,2 °C). Si l’on envisage d’ac-
quérir 100 échantillons et ensuite de faire
une moyenne des résultats, on éliminera
beaucoup de bruit et d’incertitude prove-
nant du thermocouple. Cependant, si vous
surveillez des signaux plus rapides sur une
gamme de tension plus large, faire la moyen-
ne ne devrait pas être d’une grande aide. Et
si l’étage d’entrée de la carte d’acquisition
de données a une faible linéarité et qu’il pro-
duit de la distorsion, faire la moyenne ne
pourra pas compenser les erreurs.
Diminuer la fréquence d’échantillonnage
peut améliorer les performances de la carte
si elle souffre d’un mauvais temps de répon-
se mais cette technique réduit fortement sa
bande passante et sa capacité à numériser
avec précision des signaux rapides.
Kevin Sullivan,
Data Translation Engineering
Texte proposé par Atemation