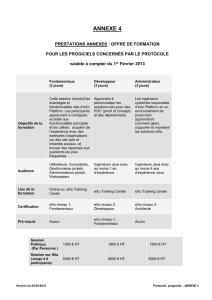
TD1LMD14_15

TD 01 de physique 1ère année SNV/LMD 2014/2015
Exo. 1 :
Donnez l’unité et la dimension convenables pour la mesure de:
 Surface d’un habitat, surface agricole, surface d’un pays, surface d’une puce (électronique).
 Puissance d’une lampe électrique, puissance d’un véhicule, puissance d’un four électrique.
 Masse des bijoux, qualité de l’or, qualité du papier.
 Vitesse d’une voiture, vitesse du vent, vitesse d’horloge d’un micro-ordinateur.
 Pression atmosphérique, pression des roues d’automobiles, tension artérielle.
 Capacité d’une mémoire électronique.
 Taille d’écran d’un micro-ordinateur
Exo. 2 :
a) Trouvez la dimension de X et Y dans chaque cas:
Avec F: force, p: puissance, P: pression, i: courant électrique, t: temps, g: accélération, V: volume,
v: vitesse, h: hauteur, R: résistance électrique, C: capacité électrique, Lo: inductance électrique,
m: masse, S: surface, ωo: pulsation, f : fréquence.
Exo. 3 :
Trouvez l’expression de la vitesse en fonction de la puissance, la masse et le temps.
Exo. 4 :
A partir d’un calcul dimensionnel, trouvez l’expression de la période To d’un pendule simple, en fonction
de sa longueur l et l’accélération de pesanteur g.
Exo. 5 :
En utilisant une analyse dimensionnelle, trouvez l’expression de δ (mesurée en m), en fonction de
(mesurée en m3kg/A2s3) et μ (mesurée en m.kg/A2s2) et f (mesurée en Hz).
Exo. 6 :
a)- Dans un repère cartésien OXY on donne   et   .
Calculez et représentez :  ,  , V1 , V2 ,  ,   ,  , 
 , 
, 
b)- Refaire le même exercice pour:
 et  .   et  .
 et   .   et  .
Exo. 7 :
a)- Dans un repère cartésien OXYZ on donne  et  .
Calculez et représentez :  ,  , V1 , V2 ,  ,   ,  , 
 , 
,  ,
,  ,   et   .
En utilisant le produit scalaire trouvez l’angle  entre  et .
b)- Refaire le même exercice pour :
et  et 
et  et 
Exo. 8 :
On donne  ,  et  .
Calculez le produit mixte : 
 et 
Calculez le double produit vectoriel : 
 et 