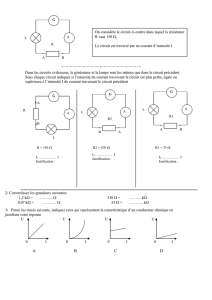
2. Signal bidirectionnel 3. Signal périodique 4. Signal alternatif 5

2. Signal bidirectionnel
Correspond à un courant circulant dans les deux sens, donc dont l'intensité est tantôt positive et tantôt négative.
3. Signal périodique
C'est un signal qui se répète régulièrement égal à lui-même.
4. Signal alternatif
Un signal alternatif est à la fois périodique et bidirectionnel. De plus on considère généralement que cette
appellation implique une symétrie entre l'évolution positive et l'évolution négative.
5. Notion de période et de fréquence
La période T est la durée minimale au bout de laquelle le signal se répète égal à lui-même, elle s'exprime donc en
seconde (de symbole s) dans le Système International (S.I.).
La fréquence est le nombre de période par seconde : f =
1
T
(avec T en s, f en Hz)
6. Valeur maximale et valeur instantanée
La valeur instantanée est la valeur prise par l'intensité i (ou par la tension u) à l'instant t considéré. Elle est donc
comprise entre la valeur maximale Im (ou Um) et la valeur minimale.
7. Valeur moyenne et valeur efficace
a. Valeur moyenne
C'est la moyenne des valeurs instantanées prises sur une période. Elle est égale à la « surface » comprise entre la
courbe (représentative des variations de i en fonction du temps durant une période) et l'axe des abscisses divisée par la
période.
En réalité S n'est pas une surface c'est une charge électrique puisque c'est le produit d'une intensité par un temps.
C'est en fait la charge électrique totale Qtotal qui passe à travers une section du circuit pendant une période :
i
=
Qtotal
T
b. Valeur efficace
α) Préambule Un conducteur ohmique est un dipôle qui obéit à la loi d'Ohm, c'est-à-dire que la tension à ses
bornes uR est, à chaque instant, proportionnelle à l'intensité i du courant électrique qui le
traverse :
uR = R ×i
La constante de proportionnalité R est une caractéristique du conducteur ohmique :
c'est sa résistance.
Un conducteur ohmique convertit intégralement l'énergie électrique qu'il absorbe
(Q = U·I·Δt = R·I²·Δt) en chaleur, c'est l'effet Joule.
β) Différents points de vue
- La valeur efficace d'une intensité variable correspond à la valeur d'une intensité continue qui provoquerait
le même effet Joule en traversant le même conducteur ohmique.
- La valeur efficace d'une intensité ou d'une tension est également la valeur donnée par un multimètre.
- Mathématiquement c'est la racine carrée de la moyenne du carré de i (ou de u) : I =
i2
-Pour un signal alternatif sinusoïdal : I =
Imax
2
7

III. Le régime sinusoïdal
1. Définition
Une grandeur variable est dite sinusoïdale si sa valeur instantanée s'exprime en fonction de t à l'aide de la fonction
sinus ou cosinus.
Exemples : u(t) = Um·sin(ω·t + φ) ; i(t) = Im·cos(ω·t + φ')
Les alternateurs des centrales électriques nous fournissent des tensions et des courants sinusoïdaux, d'où
l'importance de ce régime.
2. Phase, phase à l'origine
Considérons un vecteur
Um
de longueur Um, tournant à la vitesse angulaire ω et faisant, à t = 0, un angle φ avec un
axe de référence horizontal :
« tourner à la vitesse angulaire ω » signifie qu'à
l'instant t, le vecteur aura tourné d'un angle (ω·t), il fera donc,
à cet instant t, un angle (ω·t + φ) avec l'axe de référence :
Les angles (ω·t + φ) et φ
sont respectivement la phase à l'instant t
et la phase à l'origine du signal.
Cherchons l'expression de la projection du vecteur
Um
sur l'axe horizontal, qui est également l'axe de référence.
On voit sur la figure ci-dessous un triangle rectangle.
Or dans un tel triangle :
cos (ω·t + φ) =
côté adjacent
hypothénuse
⇒cos (ω·t + φ) =
x
Um
⇔x = Um·cos (ω·t + φ)
Or c'est justement l'expression d'une tension
dite « sinusoïdale » vue précédemment :
u(t) = Um·cos(ω·t + φ)
C'est-à-dire que l'on vient de démontrer que la projection de ce vecteur tournant
Um
(introduit artificiellement : il
ne correspond à aucune réalité physique) est la valeur instantanée d'une grandeur sinusoïdale : une tension ou une intensité
ou autres.
8
Axe de référence
φ
Sens positif de rotation
des vecteurs de
Fresnel
+
O
Um
à t = 0
Axe de référence
O
Um
à t quelconque
ω·t + φ
x
Projection
orthogonale sur l'axe horizontal
Axe de référence
+
O
à t quelconque
Um
ω·t + φ