Réseaux blazés binaires : définition

Réseaux blazés binaires : définition
La méthode établie de fabrication des optiques diffractives consiste à imposer à la surface des
composants des reliefs continus (échelette) séparés par des discontinuités, voir figure a).
Quelques PME américaines et quelques
Instituts de recherche commercialisent des
composants à la demande. Alternativement, on peut
imaginer des réseaux blazés en indice (voir Fig. b)
qui, aux pertes par réflexion de Fresnel près et pour
de grandes périodes, sont strictement équivalents
aux réseaux échelettes si n(x)h = nh(x), expression
traduisant simplement l’égalité des chemins optiques
à la côte x entre un réseau (blazé en indice) de
hauteur h constante présentant un profil d’indice
n(x) et un réseau (échelette) gravé dans un matériau
homogène d’indice n et de hauteur variable h(x). Il
est très difficile de fabriquer des réseaux blazés en
indice, mais on peut s’en approcher en considérant
des composants structurés à une échelle plus fine
que la longueur d’onde. Sur la Fig. c), le motif
comporte plusieurs traits par période. La largeur de
ces traits augmente progressivement de la gauche
vers la droite sur une période ; la lumière incidente
dans la partie gauche « ressent » plutôt un matériau
de faible indice, celle incidente dans la partie droite
plutôt un matériau de fort indice. L’augmentation
progressive de la largeur des traits mime ainsi un
gradient d’indice parallèle au substrat. Le composant
est blazé et son profil est binaire.
Sur cette idée, grâce aux progrès récents en
modélisation électromagnétique des réseaux, notre
équipe, en collaboration avec le LMM à Bagneux, a
obtenu en 1998-2000 des composants diffractifs qui
opèrent en régime d’indice effectif. La photographie
ci-contre obtenue au microscope électronique à
balayage montre un exemple de réalisation*. Il
s’agit d’un réseau de période 3λ constitué de cinq
piliers par période qui est conçu pour être blazé à
633 nm. Son efficacité de diffraction en incidence
normale est de 82% en lumière non polarisée.
* S. Astilean, Ph. Lalanne, P. Chavel, E. Cambril and H. Launois, Opt. Lett. 23, 552-554 (1998). Ph. Lalanne, S.
Astilean, P. Chavel, E. Cambril and H. Launois, Opt. Lett. 23, 1081-1083 (1998). Ph. Lalanne, S. Astilean , P.
Chavel, E. Cambril and H. Launois, Optics & Photonics News 9, 21-22 (Déc. 1998). Ph. Lalanne, S. Astilean , P.
Chavel, E. Cambril and H. Launois, J. Opt. Soc. Am. A 16, 1143-1156 (1999). L. Lee, Ph. Lalanne, J.C. Rodier
and E. cambril, Opt. Lett. 25, 1690-1692 (2000).
a)
b)
c)
a) profil continu type réseau à échelette classique
(période Λ). Aux pertes de Fresnel près, ce réseau est
100% efficace aux grandes périodes : il diffracte toute
la lumière dans son ordre utile, l’ordre 1 en général.
b) composant imaginaire appelé réseau blazé en
indice. Le réseau n’a pas de relief ; il est simplement
modulé en indice et cette modulation est un gradient
d’indice parallèle au substrat.
c) approximation binaire d’un composant blazé en
indice.

2
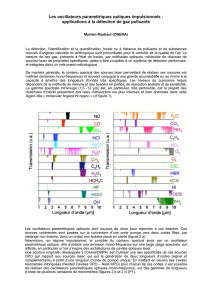
Réseaux blazés binaires : état de l’art en 2000
Nos composants sont parmi les tout premiers et détiennent actuellement les records d'efficacité de
diffraction dans le domaine résonnant, comme en témoignent les figures ci-dessous.
Efficacités de réseaux blazés binaires réalisés
dans différents laboratoires autres que
l’IOTA.
(1-2) : Cornell University, OL 20, 121 (1995),
OL 21, 177 (1996).
(3) : Sandia Lab. OL 20, 1441 (1995).
( ???) : US Army, Caltech OL 25, 381 (2000),
bizarrement, l’efficacité n’est pas donnée
dans l’article.
Comparaison entre les réseaux blazés
binaires et les réseaux blazés échelette. Les
efficacités sont données en lumière non
polarisée, pour une incidence normale et en
transmission.
Résultats expérimentaux dans le visible:
triangles : réseaux IOTA-LMM.
+ : réseaux blazés échelette obtenus par
écriture laser par l’équipe du CSEM [Appl.
Opt. 37, 4069 (1998)].
o : réseaux blazés échelette fabriqués par
écriture électronique (Japonais en 1982 et
Finlandais en 1999)
Résultats théoriques :
Courbe en trait continu : efficacité des
réseaux blazés échelette gravés dans du
verre (le profil triangulaire est idéal)
Il apparaît que :
• si on ne compare que les résultats expérimentaux entre eux, les réseaux blazés binaires offrent
de meilleures efficacités tant que la période Λ est plus petite que 20λ.
• Si on compare nos résultats expérimentaux avec des résultats issus d’un calcul
électromagnétique (le profil triangulaire est supposé parfait), , les réseaux blazés binaires
offrent de meilleures efficacités tant que la période Λ est plus petite que 5λ (angle de déviation
dans l’ordre 1 supérieur à 11°).
Aux grandes périodes, les résultats expérimentaux obtenus pour les réseaux blazés binaires ne
sont pas concluants. Ceci est dû à des problèmes de fabrication, notamment comme le montre des
résultats de tests interférométriques, la taille des piliers fabriqués s’écarte sensiblement de leur taille
nominale. Il est clair que échantillonner une phase lentement variable avec des motifs sub-λ n’est pas
une solution naturelle et représente un challenge technologique dans le visible.
550 600 650 700 750 800 850 900 950 1000 1050 1100
50
55
60
65
70
75
80
85
90
95
100
(3)
(2)
(1)
(???)
o : composant sensible à la polarisation
x : composant "insensible" à la polarisation
longueur d'onde (nm)
efficacité
100101102
40
50
60
70
80
90
100
Λ / λ
Efficacité (%)

3
Effet de guidage : “réseau phasé”
Les composants diffractifs blazés à échelette offrent des efficacités de diffraction remarquables quand
les périodes locales sont grandes devant λ. Par contre, dès que les périodes locales sont de l’ordre de
quelques λ (angles de déviation dans l’ordre 1 allant de quelques degrés à quelques dizaines de degrés,
on parle également d'optiques diffractives opérant dans le domaine résonnant), la performance des
optiques blazées chute très sensiblement. A cela deux raisons. La première est d’ordre technique : lors
de l’écriture sous faisceau convergent, il est délicat
de maîtriser simultanément des doses linéairement
variables (profil échelette) et des transitions
abruptes (parois verticales en bord de zone). La
seconde raison est d’ordre fondamental : pour les
petites périodes, la structure à échelette, même
idéale, n’offre pas une efficacité de 100%, c'est-à-
dire qu'elle ne permet pas de dévier toute la lumière
dans son ordre 1. Ce point est illustré de manière
simplifiée par le tracé de rayons sur la figure ci-
dessus.
Ce problème est d’importance car il restreint en pratique l’impact des optiques diffractives aux
seuls composants qui, en quelque sorte, n’interagissent que faiblement avec la lumière : correction des
aberrations géométriques et achromatisation de systèmes optiques ou, plus généralement, synthèse de
composants de mise en forme de faisceaux qui ne dévient que faiblement la lumière. Un des enjeux
majeurs des recherches menées actuellement est de concevoir et fabriquer des composants diffractifs
efficaces dans le domaine résonnant. Nous avons expliqué† pourquoi les
réseaux blazés binaires ne souffraient pas
de ce problème en montrant que les gros
piliers (ceux qui sont placés notamment
dans la zone morte) agissent comme des
guides d’onde verticaux qui confinent le
champ et canalisent le flux d’énergie lors
de la traversée du réseau. Ce point est
illustré sur la figure ci-contre qui
représente (en niveau de gris) le champ
magnétique dans un réseau constitué de 4
piliers. Il apparaît dans les deux piliers
de droite des ventres et des nœuds de
champ qui correspondent à la présence
d’ondes stationnaires. La distance entre
deux nœuds est typiquement λ/2/neff. Le
vecteur de Poynting représenté par de
petites flèches blanches est relativement
vertical, ce qui atteste que l’effet de
guidage canalise le flux d’énergie et réduit, ou même annule, l’effet d’ombrage. A notre avis, ce
phénomène est intrinsèque aux structures de dimension légèrement sub-λ et est particulièrement
important dans des matériaux de fort indice comme le TiO2 que nous utilisons pour nos réalisations
dans le visible. Cet effet devrait être accentué dans l’infrarouge avec des matériaux semiconducteurs.
† Ph. Lalanne, "Waveguiding in blazed-binary diffractive elements", J.Opt. Soc. Am. A 16, 2517-2520 (1999).
zone morte
onde plane incidente
direction ordre 1

4
Tenue à l’incidence des optiques blazées binaires
A l’effet de guidage précédent peut être donnée une autre interprétation. Eclairé par une onde laser
spatialement cohérente, l’ensemble des petits piliers se comporte comme un ensemble d’émetteurs
cohérents dont la phase est contrôlée par la largeur des piliers. C’est l’équivalent optique des réseaux
phasés des radaristes. Cette image reste valable si l’illumination a une incidence oblique comme le
montre le schéma ci-contre. Par rapport à l’ordre zéro transmis, l’onde transmise par le réseau subit un
déphasage (ψ1, ψ2, ψ3) semblable à celui que subirait une onde en incidence normale. En conséquence,
les réseaux blazés binaires (ou de manière générale,
les optiques blazées binaires) restent efficaces
même pour des incidences fortement obliques.
Nous avons vérifié expérimentalement cette
propriété‡ pour deux réseaux constitués de 3 et 6
piliers et de périodes Λ = 990 nm et 1980 nm. Par
exemple, pour le réseau à 3 piliers, nous avons
observé que l’efficacité (les croix sur la figure ci-
dessous) à 633 nm en lumière non-polarisée est
supérieure à 70% sur un large intervalle angulaire
de plus de 60°. Cette efficacité passe par un
maximum pour sin(θ) ≈ λ/2Λ qui correspond à une
incidence type Littrow. A titre de comparaison, les
efficacités de diffraction théoriques d’un réseau
échelette de même période gravé dans le verre
(courbe en pointillé), et d’un réseau binaire multiniveaux [Noponen et al., AO 31, 5910 (1992)]
composé de 4 marches en escalier optimisées pour maximiser l’efficacité dans l’ordre 1 en incidence
normale (courbe en trait continu) sont représentées.
-80 -60 -40 -20 020
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
blazed-binary
échelette
optimized
m ultilevel
angle (in air)
Efficiency
Expérimentalement, nous avons de plus vérifié que l’efficacité des réseaux blazés binaires est peu
sensible à l’incidence quand le plan d’incidence est perpendiculaire au vecteur réseau. Au bilan, ce
travail suggère que les optiques blazées binaires peuvent être utilisées dans des systèmes d’imagerie
hors axe et/ou avec des champs objet et image importants. De manière plus générale, cette propriété de
tenue à l’incidence qui est unique en optique diffractive, atteste que nos premiers résultats obtenus en
incidence normale ne sont pas fortuits et que l’approche « blazée binaire » est saine.
‡ M.S.L. Lee, Ph. Lalanne and J.C. Rodier, "Wide-field-angle behavior of blazed-binary gratings in the
resonance domain", Opt. Lett. (Déc. 2000).
φ1φ2φ3
ordre zéro
ψ1φ1
+ψ2φ2
+ψ3φ3
+

5
Modélisation des composants blazés binaires synthétisant des fonctions de
phase lentement variables
Cette étude concerne les optiques diffractives de grandes périodes devant la longueur d’onde, c’est-à-
dire dont la phase varie lentement à l’échelle de la longueur d’onde. Les composants concernés sont
très courants : des phases lentement variables se rencontrent par exemple dans les zones centrales des
lentilles diffractives ou dans les optiques hybrides dédiées à la compensation d’aberrations
géométriques ou chromatiques dans les systèmes d’imagerie notamment infrarouge. Dans le visible,
Canon a récemment développé un objectif photo (de focale 400 mm et d’ouverture f/4) qui contient un
élément diffractif multiniveaux.
En optique diffractive classique, les performances de ces composants sont calculées à l’aide de
la théorie scalaire. Dans le cas des structures blazées binaires, on ne peut se contenter de cette
approche car les composants, bien que présentant des phases lentement variables, sont structurés à
l’échelle de λ. Comme dans le domaine résonnant, il faut de fait utiliser la théorie électromagnétique.
Cependant pour des raisons de limitation de mémoire, le cas des optiques blazées binaires de périodes
supérieures à typiquement dix longueurs d’onde ne peut plus être traité. Nous avons donc mis en
œuvre un modèle approché* permettant de prédire les performances (spectrale et angulaire) d’une
optique diffractive blazée binaire dont la fonction de phase quelconque varie lentement à l’échelle de
la longueur d’onde. Ce modèle repose sur des principes physiques simples et utilise à la fois la théorie
électromagnétique et la théorie scalaire. Il exploite notamment la notion de transmittance couramment
utilisée en optique de Fourier. Cette notion est complètement légitime ici car la phase, étant une
fonction lentement variable de λ, localement à l’échelle de plusieurs λ, la structure est équivalente à
un réseau sub-λ qui ne diffracte que dans ses ordres zéro.
Afin de valider ce modèle, nous l’avons confronté à des résultats de calculs
électromagnétiques obtenus pour des réseaux blazés binaires de période croissante. Ces résultats ont
été extrapolés afin d’obtenir la limite de l’efficacité pour des périodes infiniment grandes à l’échelle
de la longueur d’onde (λ/Λ → 0). Nous avons obtenu un très bon accord entre les valeurs extrapolées
et les prédictions du modèle, voir la figure ci-dessous.
Figure : Efficacité de diffraction dans l’ordre
1 de réseaux blazés binaires en fonction du
rapport de la longueur d’onde sur la période.
Les ronds et les croix correspondent
respectivement à une illumination du réseau
en polarisation TM et en polarisation TE. Le
rond et la croix représentés en gras
correspondent aux prédictions de l’efficacité
obtenues à l’aide du modèle (λ/Λ → 0).
Bien qu’il ait été testé pour des réseaux, ce modèle s’applique aux composants blazés binaires
présentant une fonction de phase quelconque. C’est un outil efficace qui devrait permettre d’optimiser
les performances des optiques hybrides conçues avec une approche « blazée binaire ».
* M.S.L. Lee, Ph. Lalanne and P. Chavel, "Blazed-binary diffractive elements with periods much larger than the
wavelength", J. Opt. Soc. Am. A. 17, 1250-1255 (2000).
00.02 0.04 0.06 0.08 0.1
93.5
94
94.5
95
95.5
96
96.5
97
97 5
97
.
5
λ/Λ
c
acité dans l'ordre 1 (%)Effi
c
Prédictions du modèle
Cl l
C
a
l
cu
l
s
électromagnétiques