Lycée Viette TSI 1

Lycée Viette TSI 1
Rabeux Michel Page 1
TD 10 Circuit linéaire ordre 1
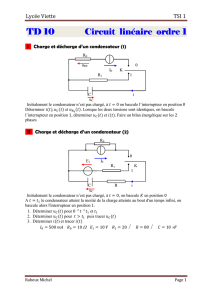
II . Charge et décharge d’un condensateur (1)
R0
uR0 0
I0 K
R1 1
C i
uC
Initialement le condensateur n’est pas chargé, à    on bascule l’interrupteur en position 
Déterminer   et . Lorsque les deux tensions sont identiques, on bascule
l’interrupteur en position , déterminer  et  Faire un bilan énergétique sur les 
phases
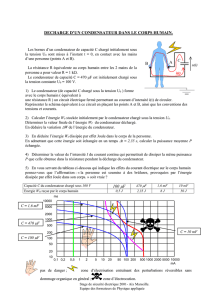
III . Charge et décharge d’un condensateur (2)
R0
0
E1 I0
R1 K
1
C R i
uC
Initialement le condensateur n’est pas chargé, à   , on bascule  en position 
A    le condensateur atteint la moitié de la charge atteinte au bout d'un temps infini, on
bascule alors l'interrupteur en position .
1. Déterminer  pour  et 
2. Déterminer  pour    puis tracer 
3. Déterminer ) et tracer 

Lycée Viette TSI 1
Rabeux Michel Page 2
IIII . Décharge d’un condensateur dans un autre
On relie deux condensateurs de capacités  et , initialement chargés par une résistance .
A    on bascule l'interrupteur. Pour     et   avec   
1. Déterminer et représenter pour    ,  et .
2. Faire un bilan énergétique.
IIV . Oscillations de relaxation
E R
K
C
u
La lampe néon a une résistance infinie à l'extinction et une résistance Rn lorsqu'elle est
allumée. Si la lampe est éteinte et si u croit elle s'allume pour u Ua , puis s'il l'on fait
décroître u, elle s'éteint pour u Ue ( Ue < Ua ). Initialement le condensateur n’est pas chargé.
1. Déterminer u(t) lampe éteinte, t1 instant d'allumage en fonction de E, R, C, Ua
2. Déterminer u(t) pour t > t1 ( lampe allumée ), t2 instant d'extinction en fonction de E, C, Ua,
Ue, Rn, R
3. Déterminer u(t) pour t > t2 ( lampe éteinte ), t3 instant de ré allumage
4. Le phénomène extinction allumage est périodique déterminer la période T
5. Condition sur E pour obtenir ces oscillations de relaxation
6. A.N. E = 120 V Ua = 90 V Ue = 70 V C = 0,1 F N = 2 Hz ( Rn négligé ) Calculer R
IV . Circuit RC et RL
K E
i
i1 R1
i2 R2 C
Initialement le condensateur n’est pas chargé et la bobine n’est parcourue par aucun courant.
A t = 0, on bascule K
Déterminer i1(t) et i2(t), donner la relation entre R1, R2 , C, L pour que i soit indépendant du
temps.

Lycée Viette TSI 1
Rabeux Michel Page 3
IVI . Etablissement du courant dans un circuit
On considère le circuit suivant comportant une bobine idéale d’inductance L et de deux
résistances R et R’. K et K’ sont deux interrupteurs et le générateur de tension possède la
f.e.m E.
1. K’ est ouvert. A l’instant t = 0, on ferme l’interrupteur K.
 Quel est le courant noté I en régime permanent ?
 Déterminer la loi d’évolution de l’intensité i(t).
 Tracer l’allure de la courbe.
2. Le régime permanent d’intensité I est établi (K est fermé depuis longtemps).
A l’instant t = 0, on ferme K’.
 Quelle est la nouvelle intensité I’ en régime permanent.
 Etablir l’équation différentielle régissant l’évolution de i(t).
 Tracer l’allure de i(t).
IVII. Etincelle de rupture
1. Quelle est la valeur de l’intensité i(0) dans le circuit sachant que le courant est établi depuis
longtemps (K fermé) ?
2. On ouvre K à t = 0. Déterminer i(t) et tracer son allure. Que se passe-t-il si R devient très
grande ?
3. Déterminer u(t) et tracer son allure. Que se passe-t-il si R devient très grande ?