Montages à ALI

Montages à ALI page 1/2
MONTAGES A ALI EN FONCTIONNEMENT
LINÉAIRE
VRAI FAUX
L’impédance des entrées d’un ALI sont faibles.
L’impédance de sortie d’un ALI est faible.
Le gain en continu d’un ALI est faible.
La bande passante d’un ALI en boucle ouverte est faible.
Si un ALI est décrit par le modèle idéal, on en déduit V
+
= V
–
On peut écrire la loi des nœuds en un point relié à la masse dans un montage contenant
un ALI.
Il est utile d’écrire la loi des nœuds à la sortie de l’ALI pour en déduire le potentiel de
sortie.
Puisqu’un suiveur réalise V
S
= V
E
, on peut le remplacer sans dommage par un fil.
La fonction de transfert d’un amplificateur inverse ne dépend pas de la fréquence du
signal appliqué.
Le gain en continu d’un amplificateur non inverseur ne dépend pas du gain en continu
µ
0
de l’ALI.
Un montage réalisant la fonction filtrage contient nécessairement au moins un ALI.
Un montage réalisant la fonction filtrage contient nécessairement au moins un
condensateur ou une bobine.
Il y a toujours un dépassement avec un filtre du premier ordre.
Il y a toujours un dépassement avec un filtre du deuxième ordre.
La pulsation de coupure à –3dB est telle que la valeur du gain y est égale à la valeur
maximale du gain divisé par
2
.
Le domaine de variation de la phase d’un filtre du premier ordre est [0, π]
Les asymptotes d’un filtre passe-bande du deuxième ordre ont une pente de –40dB par
décade.
Un filtre passe-bas se comporte comme un dérivateur à hautes fréquences.
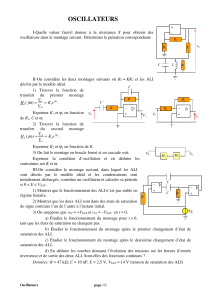
I-Dans le circuit suivant, la résistance
R
1
est fixée. Déterminer R
2
de manière qu’en
valeur absolue, le gain soit le même lorsque
le point A ou le point B sont respectivement
à la masse. Quelle est la valeur de ce gain ?
L’ALI est décrit par le modèle idéal.
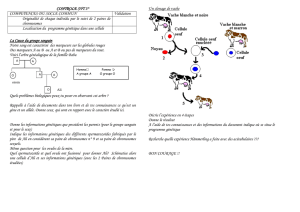
II-Le montage ci-contre est une
source de courant commandée par une
tension constante .
1) L’ALI étant décrit par le modèle idéal, trouver la relation
i
S
= f(v
E
).
2) On suppose maintenant que le gain de l’ALI est réel mais fini
de valeur µ
0
(gain en continu dans le modèle du premier ordre de l’ALI).
a) Exprimer v
S
sous la forme
(
)
S S E
v ki f v
= + .
b) En déduire la résistance de sortie du montage. Conclusion ?
–
+
R
1
R
2
R
U
v
S
i
S
v
E
A
B
R
R
R’
R’
R
1
R
2
–
+
v
S
v
E
A
B

Montages à ALI page 2/2
III-La tension u
E
(t) sinusoïdale est appliquée au filtre suivant:
1) Exprimer la fonction de transfert
harmonique de ce filtre T j
U
U
( )ω =
S
E
2) Tracer l’allure du diagramme de Bode
en amplitude de ce filtre. Quelle est la nature du
filtre et les valeurs numériques de ses
caractéristiques.
Application numérique: on veut que la fréquence de coupure haute soit égale à 2 Hz.
Déterminer C sachant que R = 50 kΩ.
IV-On considère le filtre suivant où l’ALI est décrit par
le modèle idéal de gain infini :
1) Calculer la transmittance H p
V
V
( ) =
S
E
et la mettre sous
la forme canonique suivante:
H p H
mp
mpp
( ) = ×
+ +
F
H
GI
K
J
00
0 0
2
2
12
ω
ω ω
.
Déterminer m, ω0 et H0 en fonction des éléments du circuit.
2) Calculer les pulsations ωA, ωB (avec ωB > ωA) telles que: H j H j H ( ) ( )ω ω
A B
= =
0
2
en
fonction de m et ω0 ainsi que la bande passante du filtre B=
−
ω
ω
π
B A
2
.
3) Calculer le coefficient de qualité du filtre Q, défini par Q=−
ω
ω ω
0
B
A
ainsi que B en
fonction des éléments du circuit.
V-On décrit un ALI par un modèle dans lequel les courants de polarisation IB+ et IB– sont
considérés comme négligeables et où la tension de sortie vS(t) vérifie, en fonctionnement linéaire,
l’équation différentielle suivante:
τ µ
0 0
dv
t
dt
v t v t v t
SS
(
)
( ) ( ) ( )+ = −
+ −
b
g
où τ0 et µ0 sont des constantes réelles positives.
1) Donner l’expression de la fonction de transfert harmonique de l’ALI seul, H j
V
( )ωε =
S
,
en notant ε = V
+
– V
–
.
2) Tracer l’allure du diagramme de Bode en amplitude pour un ampli-op tel que µ
0
= 10
5
et
τ
0
= 0,1 s.
3) On étudie le montage suivant :
Montrer que la fonction de transfert harmonique du montage
s’écrit H j
G
G
H j
1
11
( )
( )
ω
ω
=
+−. Déterminer G en fonction de R
1
et R
2
.
4) Établir le gain en continu G
C
et la fréquence de coupure ω
C
du montage. Calculer leurs valeurs numériques si R
1
= R
2
.
+
–
+
–
u
1
u
E
R
R
R
R
CC
ALI1 ALI2
u
S
R
2
+
–
R
1
C
v
E
v
S
A
C
R
1
+
–
R
2
v
E
v
S
ε