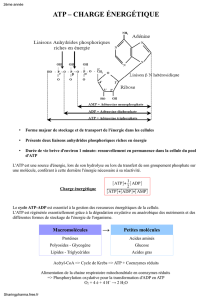
Introduction à l`étude du métabolisme cellulaire : quelques notions

1
Introduction à l'étude du métabolisme cellulaire : quelques notions de thermodynamique,
principaux types de réactions, importance des coenzymes et de l'ATP
Introduction : Un organisme vivant fonctionne en réalisant un ensemble de réactions chimiques intégrées qui
constituent son métabolisme. Ainsi, plus d'un millier de réactions chimiques s'effectuent dans un organisme
aussi simple que la bactérie Escherichia coli.
On peut schématiquement classer les réactions métaboliques en deux grandes catégories :
- les réactions cataboliques qui correspondent aux réactions de dégradation permettant de convertir
l'énergie de molécules source d'énergie en des formes biologiquement utilisables;
- les réactions anaboliques qui regroupent les réactions de synthèse nécessitant un apport d'énergie pour
pouvoir s'effectuer.
Au cours de ces réactions, il y a donc conversion d'une forme d'énergie en une autre. De telles conversions
d'énergie sont décrites par une branche de la physique qui s'appelle la thermodynamique. Le 1er principe de
la thermodynamique par exemple stipule que la quantité d'énergie de l'univers reste constante, et que, par
conséquent, au cours de n'importe quelle transformation physique ou chimique, l'énergie ne peut être ni créée
ni détruite : elle ne peut qu'être convertie d'une forme en une autre.
La bioénergétique, un domaine de la biochimie étudiant les transformations et les utilisations de l’énergie par
les êtres vivants, s’appuie donc sur les principes de la thermodynamique.
Quelles sont les lois de la thermodynamique régissant la réalisation des réactions du métabolisme
cellulaire? Quelles sont les principales réactions impliquées dans le métabolisme cellulaire? Quelles
sont les sources d'énergie utilisées par les cellules? En quelle forme utilisable par les cellules cette
énergie est-elle convertie? Comment s'effectue cette conversion?
L'étude du métabolisme montre que, malgré le très grand nombre de réactions impliquées, on peut tout de
même dégager un schéma général incluant un certain nombre de points communs à toutes ces réactions :
seulement quelques grands types de réactions, l'utilisation d'une unité universelle d'énergie, l'ATP, et
l'apparition d'un nombre limité d'intermédiaires activés, les coenzymes.
Dans la 1ère partie, nous donnerons donc les quelques notions de thermodynamique permettant
d'appréhender ces phénomènes de conversion énergétique, et nous verrons comment ils s'appliquent aux
principaux types de réactions métaboliques. Puis nous montrerons l'organisation de ces réactions
métaboliques au sein d'une cellule en insistant sur le rôle central de l'ATP et des coenzymes.
I. CONDITIONS THERMODYNAMIQUES DE REALISATION DES REACTIONS METABOLIQUES
A. L'enthalpie libre et l'évolution d'un système thermodynamique
1) Les cellules, des systèmes thermodynamiques ouverts
• Un système thermodynamique est une région de l’espace dans laquelle se trouve une certaine quantité de
matière et où s’effectuent des transformations (par exemple une cellule ou un réacteur dans un labo de
chimie). Ce qui est extérieur au système constitue son environnement.
• Les transformations qui s'effectuent dans un système peuvent ou non donner lieu à des échanges avec
l'environnement. On distingue :
- les systèmes ouverts qui échangent de l'énergie et de la matière avec leur environnement;
- les systèmes fermés qui échangent uniquement de l'énergie avec leur environnement;
- les systèmes isolés qui n'échangent ni énergie ni matière avec leur environnement.
• L'énergie d'un système est sa capacité à fournir un travail. Elle s'exprime en J (ou en cal).
1cal=4,18J ou 1J=0,24cal. (1 cal = quantité d'énergie nécessaire pour augmenter la T° d'1g d'eau de 1°C à
25°C)
L'énergie peut être :
- de l'énergie potentielle = énergie qui peut être libérée lors de la survenue de certains processus (par
exemple un déplacement, une réaction entre deux molécules....);
- de l'énergie cinétique = énergie associée à un mouvement;

2
- de la chaleur, qui est une manifestation de l'énergie cinétique liée au mouvement des particules d'un
système.
[1] p 69
Energie potentielle et énergie cinétique sont des formes d'énergie
"utiles" pouvant donner naissance à un travail, contrairement à la
chaleur qui est une forme d'énergie "désordonnée" non utilisable par
les systèmes thermodynamiques (sauf les machines thermiques).
Ainsi, les systèmes biologiques ne peuvent pas utiliser l'énergie
calorique pour réaliser un travail (toutefois, celle-ci augmente
l'agitation moléculaire ce qui facilite les réactions métaboliques  ce
n'est pas tout à fait de l'énergie "perdue"…).
• Une cellule prélève dans son environnement de la matière et de
l'énergie utile grâce à laquelle elle effectue ses travaux, et elle rend à
son environnement des déchets (matière qui ne lui est pas utile), et
des formes dégradées d'énergie (énergie thermique) : c’est un
système thermodynamique ouvert. Les lois de la
thermodynamique s’appliquent normalement aux systèmes fermés
mais on va tout de même pouvoir les transposer aux cellules.
[1] p 67
2) La description des systèmes thermodynamiques
Un système thermodynamique peut être décrit par ses variables d’état : Volume, Masse, Pression,
Température… mais également par ses fonctions d'état = grandeurs thermodynamiques dont la valeur
dépend des variables d'état : énergie interne U, enthalpie H, enthalpie libre G et entropie S.
a) Energie interne et premier principe de la thermodynamique
• L'énergie interne d'un système est définie par U = Q + W où Q est la quantité d'énergie calorique échangée
avec l'extérieur, W le travail fourni.
• Le 1er principe de la thermodynamique stipule que l'énergie interne U de l'univers est constante. Donc
lorsqu'un système subit des transformations, (cad passe d'un état initial i à un état final f), toute variation du
contenu énergétique du système est contrebalancée par une variation symétrique du contenu énergétique de
son environnement.

3
Si une réaction chimique a lieu à P constante (ce qui est le cas dans les cellules), alors Q équivaut à
l’enthalpie H. A P constante, le travail des forces de pression vaut - PΔV.
La variation d'énergie interne d'un système est alors ΔU = ΔH - PΔV.
Dans les cellules, les réactions se font en général à volume constant, et donc ΔU = ΔH.
Dans les systèmes biologiques, la variation d'enthalpie décrit la variation d'énergie interne du système.
Si ΔH>0, le système absorbe de l'énergie (sous forme de chaleur) et la transformation est endergonique.
Si ΔH<0, le système libère de l'énergie (sous forme de chaleur) et la transformation est exergonique.
Cependant, l'étude de la variation d’enthalpie et le 1er principe ne permettent pas de prévoir le sens de
l’évolution d’un système : une réaction spontanée peut être exothermique (ex: combustion de l’essence), ou,
plus rarement, endothermique (ex: dissolution du NaCl)
b) Entropie et deuxième principe de la thermodynamique
• Le 2è principe de la thermodynamique stipule que l'univers se modifie constamment de façon à devenir
plus désordonné.
• L’entropie S mesure le degré d’organisation ou la probabilité de l’existence d’un système :
- plus la distribution des éléments d’un système est aléatoire, plus sa probabilité d'existence est
grande et plus son entropie est élevée;
- au contraire, plus les éléments sont organisés, plus leur probabilité d’existence est petite et plus leur
entropie est faible.
Le niveau 0 de l’entropie correspond à un cristal parfait à la T de 0K.
Le 2è principe, qui signifie que le désordre est plus probable que l'ordre, peut donc s'exprimer de la façon
suivante : l’entropie totale de l’univers augmente (augmentation du degré de désordre) OU la somme des
variations d’entropie d’un système et de son nvironnement est positive : ΔSsystème + ΔSenvironnement > 0.
Un système aura donc tendance à évoluer spontanément vers un état "désordonné" qui va aboutir à une
uniformisation de ses paramètres, c'est-à dire à un état d'équilibre.
Dans cet état d'équilibre, il n'y a plus de travail possible, et donc plus de possibilité de retour spontané à l'état
ordonné. L'énergie interne du système est alors nulle.
• Dans une cellule, les processus
cellulaires vont contribuer à
augmenter l'ordre du système
(ΔS<0, ce qui semble contradictoire
avec le 2è principe), mais cette
diminution de l'entropie est
contrebalancée par une
augmentation encore plus
importante de l'entropie de
l'environnement par libération de
chaleur (ΔS>0).
On aura donc bien ΔSsystème +
ΔSenvironnement > 0.
[1] p 68
L'étude de l'entropie d'un système, et plus particulièrement d'une nouvelle fonction dépendant de S,
l'enthalpie libre G, va donc permettre de prévoir son évolution.

4
3) Les variations d’enthalpie libre et la spontanéité des réactions métaboliques
a) La variation d'enthalpie libre d'un système
• On vient de voir que les transformations subies par un système biologique s'accompagnent en général d'une
libération de chaleur vers son environnement, et donc d'une variation de l'entropie de cet environnement.
Cette variation d'entropie sera plus importante lorsque de la chaleur sera ajoutée à un environnement froid, et
moins importante lorsqu'elle sera ajoutée à un environnement plus chaud.
ΔSenvironnement sera donc proportionnelle à la quantité de chaleur libérée par le système - ΔHsystème, et
inversement proportionnelle à Tenvironnement.
Soit : ΔSenvironnement = - ΔHsystème/T (1)
On sait que : ΔSunivers = ΔSsystème + ΔSenvironnement
En utilisant l'équation (1), on a ΔSunivers = ΔSsystème - ΔHsystème/T
soit : -T.ΔSunivers = ΔHsystème - T.ΔSsystème
-T.ΔSunivers est désignée comme la variation d'énergie libre ou variation d'enthalpie libre (G car elle a été
définie par Gibbs...) : ΔG = ΔH - TΔS
Elle correspond à la fraction de l’énergie récupérable pour la réalisation d’un travail (alors que TΔS représente
la part de l’énergie non disponible pour la réalisation d’un travail).
• Le calcul de la variation d'enthalpie libre d'un système ΔG = Gf-Gi permet donc de prévoir son évolution.
En effet, si les transformations subies par un système sont spontanées, elles vont contribuer à l'augmentation
de l'entropie de l'univers, soit ΔSunivers>0, et donc ΔG<0. Le système évoluera alors spontanément vers son
état d'équilibre qui sera atteint lorsque ΔG=0.
- Si les transformations s'effectuent sans échanges de chaleur, ΔH = 0 et ΔG = -TΔS est bien <0 si l'entropie
du système est augmentée (ΔSsystème>0).
- Si les transformations sont exothermiques, ΔH < 0 et ΔG<0.
- Si les transformations sont endothermiques, ΔH > 0 et, en général, ΔG>0 : les transformations ne sont pas
spontanées. Mais, dans certains cas, TΔS > ΔH et donc ΔG<0 : la transformation est spontanée tout en
étant endothermique. C’est le cas de la dissolution du NaCl dans l’eau, qui s'accompagne d’une forte
augmentation d’entropie du fait du passage de l’état cristallin ordonné à une répartition spatiale aléatoire des
particules en solution.
b) La variation d'enthalpie libre d'une réaction
• Pour étudier les réactions du métabolisme cellulaire, on étudie la variation d’enthalpie libre d’une réaction
(et pas celle d'un système complet) qui permet de prévoir le sens de cette réaction lorsqu'on est à P et T
constantes, ce qui est le cas dans une cellule.
ΔrG = Grf-Gri (mesurée en kJ/mol)
Cette variation dépend uniquement de
l’état final et de l’état initial,
indépendamment du chemin suivi entre ces
deux états. Mais, même si le ΔrG d'une
réaction est <0, le passage de l'état initial à
l'état final peut nécessiter un apport
d'énergie : c'est ce que l'on appelle l'énergie
d'activation de la réaction (qui peut être
fournie par une augmentation de
température par exemple). Les catalyseurs
comme les enzymes ne modifient pas le ΔrG
de la réaction (ils ne peuvent pas rendre
spontanée une réaction qui ne l'est pas),
mais ils abaissent l'énergie d'activation
nécessaire à sa réalisation, ce qui augmente
la vitesse de la réaction. [1] p 73

5
• Si on considère la réaction : A + B C + D on peut définir l’avancement de la réaction.
L’avancement vaut 0 à l'état initial, lorsqu'il n'y a que A et B. Au contraire, l’avancement vaut 1 à l'état final,
lorsqu'il n’y a que C et D.
On peut représenter graphiquement G en fonction de l'avancement de la réaction :
Lorsque G est minimal, la réaction est à
l’équilibre. A "gauche" de l’équilibre, les
concentrations de A et B sont supérieures
à celles de l’équilibre, la réaction de
transformation en C et D a lieu. Et
inversement.
• On peut donc établir un lien entre ΔG et la constante d'équilibre de la réaction.
On peut écrire la variation de G de la façon suivante :
BA
D.
C
.
lnRTGG rr  
avec R=8,306 J.mol-1.K-1
ΔrG dépend de ΔrG° et des concentrations des réactifs dans la cellule, ΔrG° étant la variation d’enthalpie
libre dans les conditions standard.
Les conditions standard correspondent à P=1 atm, T=25°C=298K, concentrations des réactifs en solutions à
1mol/L. (En biologie, on utilise souvent ΔrG°’ avec la condition supplémentaire du pH=7).
A l’équilibre ΔrG=0, on peut donc écrire :
0
e.e
ee
lnRTGG BA
D.
C
rr  
soit
KelnRT
e.e
ee
lnRTGBA
D.
C
r
où Ke est la constante d'équilibre de la réaction.
On peut donc calculer ΔrG° à partir des conditions d’équilibre, ou, inversement, calculer le Ke si on connaît le
ΔrG°
La valeur du ΔrG° donne déjà une indication sur la spontanéité d'une réaction, mais les conditions régnant
dans une cellule n'étant pas standard, le critère de spontanéité d’une réaction est en toute rigueur ΔrG et non
ΔrG°’.
Si ΔrG<0, la réaction est spontanée, de l’énergie est récupérable.
Si ΔrG>0, la réaction est non spontanée, sauf si de l’énergie est apportée.
Si ΔrG=0, la réaction est à l’équilibre, il n’y a ni consommation ni libération d’énergie.
Exemple d'application :
La phosphoglucose isomérase catalyse l’interconversion du glucose 6P (G6P) et du fructose 6P (F6P)
G6P  F6P
Le ΔrG de la réaction s'écrit :
→ A l’équilibre, dans les conditions standard (T = 298K), on observe que [F6P]e/[G6P]e=0,5.
On a alors et ΔrG°=-RTlnKe=+0,41kcal/mol avec R=1,98.10-3kcal/K/mol
G
avancement
0
1
Géquilibre =
Gminimum
eRT
rG
Ke 
.
e
e
lnRTGG P6G
P6F
0r
r 
.
lnRTGG P6G
P6F
rr  