LE CHAMP ÉLECTRIQUE Dans une précédente fiche, après avoir

L’ARPENTEUR DU WEB
CHAMP ÉLECTRIQUE  GUY BOUYRIE
 1 
LE CHAMP ÉLECTRIQUE
Dans une précédente fiche, après avoir introduit les notions de champ scalaire et de champ vectoriel, nous
avons détaillé quelques particularités du champ de pesanteur terrestre. En première S, on attend aussi des
élèves qu’ils soient capables de décrire quelques champs électriques et magnétiques pour certains dispositifs
classiques, conduisant essentiellement à des champs uniformes. L’avantage de l’étude de ces champs est la
facilité avec laquelle on peut obtenir un « spectre », image du champ dans l’espace qui entoure la source.
Les difficultés restent cependant nombreuses car il est difficile d’imaginer un champ électromagnétique et de
comprendre quelle est sa structure. Certes, le programme de première S invite à relier la notion de champ
électromagnétique à quelques objets familiers, comme le téléphone portable ; mais, en Terminale S, quand
on est amené à étudier le mouvement d’une particule chargée dans un champ électrique, on mesure alors
combien cette notion de champ repose sur des acquis bien fragiles, faute d’avoir été suffisamment
« contextualisée ».
Nous allons donc montrer qu’Internet est utile pour illustrer quelques problématiques liées aux « champs
électriques », et aux « champs magnétiques », sur lesquelles s’appuient le programme de première S et bon
nombre de sujets de TPE.
Pour cette première fiche consacrée à un si vaste sujet, nous allons évoquer quelques aspects historiques de
la notion de champ, puis nous allons caractériser un champ électrique électrostatique, avant d’évoquer
quelques champs électriques naturels ou engendrés par des activités techniques humaines.
L’étude des champs magnétiques, et en particulier du champ magnétique terrestre, fera l’objet d’une autre
fiche.
1. LE CHAMP ÉLECTROMAGNÉTIQUE : FONDEMENTS HISTORIQUES
1.1. De FARADAY à MAXWELL
La notion de champ s’est imposée en sciences physiques à partir du moment où l’on a compris le lien qui
pouvait unir le magnétisme à l’électrocinétique. Il revient à FARADAY d’avoir postulé l’existence d’un
champ dans l’espace qui entoure une « source de champ »,
de sorte que l’état physique de cet espace est modifié. Un
corps d’épreuve placé en un point de cet espace ressentira
une force à distance, qui est la preuve que quelque chose
préexistait dans cet espace avant l’introduction du corps.
FARADAY fait alors appel aussi bien à la notion de « ligne
de force » qu’à celle de « ligne de champ ». Ses ouvrages
fondamentaux qui traitent de l’électricité et du magnétisme
sont consultables sur la bibliothèque numérique GALLICA.
Le lien suivant :
http://gallica.bnf.fr/ark:/12148/bpt6k948856/f150.image.r=magnet
ic%20field.langFR
renvoie à une des premières fois où FARADAY évoque
l’existence d’un champ (ou « field »).
La notion de champ va alors s’imposer progressivement
pour permettre d’unifier les différentes interactions, pour
commencer l’interaction électromagnétique. C’est le défi
majeur que s’est fixé FARADAY pour une bonne
compréhension de ces phénomènes.
« I have long held an opinion, almost amounting to
conviction, in common I believe with many other lovers of
natural knowledge, that the various forms under which the
forces of matter are made manifest have one common
origin », écrit en particulier FARADAY en préambule de son
ouvrage.
C’est ensuite MAXWELL qui est capable de donner un contenu mathématique à cette notion de champ
électromagnétique, avec le succès que nous savons.
http://gallica.bnf.fr/ark:/12148/bpt6k91981c.r=Maxwqell.langFR
Figure 1 : l’ouvrage majeur de FARADAY
consacré à l’électricité
http://gallica.bnf.fr/ark:/12148/bpt6k948856.r=faraday.langFR

L’ARPENTEUR DU WEB
CHAMP ÉLECTRIQUE  GUY BOUYRIE
 2 
1.2. La notion de champ : un point de vue unique ? Le regard de Richard FEYNMAN
Ce texte est tiré d’une conférence qui fut donnée en 1965 par Richard FEYNMAN, en partie reproduite sur le
monumental site consacré à Ampère par le CNRS.
http://www.ampere.cnrs.fr/parcourspedagogique/zoom/courant/theorie/index.php
« Les lois physiques ont une nature si délicate que leurs divers énoncés, bien qu’équivalents, ont des
caractères qualitativement très différents ; c’est ce qui en fait l’intérêt. Pour illustrer cela, je vais énoncer la
loi de la gravitation de trois façons, toutes les trois parfaitement équivalentes mais d’apparence
complètement différentes ».
La loi de la gravitation est le plus souvent formulée selon la loi de Newton F = G m1  m2 / r 2.
FEYNMAN en souligne le caractère “non local”, puisqu’il s’agit d’une loi d’action à distance entre deux
corps. Il ajoute : « vous pouvez ne pas aimer l’idée d’une action à distance. Comment cet objet-ci peut-il
savoir ce qui se passe là-bas ? Il y a donc une autre méthode assez étrange, pour énoncer la loi, celle du
champ. Ce deuxième énoncé est local à la fois dans le temps et dans l’espace, car il ne repose que sur ce qui
se passe dans le voisinage de la masse ponctuelle étudiée. Mais les deux énoncés sont mathématiquement
exactement équivalents. »
Enfin FEYNMAN décrit une troisième façon d’énoncer la loi de la gravitation, en exprimant que le
mouvement d’une particule soumise à des forces gravitationnelles est déterminé par un “principe de
minimum” : ce mouvement s’effectue selon un chemin qui minimise une certaine grandeur mathématique.
Avec cette méthode, « nous avons perdu l’idée de causalité, suivant laquelle la particule sent la force et se
déplace sous son influence ». Tout se passe comme si la particule avait exploré tous les chemins possibles et
choisi, après calcul, celui pour lequel la grandeur est minimale.
Et FEYNMAN de conclure : « on peut se demander quelle est la bonne description. Si ces diverses possibilités
ne sont pas exactement équivalentes, si elles entraînent des conséquences différentes, alors il suffira de faire
des expériences pour trouver comment la nature choisit de s’y prendre en fait. Mais dans le cas présent, les
théories sont exactement équivalentes. Mathématiquement, les trois formulations, la loi de Newton, la
méthode du champ local et le principe de minimum, donnent exactement les mêmes conséquences. Il est
impossible de trancher. Mais psychologiquement, il y a une grosse différence entre elles, pour deux raisons.
D’abord, vous pouvez philosophiquement les aimer ou non. Ensuite et surtout elles ne sont pas du tout
équivalentes quand vous essayez de découvrir de nouvelles lois. »
Figure 2 : portail du site consacré à AMPÈRE et à l’histoire de l’électricité
http://www.ampere.cnrs.fr/parcourspedagogique/?lang=fr

L’ARPENTEUR DU WEB
CHAMP ÉLECTRIQUE  GUY BOUYRIE
 3 
Voyons maintenant, à notre époque, comment cette notion de champ, ici électrique, est présentée au grand
public quand on consulte INTERNET.
Voici un site qui est bien indexé par GOOGLE : http://www.clefdeschamps.info/Qu-est-ce-qu-un-champ
Ce site pour néophytes, d’une approche assez agréable, fait un effort pédagogique pour présenter la notion de
« champ » dont on donne plus à connaître les nuisances et les impacts sur la santé humaine (rayonnements
indésirables par les appareils électroménagers, par les antennes des téléphones portables, etc.), que les
fondements théoriques !
Ce site permet donc d’introduire auprès des élèves la notion de champ électromagnétique « en liaison avec
des objets familiers » comme le préconise le programme de première S, avec les préoccupations du moment
sur la santé publique et les « principes de précaution » !
Nous aborderons brièvement en fin d’article les caractéristiques de ces champs électromagnétiques des
réseaux domestiques et leurs conséquences sur la santé humaine.
Figure 3 : la clé des champs
http://www.clefdeschamps.info/Qu-est-ce-qu-un-champ

L’ARPENTEUR DU WEB
CHAMP ÉLECTRIQUE  GUY BOUYRIE
 4 
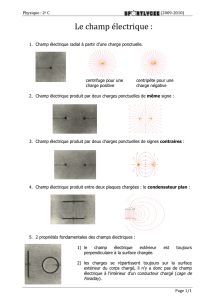
2. LE CHAMP ÉLECTROSTATIQUE E
⟶
En classe de première S, la notion de champ électrostatique E
⟶ en un point de l’espace et celle qui lui est
associée, de potentiel électrique V (sachant que E
⟶ =  grad
⟶
V) est introduite avec des dispositifs classiques :
 Condensateurs plan ou cylindriques dont les armatures sont portées à une différence de potentiel maintenue
aux bornes d’une machine électrostatique (comme la célèbre machine de Whimshurst).
http://www.sciences.univ-nantes.fr/sites/jacques_charrier/tp/wimshurst/wimshurst.html
http://www.youtube.com/watch?v=Zilvl9tS0Og
Ces dispositifs, pourvu que l’on verse une huile isolante dans une cuve placée entre les armatures des
condensateurs et à la surface de laquelle peuvent se déplacer des graines légères, véritables « dipôles
électriques », permettent de cartographier les lignes de champ dans la zone explorée.
 Cuves rhéographiques, comportant deux électrodes portées à une faible différence de potentiel et une
solution conductrice (en général de sulfate de cuivre diluée) pour explorer, avec un contrôleur muni de ses
cordons à pointe de touches, les réseaux d’équipotentielles en leur sein.
Plusieurs sites, réalisés souvent par des collègues, proposent des films de certaines de ces expériences que
tout professeur de sciences physiques en lycée a sans doute réalisées.
Au hasard de nos promenades sur le WEB :
http://machine-wimshurst.e-monsite.com/pages/experiences/le-pendule.html
http://www.web-sciences.com/documents/premiere/pedo13/petp1304.php
http://www.youtube.com/watch?v=q5CZxjp0q7s
 Le Palais de la découverte et ses générateurs électrostatiques (machines de Felici, etc.) reste un « must »
incontournable pour illustrer de façon très spectaculaire la notion de champ électrostatique.
http://www.palais-decouverte.fr/index.php?id=1734
Une conférence du palais de la découverte sur Canal-U :
http://www.canal-u.tv/video/science_en_cours/electrostatique_2003.98
 De très belles expériences d’électrostatique entre autres, au lycée Pissarro de Pontoise.
http://cpge.pissarro.free.fr/VideosPhysique/
Figure 4 : cartographie d’un champ électrostatique uniforme dans un condensateur plan
http://www.web-sciences.com/documents/premiere/pedo13/petp1304.php

L’ARPENTEUR DU WEB
CHAMP ÉLECTRIQUE  GUY BOUYRIE
 5 
3. LIGNES DE CHAMP ET ÉQUIPOTENTIELLES ÉLECTRIQUES
3.1. Observations et définitions
On définit en un point de l’espace proche d’un corps électrisé un « champ électrique » ou un « potentiel
électrique » tout comme au voisinage de la Terre on a défini un « champ de pesanteur » et un « potentiel de
pesanteur ».
1) Une charge test q se trouvant en un point M de l’espace où règne un champ électrique E
⟶ (dont la source
est un corps chargé) peut subir une force électrique F
⟶ telle que : E ⟶ = F
⟶
q .
2) Au point M existe un potentiel électrique V, tout comme il existe un potentiel de pesanteur en un point M
d’un relief par lequel passe une « courbe de niveau » dite « équipotentielle de pesanteur ».
De même que la direction de la force de pesanteur est perpendiculaire à la ligne équipotentielle de pesanteur,
de même la direction de la force électrique exercée sur une charge test, et donc le champ électrique lui-
même, sont perpendiculaires aux lignes équipotentielles électriques.
3) Avec une cuve rhéographique, on met en évidence les lignes équipotentielles électriques, analogues aux
courbes de niveau. Comme les lignes de champ sont en tous points perpendiculaires aux lignes
équipotentielles, une détermination de la configuration des lignes équipotentielles nous permet d’en déduire
celle des lignes de champ électrique.
4) On peut aussi cartographier le champ électrique d’un condensateur avec une machine électrique :
5) À l’intérieur d’un condensateur plan, les lignes de champ sont perpendiculaires aux plaques alors que les
lignes équipotentielles électriques sont parallèles aux plaques (elles sont étagées par « potentiel
décroissant »). Entre les électrodes d’un condensateur cylindrique, les lignes de champ sont radiales alors
que les lignes équipotentielles sont des cercles concentriques. Remarquons qu’à l’intérieur de l’électrode de
rayon le plus faible, le potentiel électrique est constant et le champ électrique est nul : dans cette zone, les
graines ne subissent aucune force électrique (on dit que c’est une « cage de Faraday »).
La relation entre la valeur du champ électrique et du potentiel électrique est de la forme :
 pour le condensateur plan, E = V P  V N
d PN ; P est la plaque chargée « positivement » portée au potentiel
électrique V P le plus haut, alors que N est la plaque chargée « négativement », portée au potentiel électrique
le plus bas. d PN est la distance entre les plaques.
On dit que ce champ est uniforme.
 pour le condensateur cylindrique, E = 
V
r , si
V est la variation du potentiel électrique quand on se
déplace sur une même direction radiale d’une distance qui vaut
r. Si r > 0, V < 0, car la valeur du
potentiel électrique V diminue quand la distance r au centre du dispositif augmente.
 Le champ électrique E
⟶ pointe toujours dans le sens des potentiels décroissants et son intensité s’exprime
en V  m  1 (ou encore en N  C  1).
Fig. 5 : champ électrique d’un condensateur plan
Fig. 6 : champ dans un condensateur cylindrique