Page 1 sur 2 Partie 1 - leprof

Page 1 sur 2
Partie 1 :
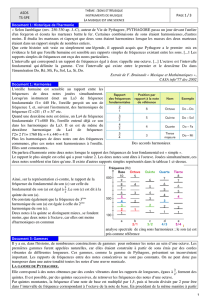
1.1- . Les différents harmoniques d’une fondamentale en musique (appelé premier harmonique en sciences)
sont des multiples par des entiers (k = 2, 3…) de la fondamentale. L’oreille est sensible à la présence
d’harmoniques communs dans différentes notes, ce qui implique des rapports fractionnaires simples (Doc. 1).
1.2- D’après le document 1, l’oreille est plus sensible pour les consonances notées 1/2 (qui donne l’intervalle
d’octave) et 2/3 (qui donne l’intervalle de quinte).
2.1- Une gamme chromatique est une gamme formée de 12 notes.
2.2- La gamme tempérée est une gamme chromatique dans laquelle les 12 notes sont séparées en 12 intervalles
égaux.
3- La hauteur de référence aujourd’hui utilisée en musique est le la3 qui correspond à une fréquence de 440 Hz
4- On donne le même nom à deux notes séparées d’une ou plusieurs octaves car la consonance entre ces notes
est maximale.
5.1- L’intervalle entre deux notes est le rapport entre leur hauteur (fréquence du premier harmonique).
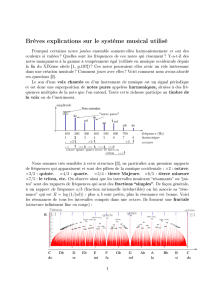
L’intervalle entre deux notes varie dans la gamme de Pythagore. Exemple : d’après le document 2 : entre les
deux premières notes (do et do#) : le rapport vaut 1,067 9, puis entre do# et ré (troisième note de la liste) : le
rapport vaut 1,053
5.2- La courbe du document 2 traduit la construction de la gamme de Pythagore par quinte. Le rapport de
fréquence entre deux notes successivement reliées sur le graphe vaut 3/2 ou 2/3.
6.1- Par définition dans la gamme tempérée, l’écart entre deux notes est constant.
6.2- Chaque note dans la gamme tempérée est séparée de la précédente par un demi-ton. Pour obtenir la
fréquence de la note suivante, il suffit de multiplier la fréquence de la précédente par un facteur 21/12 (soit
1,0595 environ).
7.1- D’après le document 4, le la3 baroque est séparé du la3 standard par un demi-ton environ.
7.2- Le la3 baroque est donc dans la gamme standard un sol#3.
8- Pour construire une gamme en musique, il faut choisir une série de notes classées selon leur fréquence.
9- Une gamme en musique doit à la fois respecter au mieux les consonances, posséder un nombre de notes
limité et permettre des transpositions instrumentales simples.
Partie 2 :
1- Le rapport de fréquences de deux notes séparées d’une octave est égal à deux ; pour deux notes séparées par
une quinte, le rapport est égal à 3/2 ; pour deux notes séparées par une tierce majeure, il est égal à 5/4.
2.1- Une note à la quinte occupe la cinquième position par rapport à une note de référence. D’après le tableau,
la note à la quinte d’un Do est un Sol.
2.2- La note à la quinte d’un Do de fréquence f(Do) = 100 Hz a une fréquence f = 1,5×f(Do) = 150 Hz ;
d’après le tableau du document 7, cette fréquence correspond à un Sol. La note à la quinte du Sol de fréquence
f(Sol) = 150 Hz a une fréquence f = 1,5×f(Sol) = 225 Hz. On divise par 2 cette fréquence pour la ramener dans
l’octave (100 Hz < f < 200 Hz). On obtient une valeur de 112,5 Hz, qui est un Ré. La note à la quinte du Ré de
fréquence f(Ré) = 112,5 Hz a une fréquence f = 1,5×f(Ré) = 168,8 Hz ; c’est un La. La note à la quinte du La
de fréquence f(La) = 168,8 Hz a une fréquence f = 1,5×f(La) = 253,1 Hz. On divise par 2 la valeur exacte de
cette fréquence pour la ramener dans l’octave. On obtient une valeur de 126,6 Hz, qui est un Mi. La note à la
quinte du Mi de fréquence f(Mi) = 126,6 Hz a une fréquence f = 1,5×f(Mi) = 189,8 Hz ; c’est un Si. On
obtient la fréquence du Fa par quinte descendante : f(Fa) = (f(Do)/1,5) × 2 = 133,3 Hz.
3- La gamme tempérée contient 12 demi-tons. Le rapport de fréquences entre deux demi-tons consécutifs est
de
12 2
.
4- Un son harmonieux est constitué de notes dont les rapports de fréquences sont simples. Par exemple,
lorsque le rapport de fréquences entre deux notes est égal à deux, la combinaison de ces notes est agréable à
l’oreille.
La gamme : science et musique
Activité
Documentaire 0

Page 2 sur 2
5- Deux exemples de réponses :
• accord (Do, Sol, Ré) :
Les notes sont séparées deux à deux par une quinte.
)f(Do
)f(Sol
3
3
=
61,632
392,00
= 1,5 et
)f(Sol
)f(ré
3
4
=
92,003
587,33
= 1,5 ;
• accord (Do, Mi, Sol) :
Le Do et le Mi sont à la tierce l’un de l’autre.
)f(Do
)f(Mi
3
3
=
61,632
329,63
= 1,26 et 5/4 = 1,25
Le Do et le Sol sont à la quinte l’un de l’autre.
)f(Do
)f(Sol
3
3
=
61,632
392,00
= 1,5
6- La musique peut être considérée comme une discipline scientifique, car les notes sont caractérisées par
leurs fréquences. Les fréquences des notes de la gamme tempérée ou de la gamme de Pythagore sont calculées
les unes par rapport aux autres. De même, un son harmonieux est constitué de notes dont les rapports de
fréquences sont simples (octave, quinte, tierce, etc.).