ASDS musique sciencecor

!
1!
ASDS$
TS&SPE$
THÈME$:$SONS$ET$MUSIQUE$
INSTRUMENTS$DE$MUSIQUE$
LA$MUSIQUE$EST$UNE$SCIENCE$$
PAGE$1$/$3$
Document)1:)Historique)de)l'harmonie)))
« Selon Jamblique (env. 250-330 ap. J.-C), auteur de Vie de Pythagore, PYTHAGORE passa un jour devant l'atelier
d'un forgeron et écouta les marteaux battre le fer. Certaines combinaisons de sons étaient harmonieuses, d'autres
moins. Il étudia les marteaux et s'aperçut que deux sons étaient harmonieux lorsque les masses des deux marteaux
étaient dans un rapport simple de nombres entiers.
Que cette histoire soit vraie ou simplement une légende, il apparaît acquis que Pythagore a le premier mis en
évidence le fait que l'oreille humaine est sensible aux rapports simples de fréquences existant entre les sons. [...1 Les
rapports simples de fréquences ont reçu des noms particuliers.
L'intervalle qui correspond à un rapport de fréquences égal à deux s'appelle une octave. [...] L'octave est l'intervalle
fondamental qui délimite la gamme. C'est l'intervalle qui existe entre le premier et le deuxième Do dans
l'énumération Do, Ré, Mi, Fa, Sol, La, Si, Do.
Extrait de F. Bruinault « Musique et Mathématiques »,
CASA info°77 dec.2002
Document)1:)Harmonies)
L'oreille humaine est sensible au rapport entre les
fréquences de deux notes jouées simultanément.
Lorsqu'un instrument émet un La3 de fréquence
fondamentale f1= 440 Hz, l'oreille perçoit un son de
fréquence f, et, suivant l'instrument, des harmoniques de
fréquence f2 =2f1 ; f3 = 3f" etc.
Quand une deuxième note est émise, un La4 de fréquence
fondamentale f’1=880 Hz, l'oreille entend déjà ce son
dans les harmoniques du La3. Il en est de même du
deuxième harmonique du La4 de fréquence:
f'2= 2 f'1= 1760 Hz = 4 x 440 = 4 f1
Plus les harmoniques de deux notes ont des fréquences
communes, plus ces notes sont harmonieuses à l'oreille.
Elles sont consonantes.
Des accords harmonieux
On parlera d'harmonie entre deux notes lorsque le rapport des fréquences de leur fondamental est « simple ».
Le rapport le plus simple est celui qui a pour valeur 2. Les deux notes sont dites à l'octave. Jouées simultanément, ces
deux notes semblent n'en faire qu'une. Il existe d'autres rapports simples représentés dans le tableau 1 ci-dessus. !
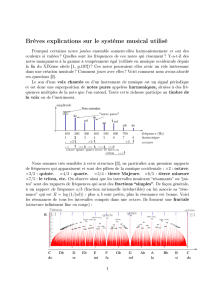
Ainsi, sur la représentation ci-contre, le rapport de la
fréquence du fondamental du son (c) sur celle du
fondamental du son (a) est égal à !
! .Le son (c) est dit à la
quinte du son (a).
On constate également que la fréquence du 3ème
harmonique du son (a) est égale à celle du 2ème
harmonique du son (c).
Deux notes à la quinte se distinguent mieux, se fondent
moins, que deux notes à l'octave, car elles ont moins
d'harmoniques en commun
analyse spectrale de cinq sons harmonieux ; le son (a) est
pris comme référence
Document)3:)Gammes)
Il y a eu, dans l'histoire, de nombreuses constructions de gammes pour ordonner les notes au sein d’une octave. Les
premières gammes furent appelées naturelles, car elles étaient construite à partir de sons émis par des cordes
vibrantes de différentes longueurs. Ces gammes, comme la gamme de Pythagore, présentent un inconvénient
important. Les rapports de fréquences entre des notes consécutives ne sont pas constants. On ne peut donc pas
transposer dans une autre tonalité toutes les notes d’une œuvre musicale.
LA GAMME DE PYTHAGORE.
Elle correspond à des notes obtenues par des cordes vibrantes dont les rapports de longueurs, égaux à !
!, forment des
quintes. Il est possible, par des quintes successives, de retrouver les fréquences des notes d’une octave.
Par quintes montantes, la fréquence d’une note de base est multiplié par 1,5, puis si besoin divisée par 2 pour être
dans l’intervalle de fréquence correspondant à l’octave de la note de base. En procédant de la même manière à partir

!
2!
de la note obtenue, on construit une série de notes dont les six premières sont affectées d’un nom simple ( Do, Ré,
Mi, Sol, La , Si) ;
- par quintes descendantes, la fréquence d’une note de base est divisée par 1,5, puis si besoin multipliée par deux
pour être dans l’intervalle de fréquences correspondant à l’octave. En procédant de la même manière à partir de la
note obtenue, on construit une autre série de notes dont la première est affectée d’un nom simple (Fa).
Les autres notes de l’octave sont dites altérées, et notées dièse (♯) ou bémol (♭). Elles ne sont pas conservées si
leurs fréquences sont trop proches, les unes des autres. Le tableau ci-dessous indiques les rapports des fréquences
entre deux notes non altérées consécutives
LA GAMME TEMPÉRÉE OU À TEMPÉRAMENT ÉGAL
Douze notes sont placées sur une octave qui est alors divisée
en douze intervalle appelés demi-tons. Ces douze notes sont
Do ; Do♯;Ré ;Mi♭; Mi; Fa; Fa♯; Sol; Sol♯;La; Si♭; Si
Le rapport des fréquences entre deux notes consécutives de
fréquence respective f1et f2 est constant
𝑓
!
𝑓
!
=2
!
!"
quelques notes de musique de la gamme tempérées et
leurs fréquences
Questions):))
1) Quel est le rapport de fréquences entre deux notes séparées par :
- une octave :
Le rapport de fréquences de deux notes séparées d’une octave est égal à deux
𝑓
!
𝑓
!
=2
- une quinte
Le rapport de fréquences de deux notes séparées par une quinte, le rapport est égal à
𝑓
!
𝑓
!
=
3
2
- une tierce
Le rapport de fréquences de deux notes séparées par une tierce majeure,
𝑓
!
𝑓
!
=
5
4
2. a) Quelle position occupe une note à la quinte d’une première note dans l’enchaînement Do, Ré, Mi, Fa, Sol, La, Si
Une note à la quinte occupe la cinquième position par rapport à une note de référence. D’après le tableau, la note à
la quinte d’un Do est un Sol.
2.b) Vérifier que le texte et le tableau du document 3 sont en accord
La note à la quinte d’un Do de fréquence 𝑓
!" =100!𝐻𝑧 a une fréquence 𝑓=1,5∙𝑓 !" =150!𝐻𝑧
d’après le tableau du document 3, cette fréquence correspond à un Sol.
La note à la quinte du Sol de fréquence𝑓
!"# =150!𝐻𝑧 a une fréquence 𝑓=1,5∙𝑓 !"# =225!𝐻𝑧
Puisque que la fréquence obtenue est supérieure à l’octave, on divise par 2 cette fréquence pour la ramener dans
l’octave (100 Hz < f < 200 Hz). On obtient une valeur de 𝑓=!!"!
!
=112,5!𝐻𝑧 , qui est un Ré.
La note à la quinte du Ré de fréquence 𝑓
!é=112,5!𝐻𝑧 a une fréquence !𝑓=1,5∙𝑓 !é=1,5×112,5=168,8!𝐻𝑧!;
c’est un La.
La note à la quinte du La de fréquence 𝑓
!" =168,8!𝐻𝑧 a une fréquence 𝑓=1,5∙𝑓 !" =1,5×168,8!=𝐻𝑧!. On
divise par 2 la valeur exacte de cette fréquence pour la ramener dans l’octave. On obtient une valeur de
𝑓=!"#,!!
!
=126,6!𝐻𝑧, qui est un Mi.
La note à la quinte du Mi de fréquence 𝑓
!" =126,6!𝐻𝑧!a une fréquence 𝑓=1,5∙𝑓 !" =1,5× 126,6=189,8!𝐻𝑧!;
c’est un Si.

!
3!
On obtient la fréquence du Fa par quinte descendante après division par 2 pour que la fréquence obtenue soit située
dans l’intervalle de l’octave
𝑓
!" =!!"
!,!
=!""!
!,!
×2=133,3!𝐻𝑧
3) Combien de demi-tons contient une octave de la gamme tempérée ?
La gamme tempérée contient 12 demi-tons.
Quel est le rapport de fréquence entre deux demi-tons consécutifs
Le rapport de fréquences entre deux demi-tons consécutifs est de 2
!"
4) donner une définition historique d’un son harmonieux
Un son harmonieux est constitué de notes dont les rapports de fréquences sont simples. Par exemple, lorsque le
rapport de fréquences entre deux notes est égal à deux, la combinaison de ces notes est agréable à l’oreille.
5) Proposer plusieurs accords harmonieux avec trois notes de la gamme tempérée
• accord (Do, Sol, Ré) :
les notes sont séparées deux à deux par une quinte.
En effet :
𝑓
!"#!!
𝑓
!"!!
!=
392,00
261,63
=1,5=!
3
2
𝑓
!é!!
𝑓
!"#!!
!=
587,33
392,00
=1,5=!
3
2
• accord (Do, Mi, Sol) :
le Do et le Mi sont à la tierce l’un de l’autre et le Do et le Sol sont à la quinte l’un de l’autre.
Do et le Mi sont à la tierce l’un de l’autre
𝑓
!"!!
𝑓
!"!!
!=
329,63
261,63
=1,26 =!
5
4
Le Do et le Sol sont à la quinte l’un de l’autre
𝑓
!"#!!
𝑓
!"!!
!=
392,0
261,63
=1,5≈!
3
2
6) Bilan : Expliquer en quelques lignes pourquoi la musique peut être considérée comme une discipline scientifiques
La musique peut être considérée comme une discipline scientifique, car les notes sont caractérisées par leurs
fréquences
Les fréquences des notes de la gamme tempérée ou de la gamme de Pythagore sont calculées les unes par rapport
(mathématiques) aux autres.
De même, un son harmonieux est constitué de notes dont les rapports (mathématiques) de fréquences sont simples
(octave, quinte, tierce, etc.)
$